24.2 与圆有关的位置关系(第4课时)
文档属性
| 名称 | 24.2 与圆有关的位置关系(第4课时) |

|
|
| 格式 | rar | ||
| 文件大小 | 74.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 五四学制版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-20 13:49:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
24.2 与圆有关的位置关系(第4课时) ( http: / / www.21cnjy.com / )
教学内容
1.两个圆相离(外离、内含),两个圆相切(外切、内切),两个圆相交等概念.
2.设两圆的半径分别为r1、r2,圆心距(两圆圆心的距离)为d,则有两圆的位置关系,d与r1和r2之间的关系.
外离d>r1+r2
外切 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 d=r1+r2
相交│r1-r2│内切 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 d=│r1-r2│
内含0≤d<│r1-r2│(其中d=0,两圆同心)
教学目标
了解两个圆相离(外离、内含),两个圆相切(外切、内切),两圆相交、圆心距等概念.
理解两圆的互解关系与d、r1、r2等量关系的等价条件并灵活应用它们解题.
通知复习直线和圆的位置关系和结合操作几何,迁移到圆与圆之间的五种关系并运用它们解决一些具体的题目.
重难点、关键
1.重点:两个圆的五种位置关系中的等价条件及它们的运用.
2.难点与关键:探索两个圆之间的五种关系的等价条件及应用它们解题.
教学过程
一、复习引入
请同学们独立完成下题.
在你的随堂练习本上,画出直线L和圆的三种位置关系,并写出等价关系.
老师点评:直线L和圆的位置关系有三种:相交、相切、相离,如图(a)~(c)所示.(其中d表示圆心到直线L的距离,r是⊙O的半径)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(a) 相交 dr
二、探索新知
请每位同学完成下面一段话的操作几何,四人一组讨论你能得到什么结论.
(1)在一张透明纸上作一个⊙O1,再在另一张透明纸上作一个与⊙O1半径不等的⊙O2,把两张透明纸叠在一起,固定⊙O1,平移⊙O2,⊙O1与⊙O2有几种位置关系?
(2)设两圆的半径分别为r1和r2(r1老师用两圆在黑板上运动并点评:
可以发现,可以会出现以下五种情况:
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
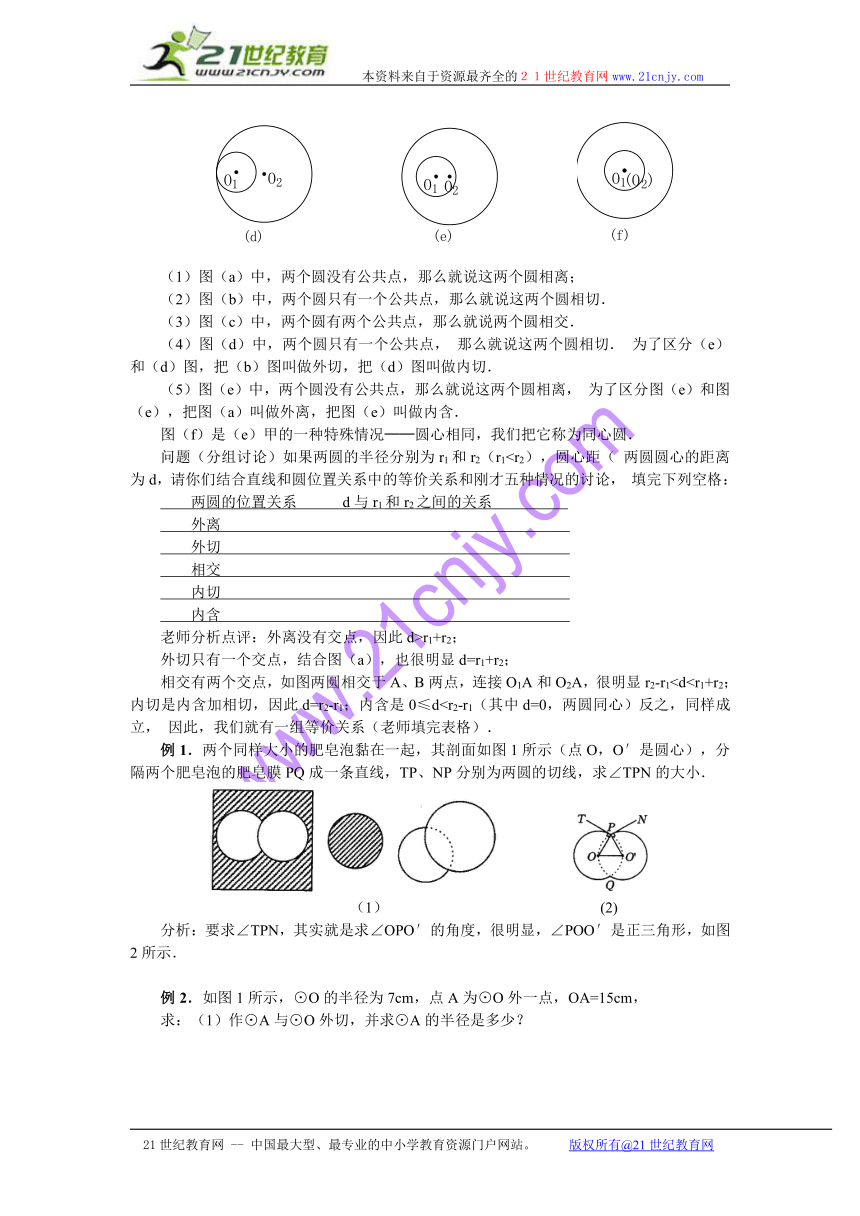
(1)图(a)中,两个圆没有公共点,那么就说这两个圆相离;
(2)图(b)中,两个圆只有一个公共点,那么就说这两个圆相切.
(3)图(c)中,两个圆有两个公共点,那么就说两个圆相交.
(4)图(d)中,两个圆只有一个公共点,那么就说这两个圆相切.为了区分(e)和(d)图,把(b)图叫做外切,把(d)图叫做内切.
(5)图(e)中,两个圆没有公共点,那么就说这两个圆相离,为了区分图(e)和图(e),把图(a)叫做外离,把图(e)叫做内含.
图(f)是(e)甲的一种特殊情况──圆心相同,我们把它称为同心圆.
问题(分组讨论)如果两圆的半径分别为r1和r2(r1两圆的位置关系 d与r1和r2之间的关系
外离
外切
相交
内切
内含
老师分析点评:外离没有交点,因此d>r1+r2;
外切只有一个交点,结合图(a),也很明显d=r1+r2;
相交有两个交点,如图两圆相交于A、B两点,连接O1A和O2A,很明显r2-r1例1.两个同样大小的肥皂泡黏在一起,其剖面如图1所示(点O,O′是圆心),分隔两个肥皂泡的肥皂膜PQ成一条直线,TP、NP分别为两圆的切线,求∠TPN的大小.
( http: / / www.21cnjy.com )
(1) (2)
分析:要求∠TPN,其实就是求∠OPO′的角度,很明显,∠POO′是正三角形,如图2所示.
例2.如图1所示,⊙O的半径为7cm,点A为⊙O外一点,OA=15cm,
求:(1)作⊙A与⊙O外切,并求⊙A的半径是多少?
( http: / / www.21cnjy.com )
(1) (2)
(2)作⊙A与⊙O相内切,并求出此时⊙A的半径.
分析:(1)作⊙A和⊙O外切,就是作以A为圆心的圆与⊙O的圆心距d=rO+rA;(2)作OA与⊙O相内切,就是作以A为圆心的圆与⊙O的圆心距d=rA-rO.
解:如图2所示,(1)作法:以A为圆心,rA=15-7=8为半径作圆,则⊙A的半径为8cm
(2)作法:以A点为圆心,rA′=15+7=22为半径作圆,则⊙A的半径为22cm
三、巩固练习
教材P109 练习.
四、应用拓展
例3.如图1所示,半径不等的⊙O1、⊙O2外离,线段O1O2分别交⊙O1、⊙O2于点A、B,MN为两圆的内公切线,分别切⊙O1、⊙O2于点M、N,连结MA、NB.
(1)试判断∠AMN与∠BNM的数量关系?并证明你的结论.
(2)若将“MN”为两圆的内公切线改为“MN为两圆的外公切线”,其余条件不变,∠AMN与∠BNM是否一定满足某种等量关系?完成下图并写出你的结论.
( http: / / www.21cnjy.com )
(1) (2)
分析:(1)要说明∠AMN与∠BNM的数量关系,只要说明∠MAB和∠NBA的数量关系,只要说明∠O2BN和∠O1AM的数量关系,又因为∠O2BN=∠O1NB,∠O1MA=∠O1AM,因此,只要连结O1M,O2N,再说明∠MO1A=∠NO2B,这两个角相等是显然的.
(2)画出图形,从上题的解答我们可以得到一个思路,连结O1M、O2N,则∠O1MN+∠O2NM=180°,∴∠MO1A+∠NO2B=180°,∴∠O2NB+∠O1MA=90°,∴∠AMN+∠BNM=90°.
五、归纳小结(学生归纳,老师点评)
本节课应掌握:
1.圆和圆位置关系的概念:两个圆相离(外离、内含),相切(外切、内切),相交.
2.设两圆的半径为r1,r2,圆心距为d(r1则有:外离 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 d>r1+r2
外切d=r1+r2
相交r2-r1内切d=r2-r1
内含0≤d六、布置作业
1.教材P110 复习巩固6、7 P111 综合运用11、13.
第四课时作业设计
1、 选择题.
1.已知两圆的半径分别为5cm和7cm,圆心距为8cm,那么这两个圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
2.半径为2cm和1cm的⊙O1和⊙O2相交于A、B两点,且O1A⊥O2A,则公共弦AB的长为( ).
A.cm B.cm C.cm D.cm
3.如图所示,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是( ).
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=x2-x
二、填空题.
1.如图1所示,两圆⊙O1与⊙O2相交于A、B两点,则O1O2所在的直线是公共弦AB的________.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3)
2.两圆半径R=5,r=3,则当两圆的圆心距d满足______时,两圆相交;当d满足_______时,两圆不外离.
3.如图2所示,⊙O1和⊙O2内切于T,则T在直线________上,理由是_________________;若过O2的弦AB与⊙O2交于C、D两点,若AC:CD:BD=2:4:3,则⊙O2与⊙O1半径之比为________.
三、综合提高题.
1.如图3,已知⊙O1、⊙O2相交于A、B两点,连结AO1并延长交⊙O1于C,连CB并延长交⊙O2于D,若圆心距O1O2=2,求CD长.
2.如图所示,是2004年5月5日2时48分到3时52分在北京拍摄的从初六到十五的月全食过程.
用数学眼光看图(a),可以认为是地球、月球投影(两个圆)的位置关系发生了从外切、相交到内切的变化;2时48分月球投影开始进入进球投影的黑影(图(b)),接着月球投影沿直线OP匀速的平行移动进入地球投影的黑影(图24-87(c),3时52分,这时月球投影全部进入地球投影的(图(d)),设照片中地球投影如图(2)中半径为R的⊙O,月球投影如图24-87(b)中半径为r的小圆⊙P,这段时间的圆心距为OP=y,求y与时间t(分)的函数关系式,并写出自变量的取值范围.
3.如图所示,点A坐标为(0,3),OA半径为1,点B在x轴上.
(1)若点B坐标为(4,0),⊙B半径为3,试判断⊙A与⊙B位置关系;
(2)若⊙B过M(-2,0)且与⊙A相切,求B点坐标.
课后教学反思:_______________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
________________________________________________________________________________________________________________________________________________________
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
24.2 与圆有关的位置关系(第4课时) ( http: / / www.21cnjy.com / )
教学内容
1.两个圆相离(外离、内含),两个圆相切(外切、内切),两个圆相交等概念.
2.设两圆的半径分别为r1、r2,圆心距(两圆圆心的距离)为d,则有两圆的位置关系,d与r1和r2之间的关系.
外离d>r1+r2
外切 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 d=r1+r2
相交│r1-r2│
内含0≤d<│r1-r2│(其中d=0,两圆同心)
教学目标
了解两个圆相离(外离、内含),两个圆相切(外切、内切),两圆相交、圆心距等概念.
理解两圆的互解关系与d、r1、r2等量关系的等价条件并灵活应用它们解题.
通知复习直线和圆的位置关系和结合操作几何,迁移到圆与圆之间的五种关系并运用它们解决一些具体的题目.
重难点、关键
1.重点:两个圆的五种位置关系中的等价条件及它们的运用.
2.难点与关键:探索两个圆之间的五种关系的等价条件及应用它们解题.
教学过程
一、复习引入
请同学们独立完成下题.
在你的随堂练习本上,画出直线L和圆的三种位置关系,并写出等价关系.
老师点评:直线L和圆的位置关系有三种:相交、相切、相离,如图(a)~(c)所示.(其中d表示圆心到直线L的距离,r是⊙O的半径)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(a) 相交 d
二、探索新知
请每位同学完成下面一段话的操作几何,四人一组讨论你能得到什么结论.
(1)在一张透明纸上作一个⊙O1,再在另一张透明纸上作一个与⊙O1半径不等的⊙O2,把两张透明纸叠在一起,固定⊙O1,平移⊙O2,⊙O1与⊙O2有几种位置关系?
(2)设两圆的半径分别为r1和r2(r1
可以发现,可以会出现以下五种情况:
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)图(a)中,两个圆没有公共点,那么就说这两个圆相离;
(2)图(b)中,两个圆只有一个公共点,那么就说这两个圆相切.
(3)图(c)中,两个圆有两个公共点,那么就说两个圆相交.
(4)图(d)中,两个圆只有一个公共点,那么就说这两个圆相切.为了区分(e)和(d)图,把(b)图叫做外切,把(d)图叫做内切.
(5)图(e)中,两个圆没有公共点,那么就说这两个圆相离,为了区分图(e)和图(e),把图(a)叫做外离,把图(e)叫做内含.
图(f)是(e)甲的一种特殊情况──圆心相同,我们把它称为同心圆.
问题(分组讨论)如果两圆的半径分别为r1和r2(r1
外离
外切
相交
内切
内含
老师分析点评:外离没有交点,因此d>r1+r2;
外切只有一个交点,结合图(a),也很明显d=r1+r2;
相交有两个交点,如图两圆相交于A、B两点,连接O1A和O2A,很明显r2-r1
( http: / / www.21cnjy.com )
(1) (2)
分析:要求∠TPN,其实就是求∠OPO′的角度,很明显,∠POO′是正三角形,如图2所示.
例2.如图1所示,⊙O的半径为7cm,点A为⊙O外一点,OA=15cm,
求:(1)作⊙A与⊙O外切,并求⊙A的半径是多少?
( http: / / www.21cnjy.com )
(1) (2)
(2)作⊙A与⊙O相内切,并求出此时⊙A的半径.
分析:(1)作⊙A和⊙O外切,就是作以A为圆心的圆与⊙O的圆心距d=rO+rA;(2)作OA与⊙O相内切,就是作以A为圆心的圆与⊙O的圆心距d=rA-rO.
解:如图2所示,(1)作法:以A为圆心,rA=15-7=8为半径作圆,则⊙A的半径为8cm
(2)作法:以A点为圆心,rA′=15+7=22为半径作圆,则⊙A的半径为22cm
三、巩固练习
教材P109 练习.
四、应用拓展
例3.如图1所示,半径不等的⊙O1、⊙O2外离,线段O1O2分别交⊙O1、⊙O2于点A、B,MN为两圆的内公切线,分别切⊙O1、⊙O2于点M、N,连结MA、NB.
(1)试判断∠AMN与∠BNM的数量关系?并证明你的结论.
(2)若将“MN”为两圆的内公切线改为“MN为两圆的外公切线”,其余条件不变,∠AMN与∠BNM是否一定满足某种等量关系?完成下图并写出你的结论.
( http: / / www.21cnjy.com )
(1) (2)
分析:(1)要说明∠AMN与∠BNM的数量关系,只要说明∠MAB和∠NBA的数量关系,只要说明∠O2BN和∠O1AM的数量关系,又因为∠O2BN=∠O1NB,∠O1MA=∠O1AM,因此,只要连结O1M,O2N,再说明∠MO1A=∠NO2B,这两个角相等是显然的.
(2)画出图形,从上题的解答我们可以得到一个思路,连结O1M、O2N,则∠O1MN+∠O2NM=180°,∴∠MO1A+∠NO2B=180°,∴∠O2NB+∠O1MA=90°,∴∠AMN+∠BNM=90°.
五、归纳小结(学生归纳,老师点评)
本节课应掌握:
1.圆和圆位置关系的概念:两个圆相离(外离、内含),相切(外切、内切),相交.
2.设两圆的半径为r1,r2,圆心距为d(r1
外切d=r1+r2
相交r2-r1
内含0≤d
1.教材P110 复习巩固6、7 P111 综合运用11、13.
第四课时作业设计
1、 选择题.
1.已知两圆的半径分别为5cm和7cm,圆心距为8cm,那么这两个圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
2.半径为2cm和1cm的⊙O1和⊙O2相交于A、B两点,且O1A⊥O2A,则公共弦AB的长为( ).
A.cm B.cm C.cm D.cm
3.如图所示,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是( ).
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=x2-x
二、填空题.
1.如图1所示,两圆⊙O1与⊙O2相交于A、B两点,则O1O2所在的直线是公共弦AB的________.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3)
2.两圆半径R=5,r=3,则当两圆的圆心距d满足______时,两圆相交;当d满足_______时,两圆不外离.
3.如图2所示,⊙O1和⊙O2内切于T,则T在直线________上,理由是_________________;若过O2的弦AB与⊙O2交于C、D两点,若AC:CD:BD=2:4:3,则⊙O2与⊙O1半径之比为________.
三、综合提高题.
1.如图3,已知⊙O1、⊙O2相交于A、B两点,连结AO1并延长交⊙O1于C,连CB并延长交⊙O2于D,若圆心距O1O2=2,求CD长.
2.如图所示,是2004年5月5日2时48分到3时52分在北京拍摄的从初六到十五的月全食过程.
用数学眼光看图(a),可以认为是地球、月球投影(两个圆)的位置关系发生了从外切、相交到内切的变化;2时48分月球投影开始进入进球投影的黑影(图(b)),接着月球投影沿直线OP匀速的平行移动进入地球投影的黑影(图24-87(c),3时52分,这时月球投影全部进入地球投影的(图(d)),设照片中地球投影如图(2)中半径为R的⊙O,月球投影如图24-87(b)中半径为r的小圆⊙P,这段时间的圆心距为OP=y,求y与时间t(分)的函数关系式,并写出自变量的取值范围.
3.如图所示,点A坐标为(0,3),OA半径为1,点B在x轴上.
(1)若点B坐标为(4,0),⊙B半径为3,试判断⊙A与⊙B位置关系;
(2)若⊙B过M(-2,0)且与⊙A相切,求B点坐标.
课后教学反思:_______________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
________________________________________________________________________________________________________________________________________________________
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
