22.8多边形的内角和与外角和

课件26张PPT。22.8 多边形的内角和与外角和曲周县安寨中学 三角形有三个内角、三条边，我们也可以把三角形称为三边形（但我们习惯称为三角形）． 你能说出三角形的定义吗？三角形是由三条不在同一条直线上的线段
首尾顺次相接组成的平面图形 回忆 ：既然我们已经知道什么叫三角形，你能根据三角形
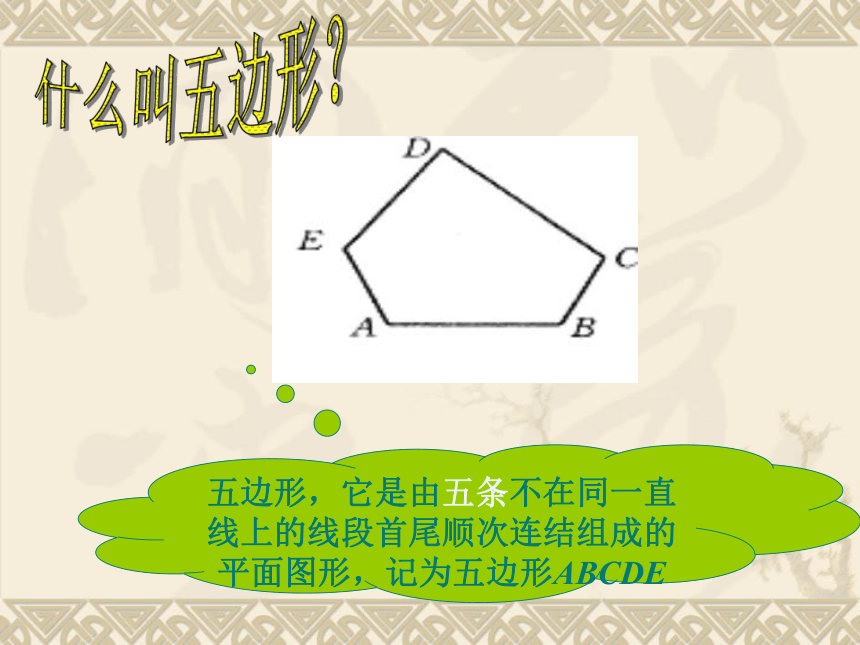
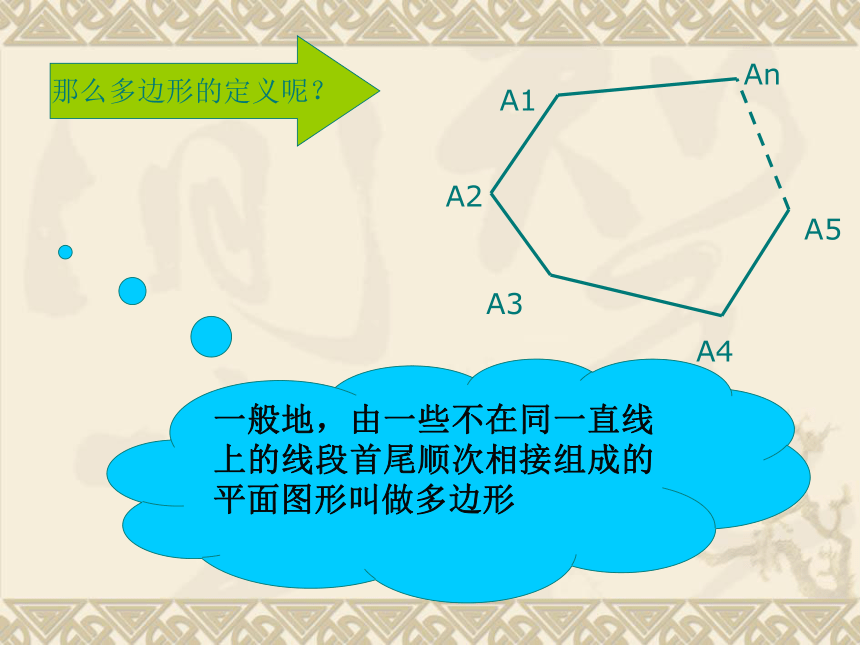
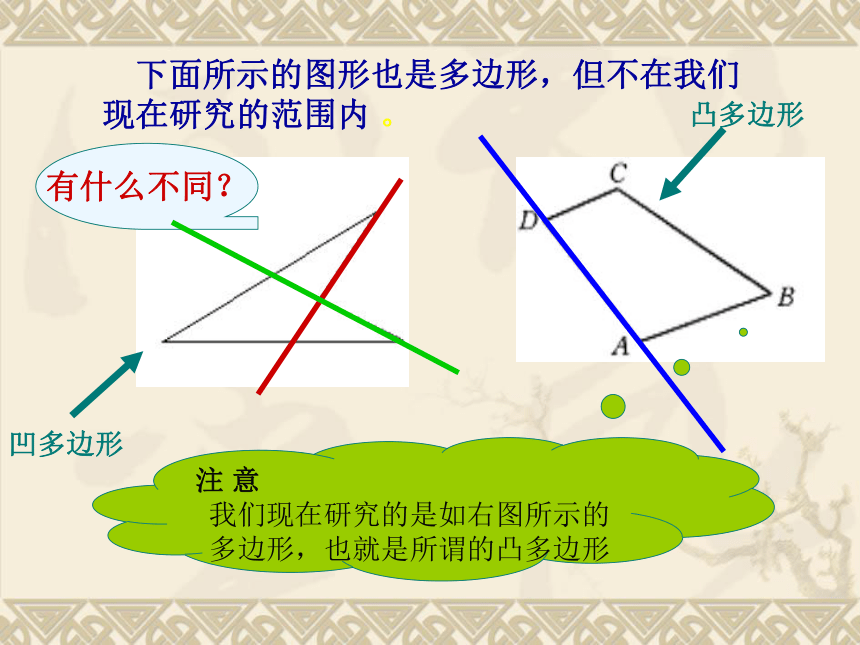
的定义，说出什么叫四边形吗？四边形是由四条不在同一直线上的线段首尾顺次相接组成的平面图形，记为四边形ABCD 什么叫五边形？五边形，它是由五条不在同一直线上的线段首尾顺次连结组成的平面图形，记为五边形ABCDE 一般地，由一些不在同一直线上的线段首尾顺次相接组成的平面图形叫做多边形那么多边形的定义呢？A1A2A3A4A5An 下面所示的图形也是多边形，但不在我们现在研究的范围内 。注 意
我们现在研究的是如右图所示的多边形，也就是所谓的凸多边形 有什么不同？凹多边形凸多边形边顶点外角内角1.如图8.3.2所示，∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角 3.∠CBE和∠ABF都是与∠ABC相邻的外角， 两者互为对顶角，四边形有八个外角。
既然三角形有三个内角、三条边，六个外角，那么四边形有几个内角？几条边？几个外角呢？2.AB，BC，CD，DA是四边形ABCD的四条边
那么五边形有几个内角？几条边？几个外角呢？
那么六边形有几个内角？几条边？几个外角呢？
那么n边形有几个内角？几条边？几个外角呢？
六边形有6个内角，6条边，12个外角
五边形有5个内角，5条边，10个外角
n边形有n个内角，n条边，2n个外角
请大家细心地填一填，多边形的内角，边，外角三者的关系表，你能发现什么规律？3344556677nn681012142n 三角形如果三条边都相等，三个角也都相等，那么这样的三角形就叫做正三角形。 如果多边形各边都相等，内角也都相等，那么这样的多边形就叫做正多边形。如正三角形、正四边形（正方形）、正五边形等等 。正三角形正四边形正五边形正六边形正八边形(或正三边形)(或正方形) 连结多边形不相邻的两个顶点的线段叫做多边形的对角线. 线段AC是四边形ABCD的一条对角线；
多边形的对角线用虚线表示。 我们已经知道一个三角形的内角和等于180°，那么四边形的内角和等于多少呢？五边形、六边形呢？由此，n边形的内角和等于多少呢？
探索新知345n-2540 °720 °900 °180 ° (n-2)1.从一个顶点出发由此，我们就可以得出 :n边形的内角和为_________________．(n-2) ×180 °
它有什么作用呢?1.知道多边形的边数,可以求出多边形的内角和.2.知道多边形的内角和,可以求出多边形的边数.例1.求八边形的内角和的度数． 解 　（n－2）×180°
=（8－2）×180°
=1 080° 分析: n边形的内角和公式为(n-2) 180 ° ,
现在知道这个多边形的边数是，
代入这个公式既可求出.例2.已知多边形的内角和的度数为900°，则这个多边形的边数为________解 　（n－2）×180° = 900°
（n－2）= 900° /180°
（n－2） = 5
n= 5 +2
n=7
7哇!这么简单呀! 例3. 已知在一个十边形中，九个内角的和的度数是1290°，求这个十边形的另一个内角的度数.解: （10－2）×180° =1440 °
则十边形的另一个内角的度数为
1440 °- 1290° =150 °先求出十边形的内角和
再减去1290°,就可以得出.那么对于正多边形来说,又遇到怎样的问题呢?因为正多边形的每个角相等,所以知道
正多边形的边数,就可以求出每一个内角的度数.（n－2）×180°/ n例4.正五边形的每一个内角等于_____,外角等于___.解: （n－2）×180°/ n
= （5－2）×180°/5
=540°/5
=108°
前面我们学习了三角形的外角和是360 ° ，当时是怎样研究出来的？ABCDEF容易看出，3个外角+3个内角=3个平角
而3个内角的和是180 ° ，
那么三角形的外角和就是3X 180°-180°= 360那么你能研究出四边形的外角和吗？整体思路：1.先求4个外角+4个内角的和；
2.再减去4个内角的和容易看出，4个外角+4个内角=4个平角
而4个内角的和是360 ° ，
那么四边形的外角和就是4X 180°-360°= 360°ABCD1234那么出五边形，六边形，n边形的外角和吗？
五边形的外角和就是5X 180°-540°= 360 °
六边形的外角和就是6X 180°-720°= 360°
。。。。。。
n边形的外角和就是nX 180°- (n-2)X 180°
= (n-n+2)X 180° = 360 °任意多边形的外角和都为3
6
0 ° 例5.正五边形的每一个外角等于___.每一个内角等于_____,72°144°例6.如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____6例7.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____A.12 B.9 C. 8 D.7A例8.如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____12 今天你学到了什么知识？你能用自己的话说说吗？下课了!同学们:路漫漫而其修远兮!吾将上下而求索!