展开与折叠

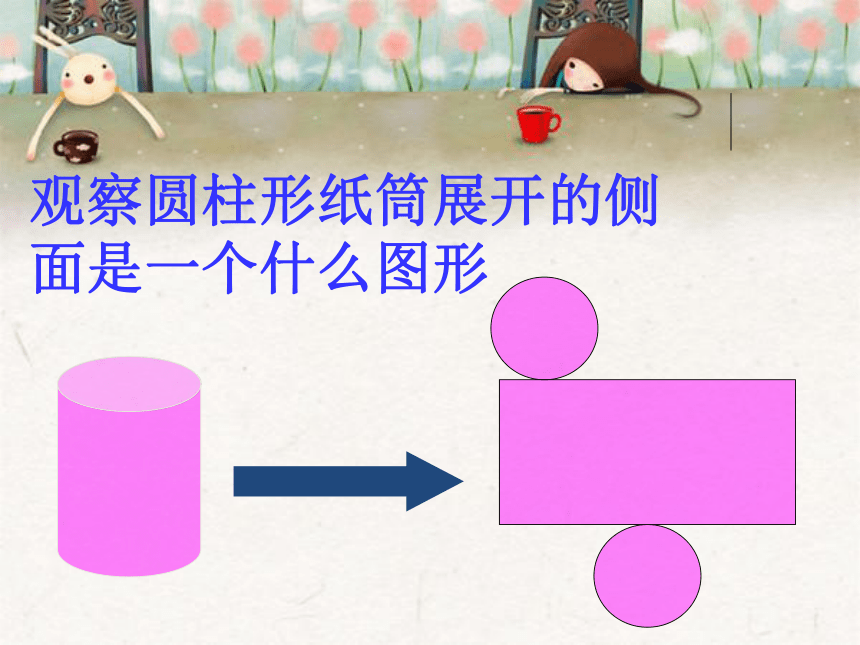
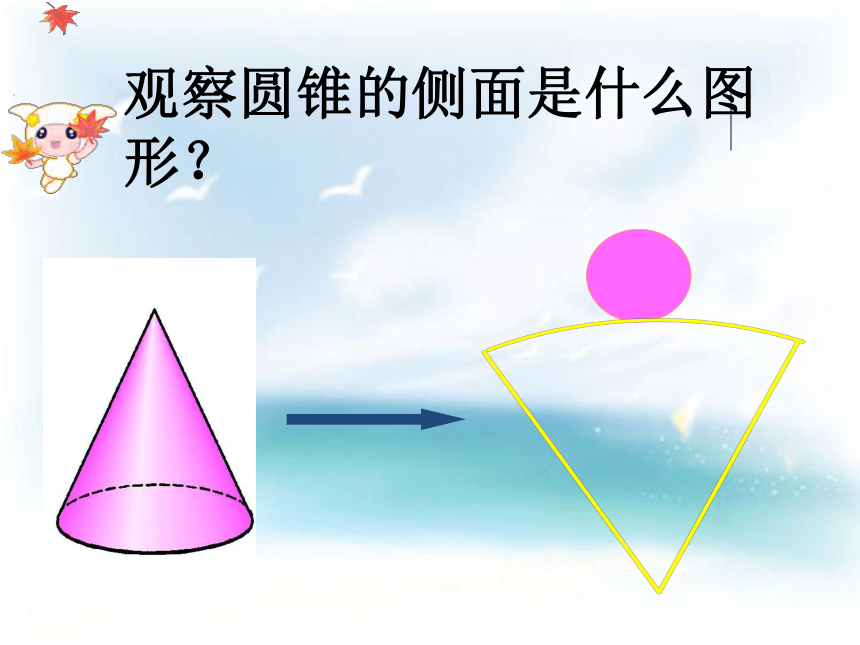
课件27张PPT。展开与折叠观察圆柱形纸筒展开的侧面是一个什么图形 观察圆锥的侧面是什么图形？
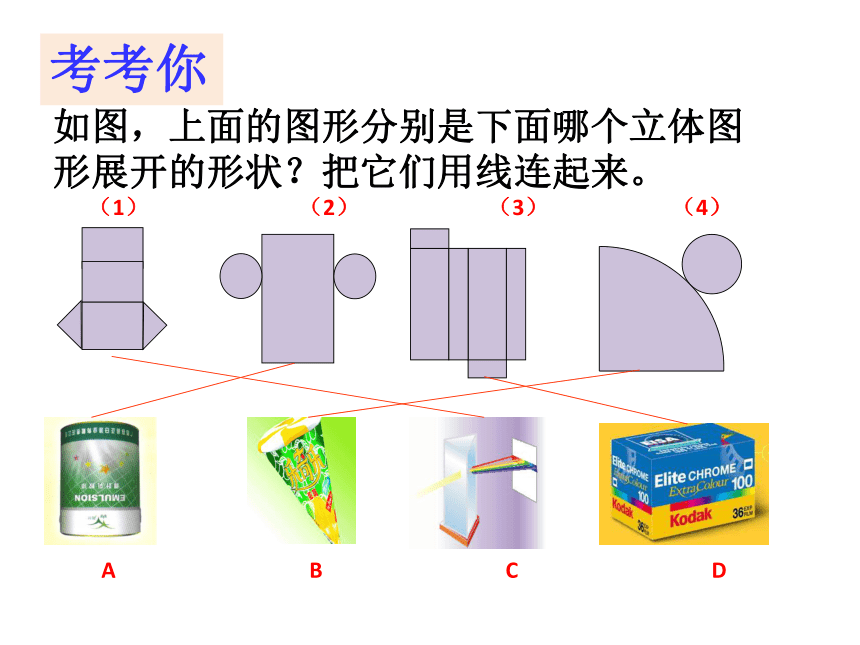
如图，上面的图形分别是下面哪个立体图形展开的形状？把它们用线连起来。考考你 （1） （2） （3） （4） A B C DNo 1 还是能够认出你！
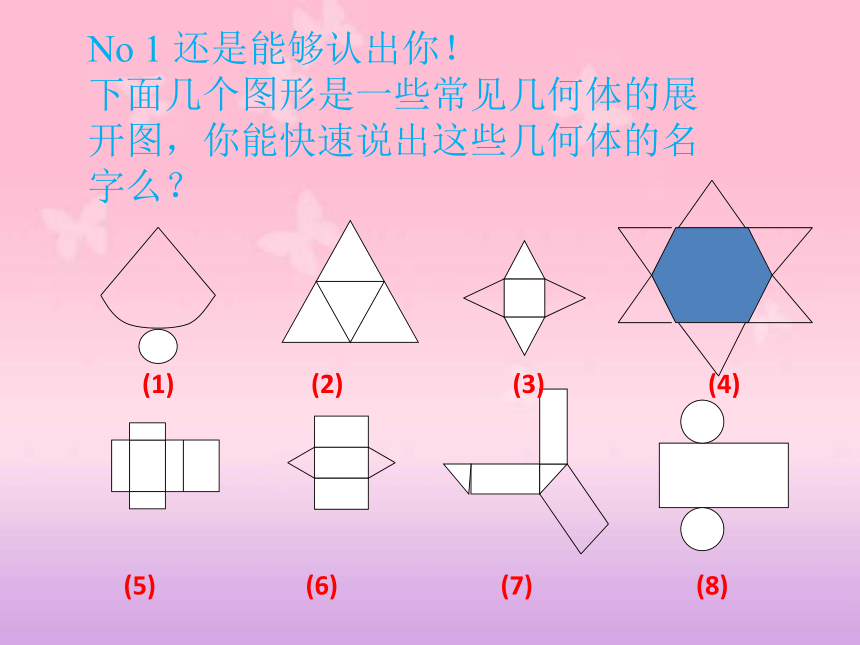
下面几个图形是一些常见几何体的展开图，你能快速说出这些几何体的名字么？ 将一个正方体的表面沿某些棱剪开,你能得到哪些平面图形？与同伴进行交流.回忆城能否将得到的平面图形分类？
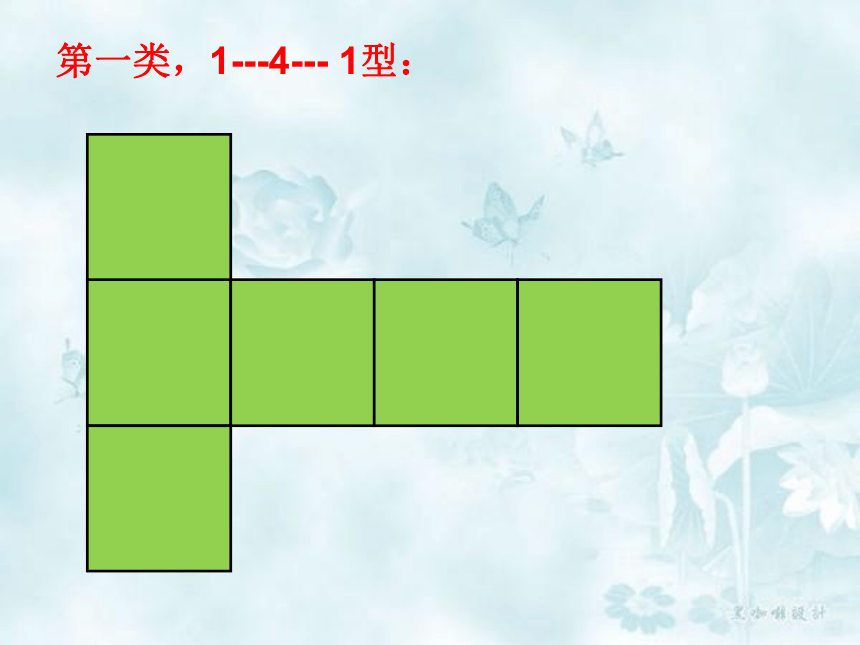
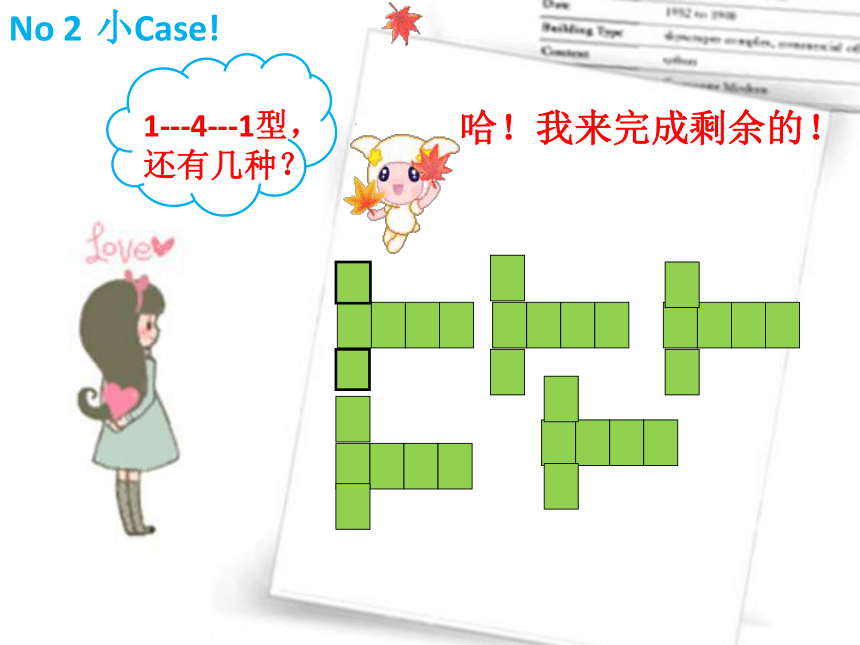
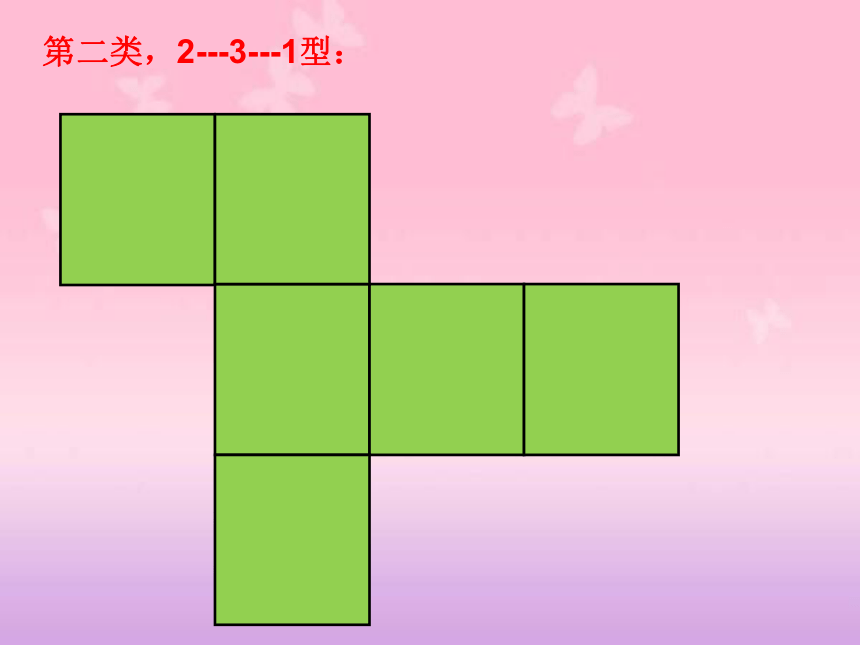
你是按什么规律来分类的？ 第一类，1---4--- 1型：哈！我来完成剩余的！No 2 小Case! 第二类，2---3---1型：共？种。我来画一画！第三类，2---2---2型，只有一种。第四类，3---3型，只有一种。正方体的表面展开图用“口诀”：一线不过四，
田凹应弃之;
相间、“Z”端是对面，
间二、拐角邻面知。总结规律：田凹应弃之相间、“Z”端是对面A和B为相对的两个面间二、拐角邻面知C和D为相邻的两个面我的几何直觉！如图是一个正方体纸盒的展开图，想一想，再试一试面A，面B，面C的对面各是哪个面？ ABCDEFA F B D C ENo 3 小菜一碟！5



B考考你棒KEY:(3)、如果“你”在前面，那么什么在后面？(4)李明为好友制作一个（图1）正方体礼品盒，六面上各有一字，连起来就是“预祝中考成功”，其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是（　　）
CA与B两点沿着侧面的最短路线是什么？ 最短路线问题：BB(2)A与B两点沿着正方体表面的最短路线是什么？你能想出几种获得最短路线的方法呢？ 能力大拓展：若是沿着长方体呢？蚂蚁的智慧：
某同学的茶杯是圆柱形，如图是茶杯的立体图，左边下方有一只蚂蚁，从A处爬行到对面的中点B处，如果蚂蚁爬行路线最短，请画出这条最短路线图．
解：如图，将圆柱的侧面展开成一个长方形，如图示，则A、B分别位于如图所示的位置，连接AB，即是这条最短路线图．
No 4 我来帮帮你！：已知正方若已知两点之间的所有连线中，线段最短，那么你能否试着解决下面的问题呢?正方体的顶点A处有一只蜘蛛，B处有一只小虫，如图所示，请你在图上作出一种由A到B的最短路径，使得这只小蜘蛛能在最短时间内捉住这只小虫子.
看我学会了多少？O(∩_∩)o！我来露一手！