1.2.2集合的运算

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
教 案 纸
课 题 交集与并集 课型
主备课人 上课教师 上课时间
学习目标 学生通过观察、类比、，借助Venn图，理解集合的基本运算
教学重点 交集和并集的含义和运算
教学难点 交集，并集的运算
教师准备 多媒体
反思本节课同学对概念的理解不够 教学环节 教学内容 师生互动 设计意图
复习引入 下面两个问题，你能说出集合C与集合A,B之间的关系吗？A=｛2.4.6.8｝，B=｛3.5.6.7｝，C={6}.A={x|x>1},B={x|x<3},C={x|1概念形成 给出交集定义：一般地，由所有属于A且属于B的元素所组成的集合,叫做A,B的交集．记作AB（读作‘A交B’），即AB=｛x|xA，且xB｝．
概念的深化 (1)AA=A AΦ=Φ，AB=BA (2)ABA, ABB．(2)若AB则AB=A AB=A (3)若A=B, 则AA=A 教师总结出交集有关性质 学生积极投入交流
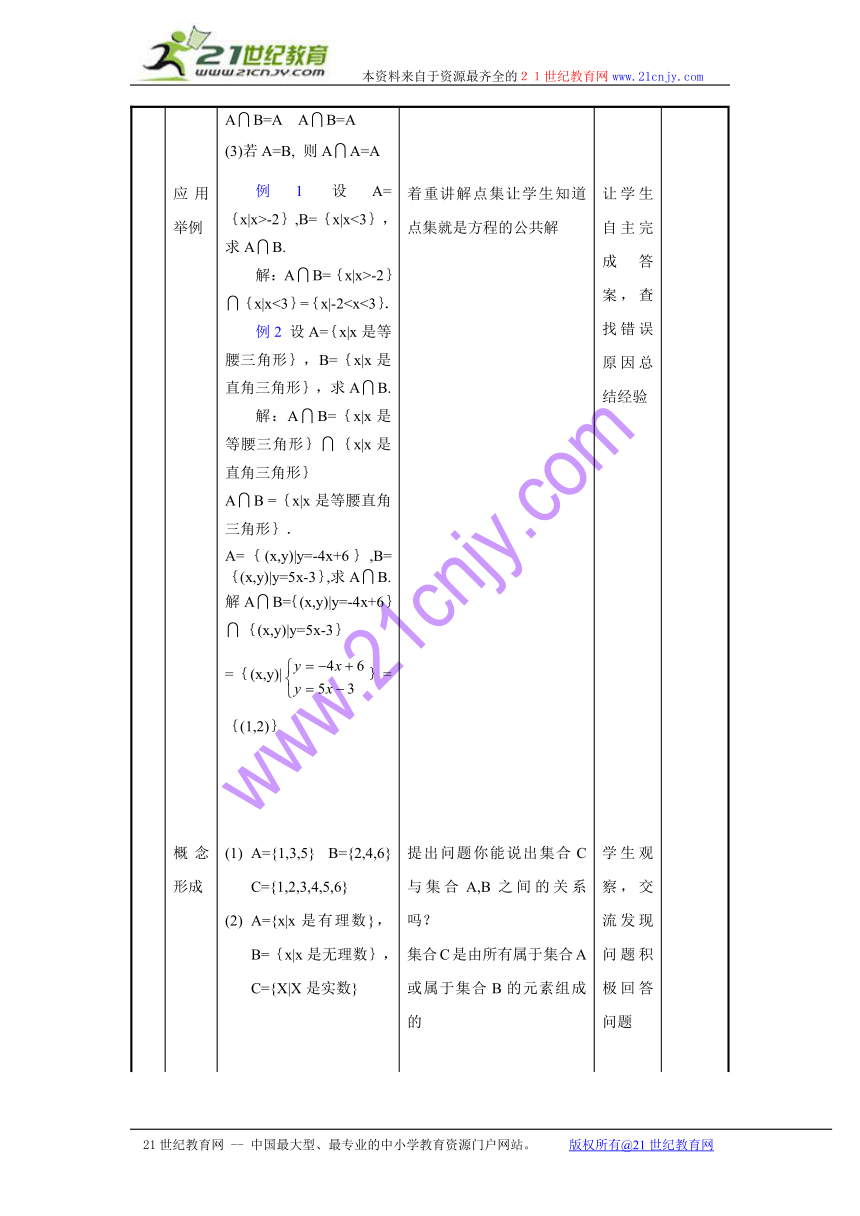
应用举例 例1 设A=｛x|x>-2｝,B=｛x|x<3｝，求AB.解：AB=｛x|x>-2｝｛x|x<3｝=｛x|-2概念形成 A={1,3,5} B={2,4,6} C={1,2,3,4,5,6}A={x|x是有理数}，B=｛x|x是无理数｝，C={X|X是实数} 提出问题你能说出集合C与集合A,B之间的关系吗？集合C是由所有属于集合A或属于集合B的元素组成的 学生观察，交流发现问题积极回答问题
概念深化 一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做A,B的并集．记作：AB（读作‘A并B’），即AB ={x|xA，或xB})．2．并集的性质(1)AA=A (2)AΦ=A (3)AB=BA (4)ABＡ,ABB 有学生归纳老师给予补充你能根据交集的性质总结出并集的有关性质么？ 学生思考总结
应用举例 例3 A=｛4,5,6,8｝,B=｛3,5,7,8｝，求AB.解：AB=｛3,4,5,6,7,8｝．例4设A=｛x|x是锐角三角形｝，B=｛x|x是钝角三角形｝，求AB.解：AB=｛x|x是锐角三角形｝｛x|x是钝角三角形｝=｛x|x是斜三角形｝．例5设A=｛x|-1应课堂练习 例一设集合A={-4，2m-1,m2}，B={9，m-5，1-m}，又AB={9},求实数m的值.解：∵AB={9}，A={-4，2m-1,m2}，B={9，m-5，1-m}，∴2m-1=9或m2=9，解得m=5或m=3或m=-3.若m=5，则A={-4，9，25}，B={9，0，-4}与AB={9}矛盾；若m=3，则B中元素m-5=1-m=-2，与B中元素互异矛盾；若m=-3，则A={-4，-7，9}，B={9，-8，4}满足AB={9}.∴m=-3．例二A={x|x2+ax+b=0},B={x|x2+cx+15=0},又AB={3，5}，A∩B={3}，求实数a,b,c的值.解：∵A∩B={3},∴3∈B，∴32+3c+15=0，∴c=-8.由方程x2-8x+15=0解得x=3或x=5，∴B={3，5}.由A（AB={3，5}知，3∈A，5A（否则5∈A∩B，与A∩B={3}矛盾）故必有A={3}，∴方程x2+ax+b=0有两相同的根3，由韦达定理得3+3=-a，33=b，即a=-6,b=9，c=-8. 教师让个别学生上黑板板书，其他学生在下边做，及时纠错。 主主动思考，加深理解概念
归归纳小结 交集并集的概念利用所学知识解决实际问题 主主动思考，加深理解概念
做作业 教材联系B 2.3.4题
板书一 交集的概念与性质 二 例题讲解 例一 1）（2） （ 三并集的概念与性质例五 四 练习五 小结
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网