1.21集合的表示法
图片预览






文档简介
课件20张PPT。集合之间的关系自学书P10-P13回答下列问题
1.集合之间有那些关系
2.子集,真子集,集合相等的定义
3.子集,真子集的性质
4.集合关系与其特征性质之间的关系自学提纲引:观察下列集合S ={x |x > 3},T ={x |3x – 6 > 0}
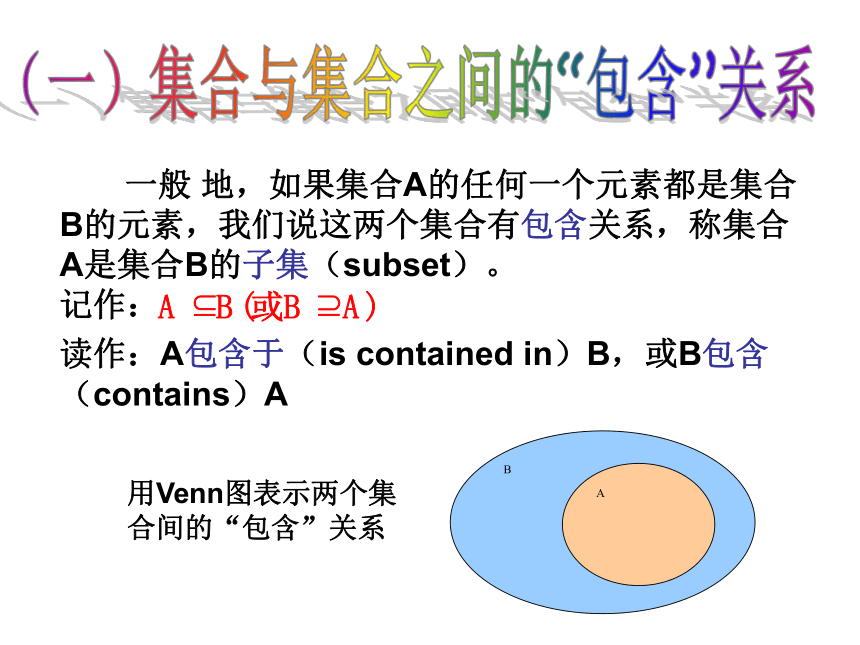
E ={x |(x + 1)(x - 2)=0},F ={-1,-2}(一)集合与集合之间的“包含”关系 一般 地,如果集合A的任何一个元素都是集合B的元素,我们说这两个集合有包含关系,称集合A是集合B的子集(subset)。
记作:
读作:A包含于(is contained in)B,或B包含(contains)A用Venn图表示两个集合间的“包含”关系 写出{1,2,3}的所有子集(二)集合与集合之间的“相等”关系定义:如果集合A的任何一个元素都是集合B的元素,同时集合B任何一个元素都是集合A的元素,我们就说集合A等于集合B,记作A=B一个集合有多种表达形式.(1)A ={1,3},B = {1,3,5,6}
(2)C = {x | x是矩形}
D ={x | x是平行四边形}
(3)P ={x |x是菱形},Q ={x |x是正方形}
(4)S ={x |x > 3},T ={x |3x – 6 > 0}
(三)真子集的概念定义:如果集合A是集合B的子集,并且集合B至少有一个元素不属于A,那么集合A叫做集合B的真子集,记作A B读作:A真包含于B,或B真包含A用Venn图表示两个集合间的“真包含”关系写出{1,2,3,}的
(1)所有真子集?
(2)非空子集?
(3)非空真子集?
(四)子集与真子集的性质 (五)集合的关系与其特征性质之间的关系 (六) 与 的区别 1,2,5,7课堂练习书13页练习A,B课堂小结
1.集合之间有那些关系
2.子集,真子集,集合相等的定义
3.子集,真子集的性质
4.集合关系与其特征性质之间的关系自学提纲引:观察下列集合S ={x |x > 3},T ={x |3x – 6 > 0}
E ={x |(x + 1)(x - 2)=0},F ={-1,-2}(一)集合与集合之间的“包含”关系 一般 地,如果集合A的任何一个元素都是集合B的元素,我们说这两个集合有包含关系,称集合A是集合B的子集(subset)。
记作:
读作:A包含于(is contained in)B,或B包含(contains)A用Venn图表示两个集合间的“包含”关系 写出{1,2,3}的所有子集(二)集合与集合之间的“相等”关系定义:如果集合A的任何一个元素都是集合B的元素,同时集合B任何一个元素都是集合A的元素,我们就说集合A等于集合B,记作A=B一个集合有多种表达形式.(1)A ={1,3},B = {1,3,5,6}
(2)C = {x | x是矩形}
D ={x | x是平行四边形}
(3)P ={x |x是菱形},Q ={x |x是正方形}
(4)S ={x |x > 3},T ={x |3x – 6 > 0}
(三)真子集的概念定义:如果集合A是集合B的子集,并且集合B至少有一个元素不属于A,那么集合A叫做集合B的真子集,记作A B读作:A真包含于B,或B真包含A用Venn图表示两个集合间的“真包含”关系写出{1,2,3,}的
(1)所有真子集?
(2)非空子集?
(3)非空真子集?
(四)子集与真子集的性质 (五)集合的关系与其特征性质之间的关系 (六) 与 的区别 1,2,5,7课堂练习书13页练习A,B课堂小结
