1.4.2绝对值

课件18张PPT。1.2.4 绝对值制作者：胡老师1.复习数轴上如何表示一个有理数
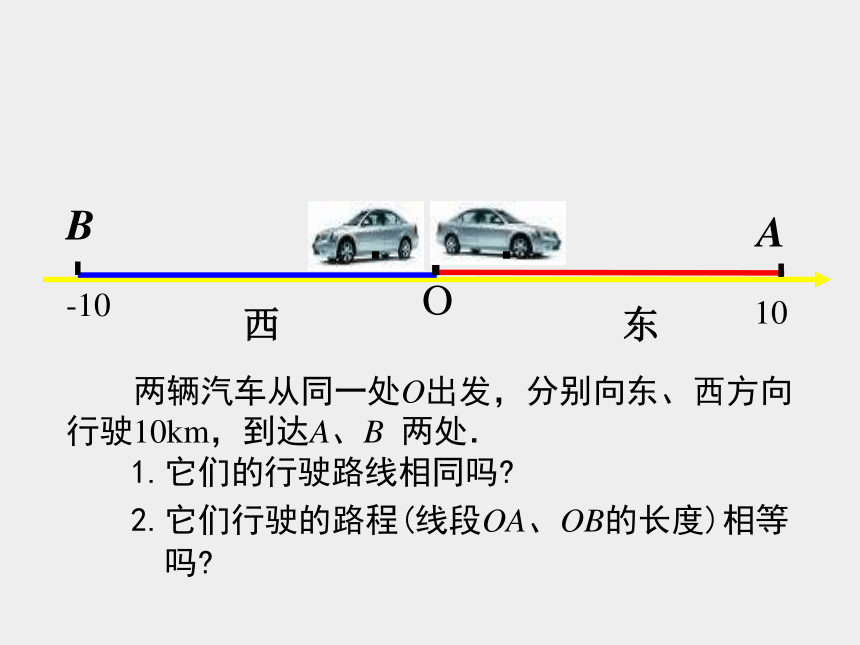
例如，在数轴上表示考虑以下问题：是互为相反数吗？每一对数离原点的距离相等吗？答：是，每一对数离原点的距离相等。这段距离我们应该怎样称呼呢？-10 两辆汽车从同一处O出发，分别向东、西方向行驶10km，到达A、B 两处．2.它们行驶的路程(线段OA、OB的长度)相等
吗?1.它们的行驶路线相同吗?O10BA··东西答：（1）线路不同，一辆向东，一辆向西；
（2）行驶的路程相同的，都是10km. 图中，表示-10的点B和表示10的
点A离开原点的距离都是10，我们把
这个距离10叫做数-10，10的绝对值。绝对值的概念： 一般的，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作 这里，a是任意的有理数。那么，-10的绝对值记作│-10│ ，10的绝对值记作│10│，化简得 ：│-10│=10， │10│ =10那么绝对值为10的数有多少个？ 答：2个，分别是-10和10.+4的绝对值是多少？-5.3的绝对值是多少？答：+4的绝对值是4，-5.3的绝 对值是5.3。或可以这样回答：
│+4│ =4， │-5.3│=5.30的绝对值是多少？0的绝对值是0，即│0│=0 课堂练习：（1）│+2│ = ，│5│= ， │+10.6│= ；
│0│= ；
│-12│ = ， │-20.8│ = ；
2510.601220.8考虑以下问题：
（1）正数的绝对值是什么数？
（2）0的绝对值是什么数？
（3）负数的绝对值是什么数？
小结：一个正数的绝对值是它本身，
一个负数的绝对值是它的相反数，0的绝对值是0.若a是任意的有理数，
当a是正数时， │ a │= ；
当a是负数时， │ a │= ；
当a=0时， │ a │= 。a-a0则有
│ a │≥0任何一个有理数都有绝对值？一个数的绝对值有几个？
有没有一个数的绝对值等于-2？任何一个数的绝对值一定是怎样的数？
绝对值等于2的数有几个？它们是什么？考虑以下问题：答：1.任何的数都有绝对值，一个数的绝对值只有 唯一的一个；
2.没有，任何数的绝对值一定不是负数；
3.绝对值等于2的数有两个，是-2和2。练习课本P12 练习 1，2答案
1.解： │6│=6 ，│-8│=8，│-3.9│=3.9，│100│=100， │0│ =0补充练习：绝对值小于4的整数有 ；
绝对值大于1而小于4的整数有 ；
如果一个数的绝对值是13，那么这个数是 ；
如果 ︱ a︱=4,那么a= .
-3，-2，-1，0，1，2，32，3-13，13±4课堂小结：一个数的绝对值，就是在数轴上表示这个数的点与原点的距离（几何意义）；
正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0；
对任意的有理数a, ︱ a︱≥0,即一个数的绝对值为非负数。作业：课本P15 习题1.2
4， 10