圆周角教学课件
图片预览



文档简介
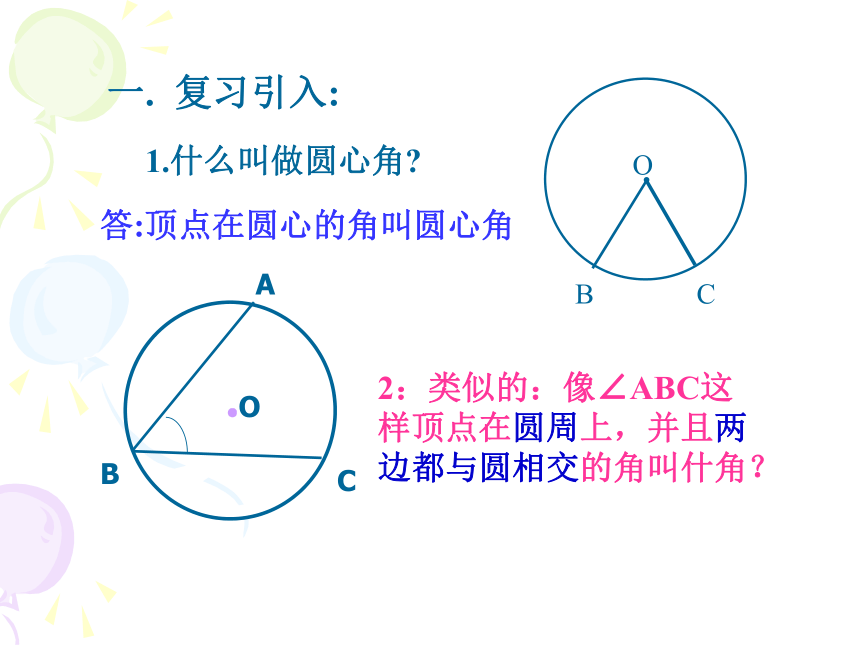
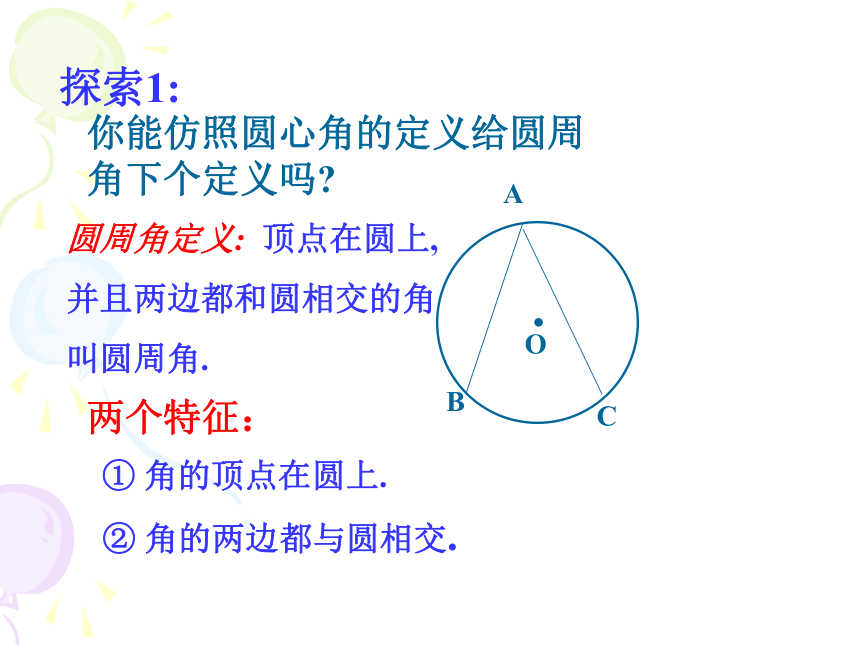
课件21张PPT。24.1.4 圆周角一. 复习引入:1.什么叫做圆心角?OBC答:顶点在圆心的角叫圆心角BAC2:类似的:像∠ABC这样顶点在圆周上,并且两边都与圆相交的角叫什角?探索1:你能仿照圆心角的定义给圆周角下个定义吗?两个特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
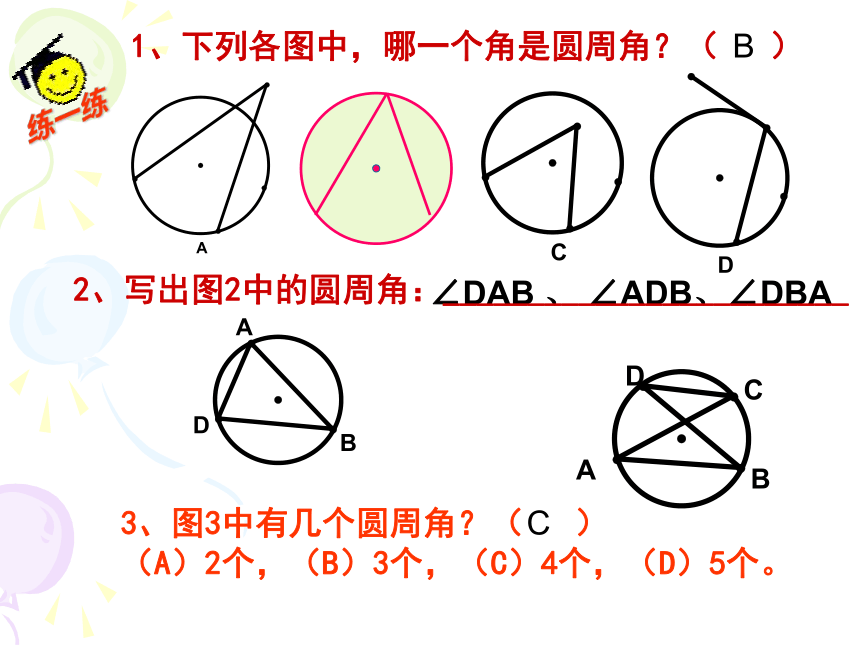
叫圆周角.∠DAB 、 ∠ADB、∠DBA 练一练1、下列各图中,哪一个角是圆周角?( )
3、图3中有几个圆周角?( )
(A)2个,(B)3个,(C)4个,(D)5个。BC2、写出图2中的圆周角:________________________在同一个圆中一条弧所对的圆周角有多少个?
2.这些圆周角的度数是否发生变化?(用量角器量量看)
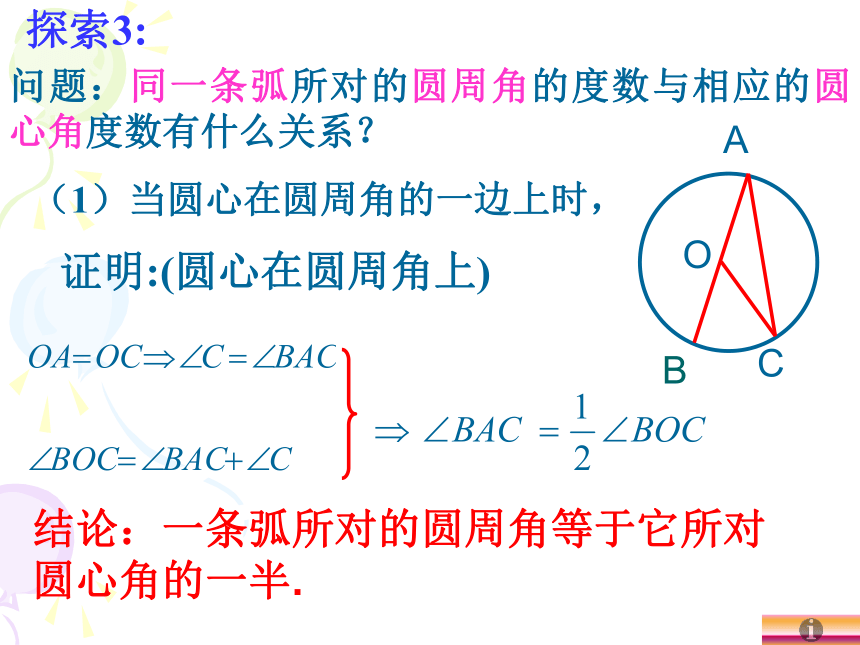
3.同一条弧所对的圆周角与圆心角有什么关系?(用量角器量量看)(画图观察)思考以下问题:探索2:(有无数个)(同一条弧所对的圆周角相等)问题:同一条弧所对的圆周角的度数与相应的圆心角度数有什么关系?
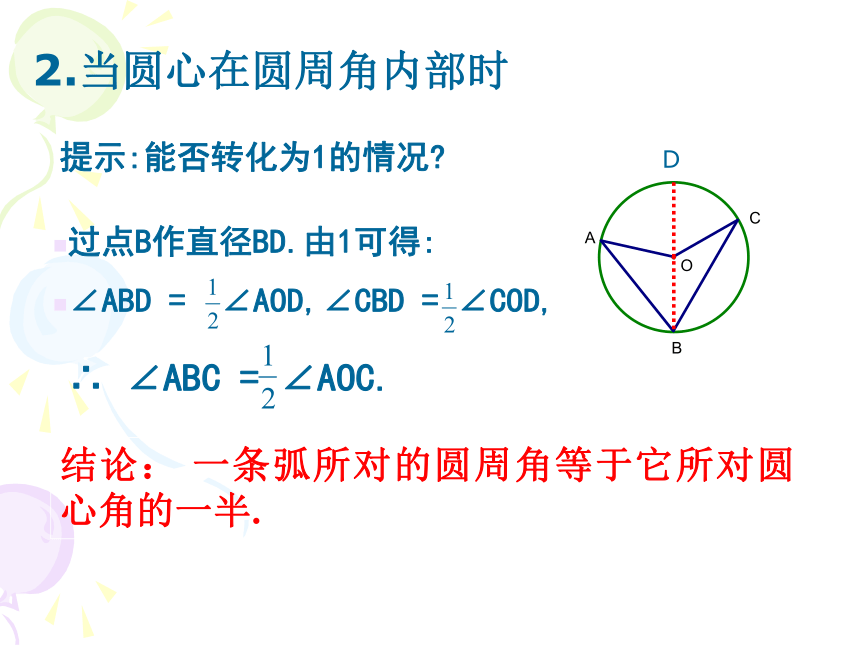
(1)当圆心在圆周角的一边上时,证明:(圆心在圆周角上) 结论:一条弧所对的圆周角等于它所对圆心角的一半.COBA探索3:2.当圆心在圆周角内部时
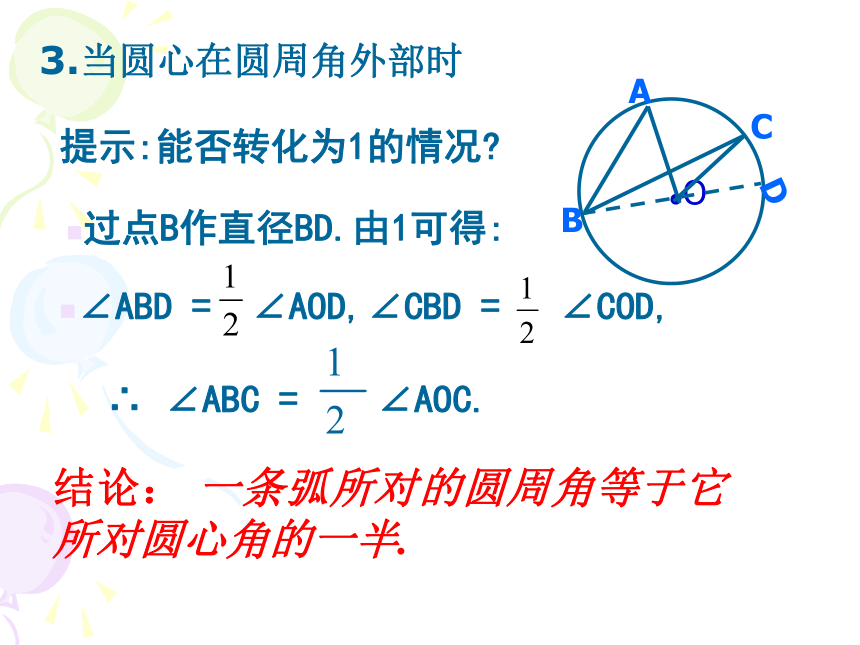
提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,结论: 一条弧所对的圆周角等于它所对圆心角的一半. D3.当圆心在圆周角外部时
结论: 一条弧所对的圆周角等于它所对圆心角的一半. 提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,●ODABC圆周角定理 在同圆或等圆中,同弧或等弧所对的圆周角相等;同一条弧所对的圆周角等于所对的圆心角的一半。 相反,在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧相等吗?在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧也相等 1.半圆或直径所对的圆周角等于多少度?推论:
半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径2.90°的圆周角所对的弦是否是直径?画板3
探索4:·ABC1OC2C3归纳:定理学以致用
1.试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠82、如图,在⊙O中,∠BOC =50°,则∠A的度数为 。.3、已知:△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=60°,则∠AOB的度数为 。
4、已知⊙O中弦AB的等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。25014005.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.6、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°7、如图,BD为⊙O的直径,∠A=30°
BC=4,则BD=_______5008例、如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.又在Rt△ABD中,AD2+BD2=AB2,解:∵AB是直径,∴ ∠ACB= ∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD.例2.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO求证: △ABC 为直角三角形.证明:CO= AB,以AB为直径作⊙O,∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB= ×180°= 90°.∴ △ABC 为直角三角形.圆内接多边形与多边形的外接圆:
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形;
这个圆叫做这个多边形的外接圆.例如:如图,四边形ABCD是⊙O的 ;
⊙O是四边形ABCD的 .探究:圆内接四边形ABCD的对角∠B与∠D有什么关系?结论:圆的内接四边形对角互补。
如图,A、B、C、D是⊙O上的四个点,且∠BCD=100°,求∠BOD( 所对的圆心角)
和∠BAD的大小。变形题:已知ABC三点在圆O上,依次连接ABCO,若∠AOC=140度,求∠B的度数。110度已知圆心角可构造同弧所对的圆周角.D小结:
1、圆周角定理:同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
2、圆周角定理的推论:直径所对的圆周角是直角,900的圆周角所对的弦是直径.
3、圆的内接四边形对角互补。
(在圆中,常作直径,构造直角三角形)想一想:
本节课你有什么收获?
有什么困惑?作业:课本87页4、12
并且两边都和圆相交的角
叫圆周角.∠DAB 、 ∠ADB、∠DBA 练一练1、下列各图中,哪一个角是圆周角?( )
3、图3中有几个圆周角?( )
(A)2个,(B)3个,(C)4个,(D)5个。BC2、写出图2中的圆周角:________________________在同一个圆中一条弧所对的圆周角有多少个?
2.这些圆周角的度数是否发生变化?(用量角器量量看)
3.同一条弧所对的圆周角与圆心角有什么关系?(用量角器量量看)(画图观察)思考以下问题:探索2:(有无数个)(同一条弧所对的圆周角相等)问题:同一条弧所对的圆周角的度数与相应的圆心角度数有什么关系?
(1)当圆心在圆周角的一边上时,证明:(圆心在圆周角上) 结论:一条弧所对的圆周角等于它所对圆心角的一半.COBA探索3:2.当圆心在圆周角内部时
提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,结论: 一条弧所对的圆周角等于它所对圆心角的一半. D3.当圆心在圆周角外部时
结论: 一条弧所对的圆周角等于它所对圆心角的一半. 提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,●ODABC圆周角定理 在同圆或等圆中,同弧或等弧所对的圆周角相等;同一条弧所对的圆周角等于所对的圆心角的一半。 相反,在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧相等吗?在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧也相等 1.半圆或直径所对的圆周角等于多少度?推论:
半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径2.90°的圆周角所对的弦是否是直径?画板3
探索4:·ABC1OC2C3归纳:定理学以致用
1.试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠82、如图,在⊙O中,∠BOC =50°,则∠A的度数为 。.3、已知:△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=60°,则∠AOB的度数为 。
4、已知⊙O中弦AB的等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。25014005.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.6、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°7、如图,BD为⊙O的直径,∠A=30°
BC=4,则BD=_______5008例、如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.又在Rt△ABD中,AD2+BD2=AB2,解:∵AB是直径,∴ ∠ACB= ∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD.例2.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO求证: △ABC 为直角三角形.证明:CO= AB,以AB为直径作⊙O,∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB= ×180°= 90°.∴ △ABC 为直角三角形.圆内接多边形与多边形的外接圆:
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形;
这个圆叫做这个多边形的外接圆.例如:如图,四边形ABCD是⊙O的 ;
⊙O是四边形ABCD的 .探究:圆内接四边形ABCD的对角∠B与∠D有什么关系?结论:圆的内接四边形对角互补。
如图,A、B、C、D是⊙O上的四个点,且∠BCD=100°,求∠BOD( 所对的圆心角)
和∠BAD的大小。变形题:已知ABC三点在圆O上,依次连接ABCO,若∠AOC=140度,求∠B的度数。110度已知圆心角可构造同弧所对的圆周角.D小结:
1、圆周角定理:同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
2、圆周角定理的推论:直径所对的圆周角是直角,900的圆周角所对的弦是直径.
3、圆的内接四边形对角互补。
(在圆中,常作直径,构造直角三角形)想一想:
本节课你有什么收获?
有什么困惑?作业:课本87页4、12
同课章节目录
