高一数学练习:第一章1.1.3集合的基本运算(第2课时补集及综合应用)
文档属性
| 名称 | 高一数学练习:第一章1.1.3集合的基本运算(第2课时补集及综合应用) |
|
|
| 格式 | rar | ||
| 文件大小 | 80.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-20 00:00:00 | ||
图片预览

文档简介
1.设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合?U(A∩B)中的元素共有( )
A.3个 B.4个
C.5个 D.6个
【解析】 A∩B={4,7,9},A∪B={3,4,5,7,8,9},?U(A∩B)={3,5,8},故选A.
【答案】 A
2.已知全集U=R,则正确表示集合M={-1,0,1}和
N={x|x2+x=0}关系的韦恩(Venn)图是( )
【解析】 ∵M={-1,0,1},N={0,-1},
∴N?M,故选B.
【答案】 B
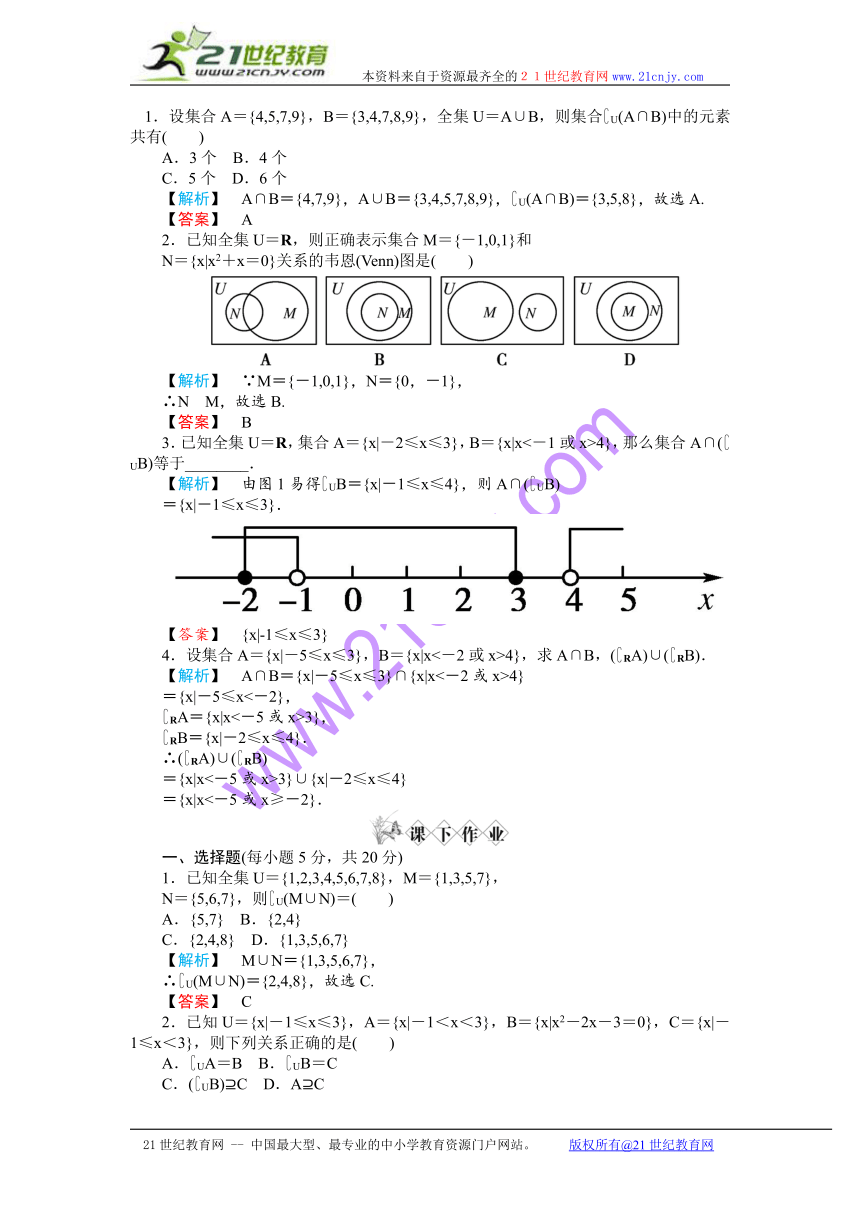
3.已知全集U=R,集合A={x|-2≤x≤3},B={x|x<-1或x>4},那么集合A∩(?UB)等于________.
【解析】 由图1易得?UB={x|-1≤x≤4},则A∩(?UB)
={x|-1≤x≤3}.
【答案】 {x|-1≤x≤3}
4.设集合A={x|-5≤x≤3},B={x|x<-2或x>4},求A∩B,(?RA)∪(?RB).
【解析】 A∩B={x|-5≤x≤3}∩{x|x<-2或x>4}
={x|-5≤x<-2},
?RA={x|x<-5或x>3},
?RB={x|-2≤x≤4}.
∴(?RA)∪(?RB)
={x|x<-5或x>3}∪{x|-2≤x≤4}
={x|x<-5或x≥-2}.
一、选择题(每小题5分,共20分)
1.已知全集U={1,2,3,4,5,6,7,8},M={1,3,5,7},
N={5,6,7},则?U(M∪N)=( )
A.{5,7} B.{2,4}
C.{2,4,8} D.{1,3,5,6,7}
【解析】 M∪N={1,3,5,6,7},
∴?U(M∪N)={2,4,8},故选C.
【答案】 C
2.已知U={x|-1≤x≤3},A={x|-1<x<3},B={x|x2-2x-3=0},C={x|-1≤x<3},则下列关系正确的是( )
A.?UA=B B.?UB=C
C.(?UB)?C D.A?C
【解析】 B={-1,3},?UA={-1,3},
∴?UA=B.
【答案】 A
3.
设U=Z,A={1,3,5,7,9},B={1,2,3,4,5},则图中阴影部分表示的集合是( )
A.{1,3,5}
B.{1,2,3,4,5}
C.{7,9}
D.{2,4}
【解析】 由Venn图可知阴影部分表示的集合为B∩(?UA)={2,4}.
【答案】 D
4.已知U=R,A={x|x>0},B={x|x≤-1},则
(A∩?UB)∪(B∩?UA)=( )
A.? B.{x|x≤0}
C.{x|x>-1} D.{x|x>0或x≤-1}
【解析】 ?UB={x|x>-1},?UA={x|x≤0},则A∩?UB
={x|x>0},B∩?UA={x|x≤-1},
∴(A∩?UB)∪(B∩?UA)={x|x>0或x≤-1}.故选D.
【答案】 D
二、填空题(每小题5分,共10分)
5.设全集U=A∪B={x|1≤x<10,x∈N+},若A∩(?UB)
={m|m=2n+1,n=0,1,2,3,4},则集合B=________.
【解析】 ∵x∈N*,∴U=A∪B={1,2,3,…,9}.
又∵A∪B=U,∴?UB=A,
∴A∩(?UB)=?UB={1,3,5,7,9},
∴B={2,4,6,8}.
【答案】 {2,4,6,8}
6.已知A={x|x≤1或x>3},B={x|x>2},则(?RA)∪B=
________.
【解析】 ?RA={x|1<x≤3},
∴(?RA)∪B={x|x>1}.
【答案】 {x|x>1}
三、解答题(每小题10分,共20分)
7.设全集为R,A={x|3≤x<7},B={x|2【解析】 把全集R和集合A、B在数轴上表示如下:
由图知,A∪B={x|2∴?R(A∪B)={x|x≤2或x≥10}.
∵?RA={x|x<3或x≥7},
∴(?RA)∩B={x|28.集合A={x|x≤-2或x≥3},B={x|aA∪B=R,求实数a,b.
【解析】 ∵A∩B=?,A∪B=R.
∴A与B互为补集.
故B=?RA={x|-2又B={x|a9.(10分)已知U=R,A={x|x2+px+12=0},B={x|x2-5x+q=0},若(?UA)∩B={2},(?UB)∩A=4,求A∪B.
【解析】 由(?UA)∩B={2},
∴2∈B且2?A,
由A∩(?UB)={4},∴4∈A且4?B,
分别代入得
∴p=-7,q=6;
∴A={3,4},B={2,3},
∴A∪B={2,3,4}.
A.3个 B.4个
C.5个 D.6个
【解析】 A∩B={4,7,9},A∪B={3,4,5,7,8,9},?U(A∩B)={3,5,8},故选A.
【答案】 A
2.已知全集U=R,则正确表示集合M={-1,0,1}和
N={x|x2+x=0}关系的韦恩(Venn)图是( )
【解析】 ∵M={-1,0,1},N={0,-1},
∴N?M,故选B.
【答案】 B
3.已知全集U=R,集合A={x|-2≤x≤3},B={x|x<-1或x>4},那么集合A∩(?UB)等于________.
【解析】 由图1易得?UB={x|-1≤x≤4},则A∩(?UB)
={x|-1≤x≤3}.
【答案】 {x|-1≤x≤3}
4.设集合A={x|-5≤x≤3},B={x|x<-2或x>4},求A∩B,(?RA)∪(?RB).
【解析】 A∩B={x|-5≤x≤3}∩{x|x<-2或x>4}
={x|-5≤x<-2},
?RA={x|x<-5或x>3},
?RB={x|-2≤x≤4}.
∴(?RA)∪(?RB)
={x|x<-5或x>3}∪{x|-2≤x≤4}
={x|x<-5或x≥-2}.
一、选择题(每小题5分,共20分)
1.已知全集U={1,2,3,4,5,6,7,8},M={1,3,5,7},
N={5,6,7},则?U(M∪N)=( )
A.{5,7} B.{2,4}
C.{2,4,8} D.{1,3,5,6,7}
【解析】 M∪N={1,3,5,6,7},
∴?U(M∪N)={2,4,8},故选C.
【答案】 C
2.已知U={x|-1≤x≤3},A={x|-1<x<3},B={x|x2-2x-3=0},C={x|-1≤x<3},则下列关系正确的是( )
A.?UA=B B.?UB=C
C.(?UB)?C D.A?C
【解析】 B={-1,3},?UA={-1,3},
∴?UA=B.
【答案】 A
3.
设U=Z,A={1,3,5,7,9},B={1,2,3,4,5},则图中阴影部分表示的集合是( )
A.{1,3,5}
B.{1,2,3,4,5}
C.{7,9}
D.{2,4}
【解析】 由Venn图可知阴影部分表示的集合为B∩(?UA)={2,4}.
【答案】 D
4.已知U=R,A={x|x>0},B={x|x≤-1},则
(A∩?UB)∪(B∩?UA)=( )
A.? B.{x|x≤0}
C.{x|x>-1} D.{x|x>0或x≤-1}
【解析】 ?UB={x|x>-1},?UA={x|x≤0},则A∩?UB
={x|x>0},B∩?UA={x|x≤-1},
∴(A∩?UB)∪(B∩?UA)={x|x>0或x≤-1}.故选D.
【答案】 D
二、填空题(每小题5分,共10分)
5.设全集U=A∪B={x|1≤x<10,x∈N+},若A∩(?UB)
={m|m=2n+1,n=0,1,2,3,4},则集合B=________.
【解析】 ∵x∈N*,∴U=A∪B={1,2,3,…,9}.
又∵A∪B=U,∴?UB=A,
∴A∩(?UB)=?UB={1,3,5,7,9},
∴B={2,4,6,8}.
【答案】 {2,4,6,8}
6.已知A={x|x≤1或x>3},B={x|x>2},则(?RA)∪B=
________.
【解析】 ?RA={x|1<x≤3},
∴(?RA)∪B={x|x>1}.
【答案】 {x|x>1}
三、解答题(每小题10分,共20分)
7.设全集为R,A={x|3≤x<7},B={x|2
由图知,A∪B={x|2
∵?RA={x|x<3或x≥7},
∴(?RA)∩B={x|2
【解析】 ∵A∩B=?,A∪B=R.
∴A与B互为补集.
故B=?RA={x|-2
【解析】 由(?UA)∩B={2},
∴2∈B且2?A,
由A∩(?UB)={4},∴4∈A且4?B,
分别代入得
∴p=-7,q=6;
∴A={3,4},B={2,3},
∴A∪B={2,3,4}.
