15.2多边形内角和

课件14张PPT。多 边 形 内 角 和问题2：长方形和正方形的内角和是多少度？
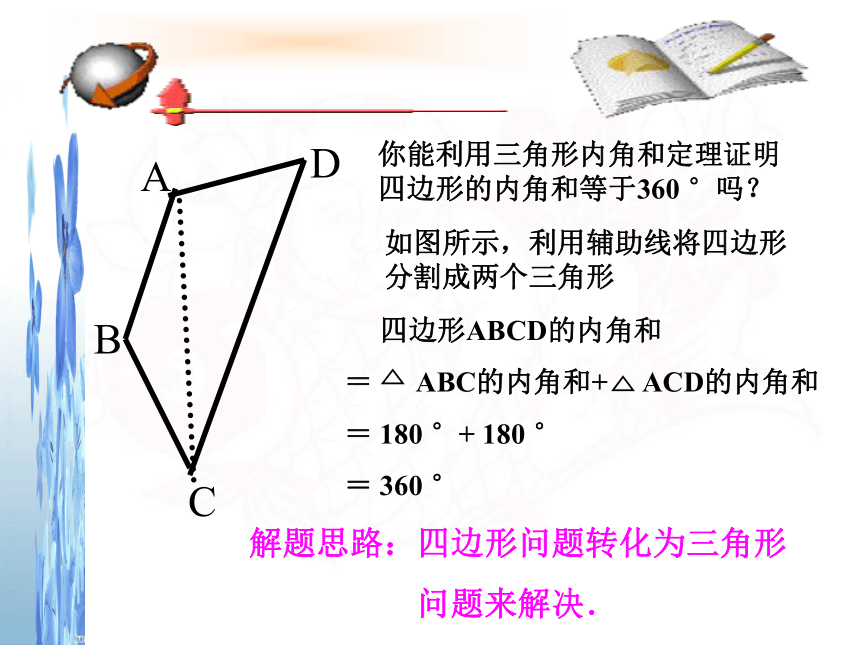
问题1：三角形内角和是多少度？（三角形内角和 180°）（都是360°）导入新知任意一个四边形的内角和是多少度？请同学们任意画一个四边形，用量角器量一下各个内角的度数，计算一下四边形的内角和。猜想：动动手：ABCD如图所示，利用辅助线将四边形分割成两个三角形你能利用三角形内角和定理证明四边形的内角和等于360 °吗？ 四边形ABCD的内角和
＝ ABC的内角和+ ACD的内角和
＝ 180 °+ 180 °
＝ 360 °解题思路：四边形问题转化为三角形
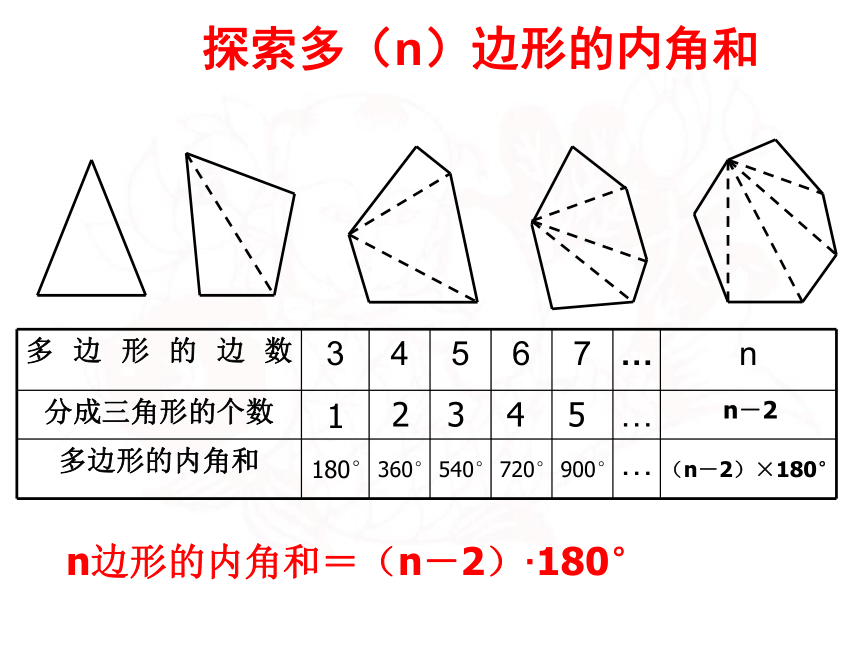
问题来解决．1180° 2345360° 540° 720° 900° n－2 （n－2）×180° n边形的内角和＝（n－2）·180° 探索多（n）边形的内角和 例1 如果一个四边形的一组对角互补，那么另
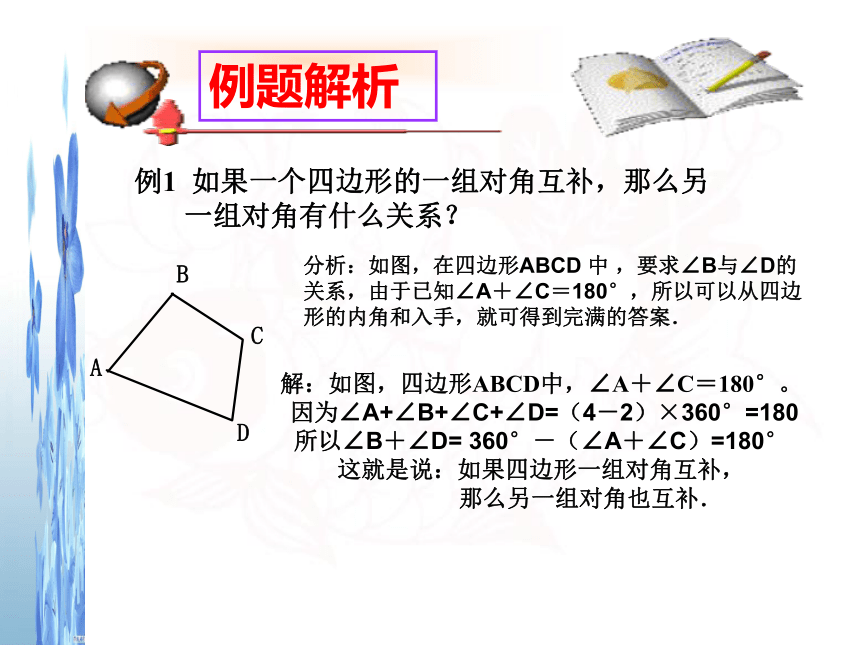
一组对角有什么关系？
解：如图，四边形ABCD中，∠A＋∠C＝180°。
因为∠A+∠B+∠C+∠D=（4－2）×360°=180
所以∠B＋∠D= 360°－（∠A＋∠C）=180°
这就是说：如果四边形一组对角互补，
那么另一组对角也互补．分析：如图，在四边形ABCD 中 ，要求∠B与∠D的关系，由于已知∠A＋∠C＝180°，所以可以从四边形的内角和入手，就可得到完满的答案．例题解析学以致用3、多边形内角和为1080°则它是（ ）边形。 2、十边形的内角和是（ ） ; 如果十边形的各个内角都相等，那么它的一个内角是（ ） 4、多边形内角和为1800°则它是（ ）边形。1、七边形内角和为（ ）900° 1440° 十二 八 144° 多了什么？如何处理？ 这种分割方式，将多边形分成n-1个三角形，故所有三角形的内角和为（n-1）×180 °，边上一点周围所形成的平角不是多边形的内角，因此n边形的内角和为 （n-1）×180 °- 180 °= (n-2)×180 °交流创新 该图中n边形共有n个三角形，故所有三角形内角和为n×180 °，但每个图中都有一个以红圈圈住的点，它是一个圆周角360 °，因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °多了什么？如何处理？交流创新ABDABCDEFCABCDE多了什么？如何处理？ 该图中n边形共有n-1个三角形，故所有三角形内角和为（n-1）×180 °，但每个图中都多了一个三角形的内角和，因此n边形的内角和为 （n-1）×180 °- 180 °= (n-2)×180 °交流创新求下列图形中x的值：课堂练习 如图：某居民小区搞绿化，分别在三角 形、四边形、五边形的广场各角修建半径为1米的花坛。小区绿化组长想先求花坛的面积，再根据面积买花苗。
你能帮绿化组长求出花坛的面积吗？（结果保留π）探究 1、我们学会了许多解决数学问题的思想方法，如将多边形问题转化为三角形问题，以及类比方法，化未知为已知的思想方法等。
2、通过探索多边形的内角和公式，我们尝试了从不同的角度寻求解决问题的方法，并且能有效地解决问题。
3、我们还学会了运用多边形内角和公式进行相关计算。本节课收获必做题：课本P84第1.2.3.4.5
选做题：
如图：我国的国旗上的五星是正五角星，正五角星中的五边形ABCDE是正五边形，你能求出五角星中∠F的度数吗？作业