相似三角形的应用
图片预览





文档简介
课件12张PPT。培风中学 严祖兵相似三角形的应用1︰3相似三角形的判定方法有哪些?
如果两个三角形的相似比为1︰3,那么它们的对应中线之比是 ,对应高之比 ,周长之比 ,面积之比是 。想一想,并回答:1︰31︰31︰91︰3 学了相似三角形后,你知道它可以帮助我们做些什么吗?
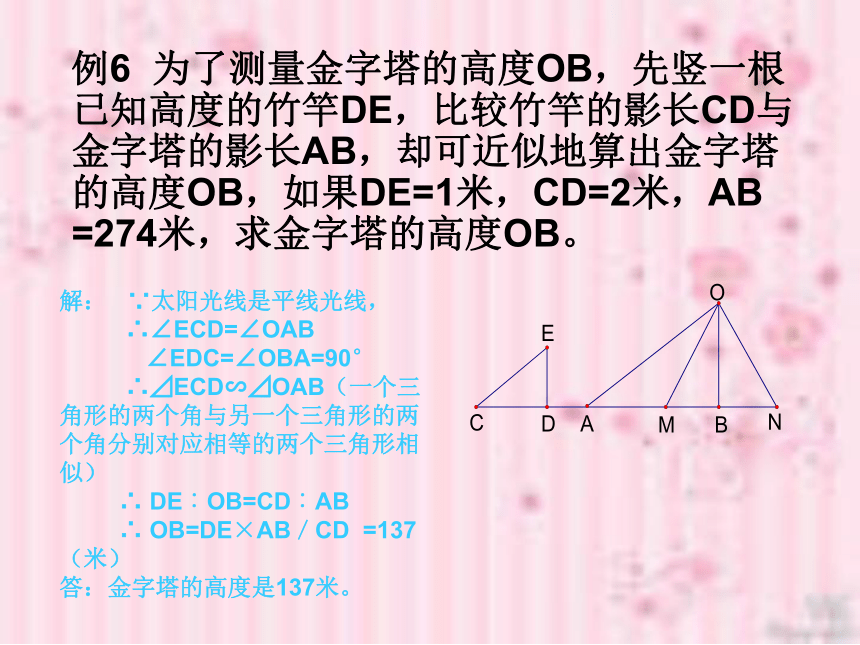
你知道金字塔吗,它们是一些雄伟的建筑,是古代埃及国王的坟墓,2600年前,埃及有一个国王,想知道已盖好的大金字塔的高度,但是他不知道该怎么测量。人爬到塔顶去吧,不可能。因为塔身是斜的,就是爬上去了又怎么测量呢?后来国王请来了一个保叫泰勒斯的学者来帮着他解决了这个问题。你知道他是如何测出来的吧!下面我们就一起来看看他的方法。 古人利用相似三角形性质测建筑物的高度解: ∵太阳光线是平线光线,
∴∠ECD=∠OAB
∠EDC=∠OBA=90°
∴⊿ECD∽⊿OAB(一个三角形的两个角与另一个三角形的两个角分别对应相等的两个三角形相似)
∴ DE︰OB=CD︰AB
∴ OB=DE×AB/CD =137(米)
答:金字塔的高度是137米。 例6 为了测量金字塔的高度OB,先竖一根已知高度的竹竿DE,比较竹竿的影长CD与金字塔的影长AB,却可近似地算出金字塔的高度OB,如果DE=1米,CD=2米,AB =274米,求金字塔的高度OB。
我也行 假如你就是泰勒斯,你会用什么方法来测量呢?请与同桌交流一下。(1)我们可以物理学中的镜面反射来构造相似三角形来解答,如图1:
(2)我们还可以利用三角尺和标杆来测量物体的高度。如图2:图1图2
在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?练一练解:设高楼的高度为x米,则
1.8︰x=3︰60
解之得:x=36
答:高楼的高度为36米。 例7 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和点C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,些时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB。解:∵∠ADB=∠EDC
∴∠ABD=∠ECD=90゜
∴⊿ABD∽⊿ECD(如果一个三角形的两角与另一个
三角形的两角对应相等,那么这两个三角形相似)
∴AB︰CE=BD︰CD
解之得:AB=120ⅹ50/60=100(米)
答:两岸间的大致距离为100米。利用相似三角形测量不可直接测量的宽度利用相似三角形测量瓶子的内径学具准备:等长的两根小木棒,橡皮筋,玻璃瓶,刻度尺过 程:两人合作先把两根小木棒用橡皮筋捆好,然后将等长的两根小木棒的一端放进瓶子里,使两根小木棒抵住瓶底并紧靠瓶子的边缘,再用刻度尺测出小木棒另两端的距离。构造相似并计算瓶子内径。
解:设点O将两根小木棒都分成了1/n,如果我们测出线段AB的长度为m,根据两边对应成比例且夹角相等的两个三角形相似,我们就可以求出内径CD的长度了,即CD=mn。 相似三角形的性质是我们常常用来证明线段等积式的重要方法,也是我们用来求线段的长度与角度相等的重要方法。
例8 如图,已知⊿ACB的边AB、AC上的点,且ADE=∠C,
求证:AD·AB=AE·AC。
解: ∵∠ADE=∠C,∠A=∠A
∴⊿ADE∽⊿ACB(如果一个三角形的两角与另一个三角形的两个角对应相等,那么这两个三角形相似)
∴AD︰AC=AE︰AB
即;AD·AB=AE·AC
通过对本堂课的学习你知道了什么?
你能利用今天所学的知识解决生活与生产中的一些简单的测量问题了吗?课堂小结1、(合作题)测量学校旗杆的高度。
2、习题:第64页第六题作业布置谢谢!
如果两个三角形的相似比为1︰3,那么它们的对应中线之比是 ,对应高之比 ,周长之比 ,面积之比是 。想一想,并回答:1︰31︰31︰91︰3 学了相似三角形后,你知道它可以帮助我们做些什么吗?
你知道金字塔吗,它们是一些雄伟的建筑,是古代埃及国王的坟墓,2600年前,埃及有一个国王,想知道已盖好的大金字塔的高度,但是他不知道该怎么测量。人爬到塔顶去吧,不可能。因为塔身是斜的,就是爬上去了又怎么测量呢?后来国王请来了一个保叫泰勒斯的学者来帮着他解决了这个问题。你知道他是如何测出来的吧!下面我们就一起来看看他的方法。 古人利用相似三角形性质测建筑物的高度解: ∵太阳光线是平线光线,
∴∠ECD=∠OAB
∠EDC=∠OBA=90°
∴⊿ECD∽⊿OAB(一个三角形的两个角与另一个三角形的两个角分别对应相等的两个三角形相似)
∴ DE︰OB=CD︰AB
∴ OB=DE×AB/CD =137(米)
答:金字塔的高度是137米。 例6 为了测量金字塔的高度OB,先竖一根已知高度的竹竿DE,比较竹竿的影长CD与金字塔的影长AB,却可近似地算出金字塔的高度OB,如果DE=1米,CD=2米,AB =274米,求金字塔的高度OB。
我也行 假如你就是泰勒斯,你会用什么方法来测量呢?请与同桌交流一下。(1)我们可以物理学中的镜面反射来构造相似三角形来解答,如图1:
(2)我们还可以利用三角尺和标杆来测量物体的高度。如图2:图1图2
在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?练一练解:设高楼的高度为x米,则
1.8︰x=3︰60
解之得:x=36
答:高楼的高度为36米。 例7 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和点C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,些时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB。解:∵∠ADB=∠EDC
∴∠ABD=∠ECD=90゜
∴⊿ABD∽⊿ECD(如果一个三角形的两角与另一个
三角形的两角对应相等,那么这两个三角形相似)
∴AB︰CE=BD︰CD
解之得:AB=120ⅹ50/60=100(米)
答:两岸间的大致距离为100米。利用相似三角形测量不可直接测量的宽度利用相似三角形测量瓶子的内径学具准备:等长的两根小木棒,橡皮筋,玻璃瓶,刻度尺过 程:两人合作先把两根小木棒用橡皮筋捆好,然后将等长的两根小木棒的一端放进瓶子里,使两根小木棒抵住瓶底并紧靠瓶子的边缘,再用刻度尺测出小木棒另两端的距离。构造相似并计算瓶子内径。
解:设点O将两根小木棒都分成了1/n,如果我们测出线段AB的长度为m,根据两边对应成比例且夹角相等的两个三角形相似,我们就可以求出内径CD的长度了,即CD=mn。 相似三角形的性质是我们常常用来证明线段等积式的重要方法,也是我们用来求线段的长度与角度相等的重要方法。
例8 如图,已知⊿ACB的边AB、AC上的点,且ADE=∠C,
求证:AD·AB=AE·AC。
解: ∵∠ADE=∠C,∠A=∠A
∴⊿ADE∽⊿ACB(如果一个三角形的两角与另一个三角形的两个角对应相等,那么这两个三角形相似)
∴AD︰AC=AE︰AB
即;AD·AB=AE·AC
通过对本堂课的学习你知道了什么?
你能利用今天所学的知识解决生活与生产中的一些简单的测量问题了吗?课堂小结1、(合作题)测量学校旗杆的高度。
2、习题:第64页第六题作业布置谢谢!
