梯形的定义与等腰梯形的性质课件

课件26张PPT。梯形的定义与等腰梯形的性质山东省高密市康成中学 张来志 qq:871414206［课前延伸］［知识链接］
一、复习回顾：
1、同学们，在过去的时间里你们都认识了哪些平面图形啊？请同学们结合对以前图形的认识填写下面括号：

（矩形）（正方形） （圆） （三角形） （平行四边形 ）
2、怎样的图形叫做平行四边形：二、新知引入：
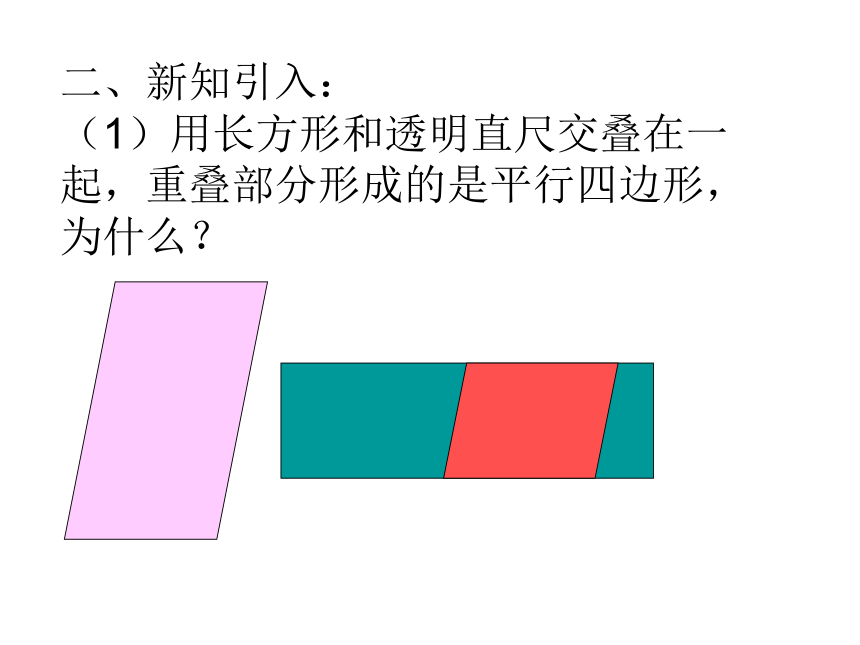
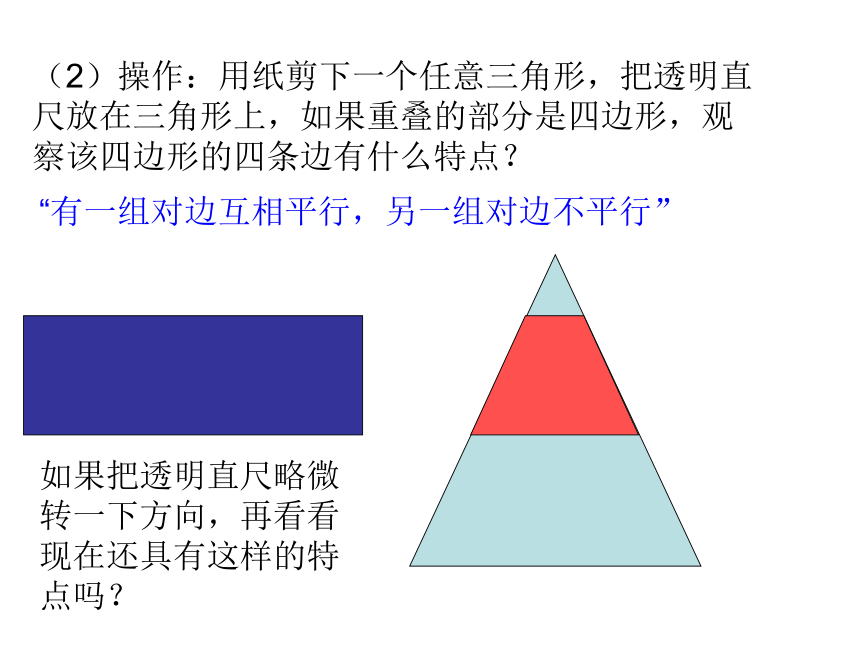
（1）用长方形和透明直尺交叠在一起，重叠部分形成的是平行四边形，为什么？（2）操作：用纸剪下一个任意三角形，把透明直尺放在三角形上，如果重叠的部分是四边形，观察该四边形的四条边有什么特点？
“有一组对边互相平行，另一组对边不平行”如果把透明直尺略微转一下方向，再看看现在还具有这样的特点吗？
（3）你们是怎么知道这一特点的呢？
这个四边形的一组对边是原来长方形的一组对边，所以它们是互相平行的，另一组对边是原来三角形的两条边，它们是不平行的。
（4）你们知道这样的图形叫什么吗:你找到梯形了吗？你找到梯形了吗？
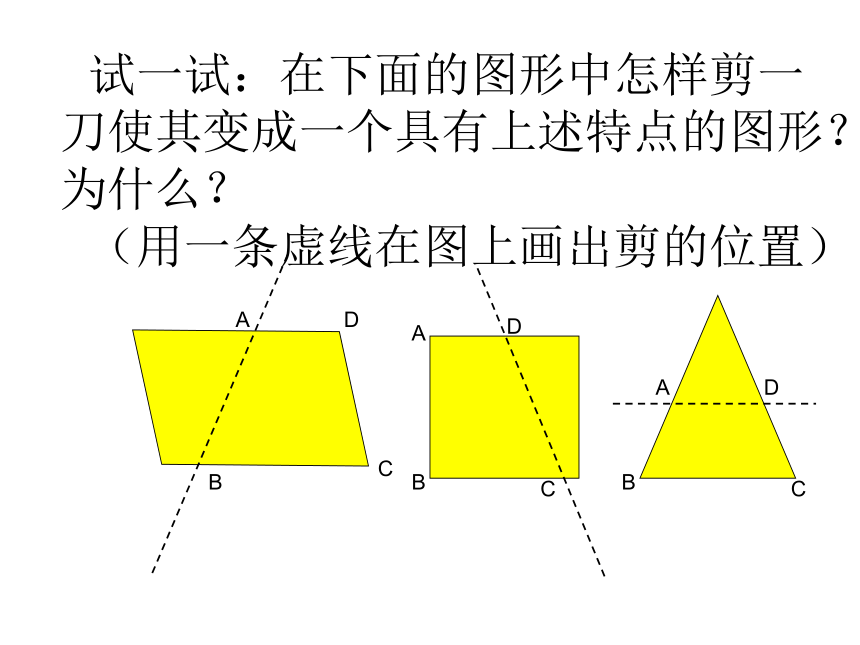
试一试：在下面的图形中怎样剪一刀使其变成一个具有上述特点的图形？为什么？
（用一条虚线在图上画出剪的位置）
ABCDABCDABCD［课内探究］ 一、学习目标：
1、梯形、等腰梯形和直角梯形的有关概念。
2、等腰梯形性质定理的结论及推导过程。
3、等腰梯形性质定理的应用。 A二、自主整理
自学课本27页至29页，完成以下内容：
1、（1）一组对边平行而另一组对边不平行的四边形叫做梯形。
平行的两边叫做梯形的底，
不平行的两边叫做梯形的腰，
在两底之间，与底垂直的线段叫做梯形的高
（2）两腰相等的梯形叫做等腰梯形。
（3）一腰与底垂直的梯形叫做直角梯形。
DCBE有效训练：1、如图，四边形ABCD中，当 ，
且AB不平行于CD时，四边形ABCD是梯形。
2、如图，梯形ABCD中，AD∥BC，
则上底是 ，下底是 ，腰是 。
3、如图，梯形ABCD中，AD∥BC，当 = 时，梯形ABCD是等腰梯形。第1，2，3题图三、新知探究试一试：有一个矩形纸片,如果用剪刀只剪一刀,怎样能得到一个等腰梯形?完成后想一想：1、等腰梯形是轴对称图形吗？如果是，它有几条对称轴？2、等腰梯形同一底上的两个内角的关系呢？ 证明这个结论的正确性：
已知：如图，在梯形ABCD中，AD∥BC ， AB=CD
求证：∠B= ∠C, ∠A= ∠ADC
证明：过点D作DE∥AB，交BC于点E.
于是∠1=∠B
∵AD∥BC，DE∥AB，
∴四边形ABED是平行四边形.
∴AB=DE.
∵AB=CD,
∴DE=CD.
∴∠1=∠C.
∴∠B=∠C.
∵∠A与∠B互补，∠ADC与∠C互补，
∴∠A=∠ADC.ABCDE13、等腰梯形的性质定理1、ABCD谁能想出更好的方法证明性质定理1吗？等腰梯形同一底上的两个内角相等A证法:过点A作AE⊥BC垂足为E
过点D作DF⊥BC垂足为F
由HL定理可得
△ABE≌△DCF
∴∠B=∠C
DBCEF法3：过点C作AB的平行线，
交AD的延长线于点E,则
四边形ABCE为平行四边形
∴AB=CE, ∠B=∠E,∠BCD=∠EDC
又∵AB=CD,
∴CE=CD, ∴∠EDC=∠E
∴∠B=∠BCD
ABDCE证法：延长BA,DC交与点E,由AD∥BC
可得AE=DE, ∴BE=CE, ∴∠B=∠C
BAECD有效训练1、如图，在等腰梯形ABCD中，AD∥BC，AB∥DE ，AD=2，BC=4，则EC= 。
2、如图，在等腰梯形ABCD中，AD∥BC，AB∥DE，AD=2，BC=4， ∠B=60°，则AB= 。 223、上面我们研究了等腰梯形的两组对边的关系及角的关系，那么对于等腰梯形的对角线存在怎样的关系呢？证明这个结论的正确性：
已知：如图，在梯形ABCD中，AD∥BC ,AB=DC
求证：AC=BD
证明： ∵ AD∥BC ,AB=DC ，
∴∠ABC=∠DCB
∴ 在△ABC与△DCB中
∴ AB=CD
∠ABC=∠DCB
BC=CB
∴ △ABC≌△DCB.
∴AC=BD
ADCB平行移对角线等腰梯形的性质定理2:
等腰梯形的两条对角线相等有效训练：
如图：已知在等腰梯形ABCD中， AD ∥ BC，AB=DC，对角线AC⊥ BD，垂足为O，BD =8cm，则梯形ABCD的面积为 。 32cm2三、精讲点拨：例1、如图，在等腰梯形ABCD中,AD∥BC，∠B=60°，AD=15，AB=20，求BC的长。
解: 如图，分别延长BA，CD交于点E。
∵四边形ABCD是等腰梯形，且AD∥BC，
∴∠B=∠C=∠EAD=∠EDA=600.
∴EA=ED，EB=EC.
∴△EAD与△EBC都是等边三角形.
∴BC=BE=BA+AE=BA+AD=20+14=35.
变式训练：
你还更好的添加辅助线的方法，求出BC的长吗？
BCADE课堂小结：这节课的收获是什么？
1、本课学习了梯形、等腰梯形、直角梯形的概念，等腰梯形的性质；
2、通过在等腰梯形中添加适当辅助线，将梯形问题有效地转化为平行四边形及特殊三角形加以解决；等腰梯形中常用的添线方法作 高平行移腰平行移腰平行移对角线延长两腰五、当堂检测
1、梯形ABCD中，AD∥BC，
∠A：∠B=3：1，则∠A= 度。

2、梯形ABCD中，AD∥BC，AB=DC， 若AC=3cm，则BD= cm
3、在梯形ABCD中，AD∥BC，
∠B=90°，∠C=30°，
则∠A= ° ， ∠D= °

4、在等腰梯形ABCD中，AD∥BC，
AB ∥ DE，DF是高，则CF EF。
135 =15090 3 布置作业：
1、完成 课后提升 讲义
2、书本P33 习题A组第2、3题
再见，祝同学们学习进步解：将腰AB平移到DE的位置E∴ 四边形ABED是平行四边形∴ AB∥DE，AB=DE∴ BE=AD=2，AB=DE=CD在等腰△DEC中，DF是高
∴CF= ? EC=1∴ EC=BC – BE = 4 – 2 = 2在Rt △DFC中，
根据勾股定理得CF2+DF2=CD2即 CD2 = 12 + 22 = 5∴ CD=还有其它的方法吗？小结: 四边形的问题我们经常转化为特殊三角形(Rt △)的问题,再利用勾股定理解决.拓展延伸：在等腰梯形ABCD中，AD∥BC，已知AD=2，，BC=4, 高DF=2,求腰CD的长。