2.11变量与函数的概念
图片预览








文档简介
课件22张PPT。1.2.1函数的概念复习提问1.初中所学的函数的概念是什么?
在一个变化过程中有两个变量x和y,
如果对于x的每一个值,y都有唯一的值
与它对应. 那么就说y是x的函数,其中x
叫做自变量.
2.初中学过哪些函数?
正比例函数、反比例函数、一次函数、
二次函数等.
观察探索1.炮弹的射高与时间的变化关系问题; 一枚炮弹发射后,经过26s落到地面击中目标,炮弹的射高为845m,且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化规律为:
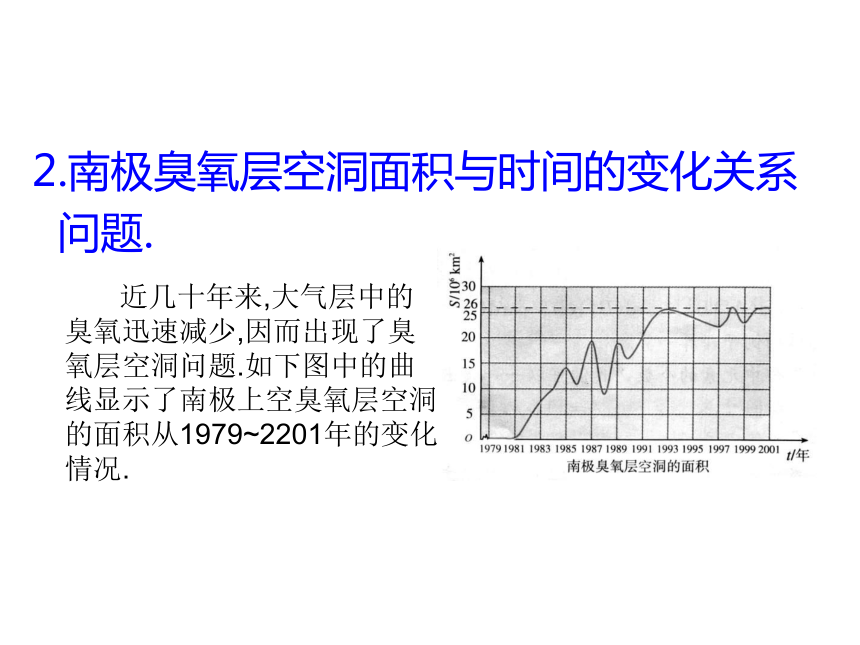
h=130t-5t2 近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.如下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2201年的变化情况.2.南极臭氧层空洞面积与时间的变化关系
问题.恩格尔系数3.“八五”计划以来我国城镇居民的恩格
尔系数与时间的变化关系问题. 国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.如下表 是: “八五”计划以来我国城镇居民的恩格尔系数情况.
(恩格尔系数=食物支出金额/总支出金额)
设A是非空的数集,对于集合A中的任意数x,按照确定的法则f,都有唯一确定的数y与它对应,则这种对应关系叫做集合A上的一个函数1、函数的有关概念:(1)函数的概念:记作:y=f(x),x∈A. 其中,x叫做自变量,x的取值范围A叫做函数的定义域(domain); 与x的值相对应的y值叫做函数值,函数值的集合{f(x)| x∈A }叫做函数的值域(range).注意:②函数符号“y=f(x)”中的f(x)表示与x对应的函数值,一个数,而不是f乘x. 值域① “y=f(x)”是函数符号,可以用任意的字母表示,
如“y=g(x)”;(2)构成函数的三要素是什么?定义域对应关系(3)初中学过哪些函数?它们的定义域、值域、对应法则分别是什么? 比较描述性定义和集合,与对应语言刻画的义,谈谈体会 y=ax2+bx+c (a≠0) y=ax+b (a≠0) y=k/x (k≠0)区间的概念⒈满足不等式a≤x≤b的实数x的集合叫做闭区间,
表示为[a,b]设a,b是两个实数,而且a表示为(a,b)⒊满足不等式a≤x半开半闭区间,表示为[a,b)或(a,b]这里的实数a,b叫做相应区间的端点实数集R可以表示为(-∞,+ ∞)例1:已知函数
(1) 求函数的定义域;
(2)求f(-3),f (2/3)的值;
(3)当a>0时,求f(a),f(a-1)的值. 例2、设一个矩形周长为80,其中一边长为x,
求它的面积关于x的函数的解析式,并写出定义域.几类函数的定义域:(1)如果f(x)是整式,那么函数的定义域是实数集R .(2)如果f(x)是分式,那么函数的定义域是使分母
不等于零的实数的集合 .(3)如果f(x)是二次根式,那么函数的定义域是 使根号内的 式子大于或等于零的实数的集合. (4)如果f(x)是由几个部分的数学式子构成的,
那么函数定义域是使各部分式子都有意义
的实数集合.(即求各集合的交集)(5)满足实际问题有意义.如何判断两个函数是否为同一函数?1. 两个函数的定义域和对应关系完全一致,即称这两个函数相等(或为同一函数)
2. 两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关。例3、下列函数中哪个与函数y=x相等?
(1)y=
(2) y=
(3) y=
(4) y=练习一
判断下列函数f(x)与g(x)是否表示同一个函数,
说明理由?
① f ( x ) = (x -1) 2 ; g ( x ) = 1
② f ( x ) = x ; g ( x ) =
③ f ( x ) = x 2 ;f ( x ) = (x + 1)2
④ f ( x ) = | x | ;g ( x ) = 例1.已知,求解:分析:这是含有未知函数f(x)的等式,比较抽象。由函数
f(x)的定义可知,在函数的定义域和对应法则f不变的条件
下,自变量变换字母,以至变换为其他字母的代数式,对
函数本身并无影响,这类问题正是利用这一性质求解的。方法一:配凑法例1.已知,求解:分析:这是含有未知函数f(x)的等式,比较抽象。由函数
f(x)的定义可知,在函数的定义域和对应法则f不变的条件
下,自变量变换字母,以至变换为其他字母的代数式,对
函数本身并无影响,这类问题正是利用这一性质求解的。方法一:配凑法例1.已知,求解:分析:这是含有未知函数f(x)的等式,比较抽象。由函数
f(x)的定义可知,在函数的定义域和对应法则f不变的条件
下,自变量变换字母,以至变换为其他字母的代数式,对
函数本身并无影响,这类问题正是利用这一性质求解的。方法一:配凑法方法二:令换元法注意点:注意换元的等价性,即要求出 t 的取值范围例2.已知函数f(x)是一次函数,且经过 (1,2),(2,5)求函数y=f(x)的解析式分析:与上一题不同的是这一题已知函数是什么类型的函数,那么我们只需设出相应的解析式模型,通过方程组解出系数即可——待定系数法例3.设f(x)满足关系式 求函数的解析式 分析:如果将题目所给的 看成两个变量,那么该等式即可看作二元方程,那么必定还需再找一个关于它们的方程,那么交换 x与1/x形成新的方程
在一个变化过程中有两个变量x和y,
如果对于x的每一个值,y都有唯一的值
与它对应. 那么就说y是x的函数,其中x
叫做自变量.
2.初中学过哪些函数?
正比例函数、反比例函数、一次函数、
二次函数等.
观察探索1.炮弹的射高与时间的变化关系问题; 一枚炮弹发射后,经过26s落到地面击中目标,炮弹的射高为845m,且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化规律为:
h=130t-5t2 近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.如下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2201年的变化情况.2.南极臭氧层空洞面积与时间的变化关系
问题.恩格尔系数3.“八五”计划以来我国城镇居民的恩格
尔系数与时间的变化关系问题. 国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.如下表 是: “八五”计划以来我国城镇居民的恩格尔系数情况.
(恩格尔系数=食物支出金额/总支出金额)
设A是非空的数集,对于集合A中的任意数x,按照确定的法则f,都有唯一确定的数y与它对应,则这种对应关系叫做集合A上的一个函数1、函数的有关概念:(1)函数的概念:记作:y=f(x),x∈A. 其中,x叫做自变量,x的取值范围A叫做函数的定义域(domain); 与x的值相对应的y值叫做函数值,函数值的集合{f(x)| x∈A }叫做函数的值域(range).注意:②函数符号“y=f(x)”中的f(x)表示与x对应的函数值,一个数,而不是f乘x. 值域① “y=f(x)”是函数符号,可以用任意的字母表示,
如“y=g(x)”;(2)构成函数的三要素是什么?定义域对应关系(3)初中学过哪些函数?它们的定义域、值域、对应法则分别是什么? 比较描述性定义和集合,与对应语言刻画的义,谈谈体会 y=ax2+bx+c (a≠0) y=ax+b (a≠0) y=k/x (k≠0)区间的概念⒈满足不等式a≤x≤b的实数x的集合叫做闭区间,
表示为[a,b]设a,b是两个实数,而且a
(1) 求函数的定义域;
(2)求f(-3),f (2/3)的值;
(3)当a>0时,求f(a),f(a-1)的值. 例2、设一个矩形周长为80,其中一边长为x,
求它的面积关于x的函数的解析式,并写出定义域.几类函数的定义域:(1)如果f(x)是整式,那么函数的定义域是实数集R .(2)如果f(x)是分式,那么函数的定义域是使分母
不等于零的实数的集合 .(3)如果f(x)是二次根式,那么函数的定义域是 使根号内的 式子大于或等于零的实数的集合. (4)如果f(x)是由几个部分的数学式子构成的,
那么函数定义域是使各部分式子都有意义
的实数集合.(即求各集合的交集)(5)满足实际问题有意义.如何判断两个函数是否为同一函数?1. 两个函数的定义域和对应关系完全一致,即称这两个函数相等(或为同一函数)
2. 两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关。例3、下列函数中哪个与函数y=x相等?
(1)y=
(2) y=
(3) y=
(4) y=练习一
判断下列函数f(x)与g(x)是否表示同一个函数,
说明理由?
① f ( x ) = (x -1) 2 ; g ( x ) = 1
② f ( x ) = x ; g ( x ) =
③ f ( x ) = x 2 ;f ( x ) = (x + 1)2
④ f ( x ) = | x | ;g ( x ) = 例1.已知,求解:分析:这是含有未知函数f(x)的等式,比较抽象。由函数
f(x)的定义可知,在函数的定义域和对应法则f不变的条件
下,自变量变换字母,以至变换为其他字母的代数式,对
函数本身并无影响,这类问题正是利用这一性质求解的。方法一:配凑法例1.已知,求解:分析:这是含有未知函数f(x)的等式,比较抽象。由函数
f(x)的定义可知,在函数的定义域和对应法则f不变的条件
下,自变量变换字母,以至变换为其他字母的代数式,对
函数本身并无影响,这类问题正是利用这一性质求解的。方法一:配凑法例1.已知,求解:分析:这是含有未知函数f(x)的等式,比较抽象。由函数
f(x)的定义可知,在函数的定义域和对应法则f不变的条件
下,自变量变换字母,以至变换为其他字母的代数式,对
函数本身并无影响,这类问题正是利用这一性质求解的。方法一:配凑法方法二:令换元法注意点:注意换元的等价性,即要求出 t 的取值范围例2.已知函数f(x)是一次函数,且经过 (1,2),(2,5)求函数y=f(x)的解析式分析:与上一题不同的是这一题已知函数是什么类型的函数,那么我们只需设出相应的解析式模型,通过方程组解出系数即可——待定系数法例3.设f(x)满足关系式 求函数的解析式 分析:如果将题目所给的 看成两个变量,那么该等式即可看作二元方程,那么必定还需再找一个关于它们的方程,那么交换 x与1/x形成新的方程
