2.4.1《函数的零点》
图片预览



文档简介
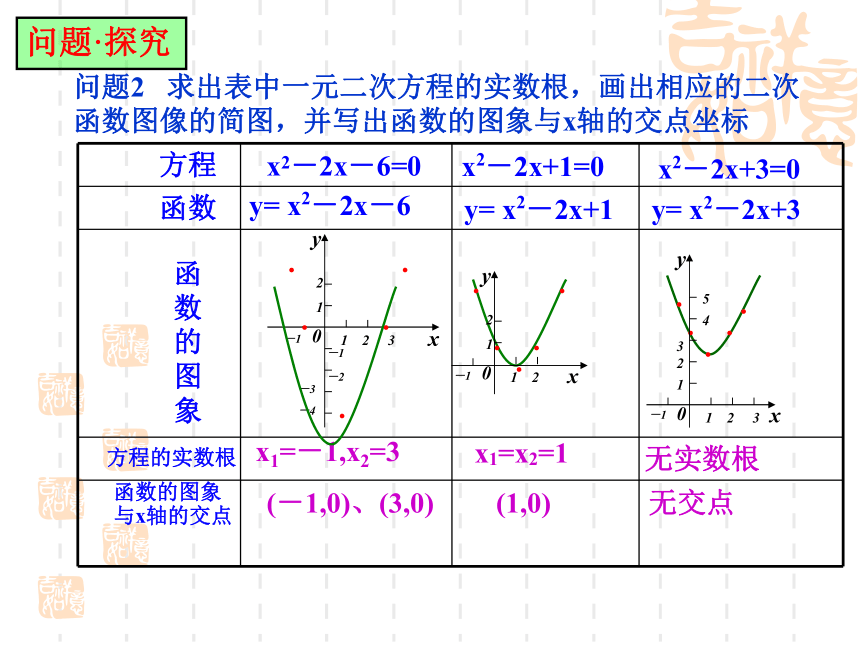
课件12张PPT。2.4.1 函数的零点 问题·探究方程x2-2x+1=0x2-2x+3=0y= x2-2x-6y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-6=0y= x2-2x+3问题·探究问题2 求出表中一元二次方程的实数根,画出相应的二次函数图像的简图,并写出函数的图象与x轴的交点坐标
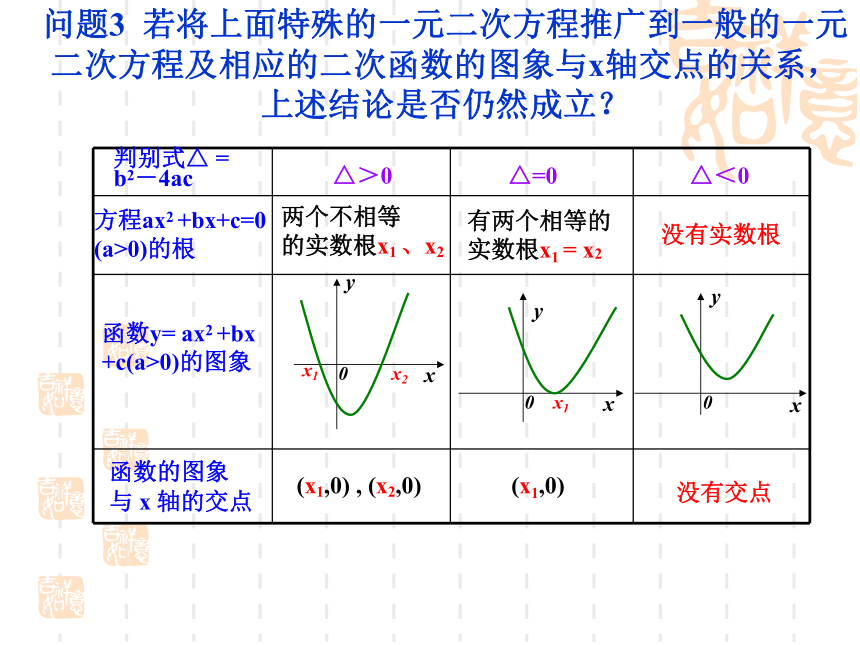
方程ax2 +bx+c=0
(a>0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
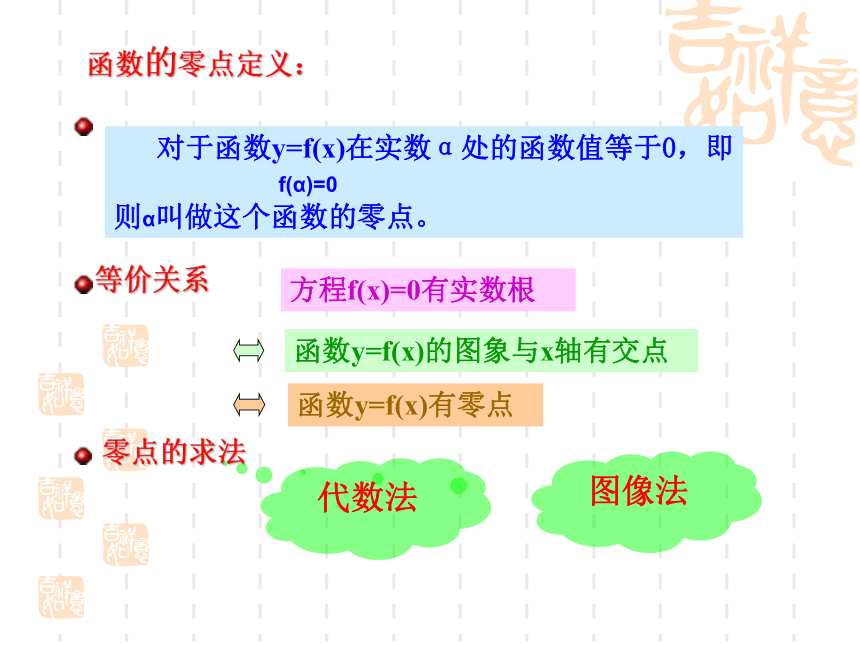
的实数根x1 、x2问题3 若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍然成立? 对于函数y=f(x)在实数α处的函数值等于0,即
f(α)=0
则α叫做这个函数的零点。方程f(x)=0有实数根函数的零点定义:等价关系零点的求法 代数法图像法二次函数零点的性质: 我们可以通过方程研究函数的性质在这4个区间内,取x的一些值,以及零点,列出这个函数的对应值表: 在坐标系内,描点连线,作出图像.
不难看出,函数图像经过三个零点时,函数值分别改变了符号,并且在每个区间内,函数值保持同号求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点反思小结:1.函数零点的定义
2.等价关系
3.求函数的零点 作业P75
习题2-4 A组 1,4,5
练习:P 72练习A,B再见
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-6=0y= x2-2x+3问题·探究问题2 求出表中一元二次方程的实数根,画出相应的二次函数图像的简图,并写出函数的图象与x轴的交点坐标
方程ax2 +bx+c=0
(a>0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2问题3 若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍然成立? 对于函数y=f(x)在实数α处的函数值等于0,即
f(α)=0
则α叫做这个函数的零点。方程f(x)=0有实数根函数的零点定义:等价关系零点的求法 代数法图像法二次函数零点的性质: 我们可以通过方程研究函数的性质在这4个区间内,取x的一些值,以及零点,列出这个函数的对应值表: 在坐标系内,描点连线,作出图像.
不难看出,函数图像经过三个零点时,函数值分别改变了符号,并且在每个区间内,函数值保持同号求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点反思小结:1.函数零点的定义
2.等价关系
3.求函数的零点 作业P75
习题2-4 A组 1,4,5
练习:P 72练习A,B再见
