(苏教版选修2-1)数学:第二章《单元综合》课件
文档属性
| 名称 | (苏教版选修2-1)数学:第二章《单元综合》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-22 12:30:00 | ||
图片预览





文档简介
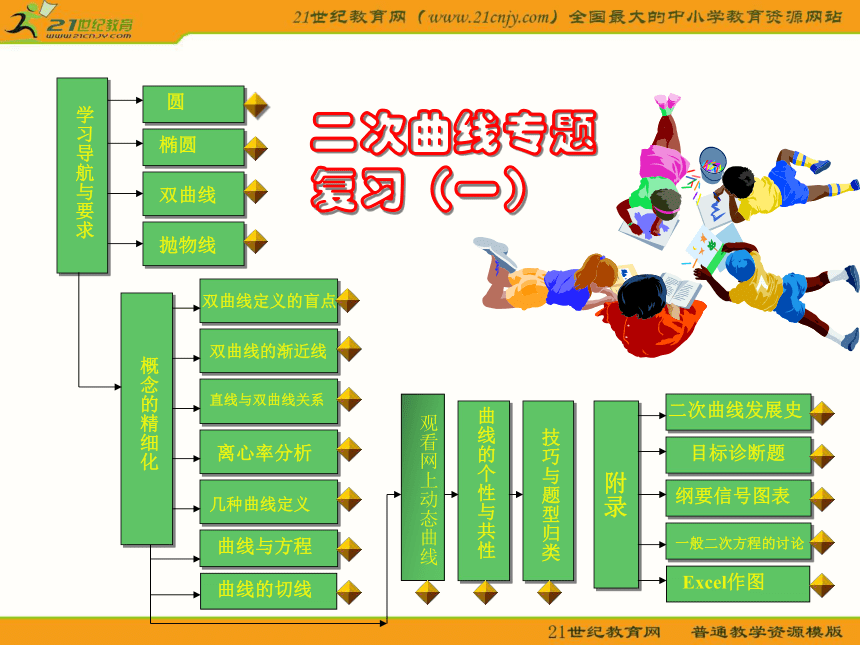
课件21张PPT。二次曲线专题(一)二次曲线专题复习(一)附录二次曲线发展史目标诊断题纲要信号图表学习导航与要求概念的精细化曲线的个性与共性技巧与题型归类圆椭圆双曲线双曲线抛物线双曲线定义的盲点双曲线的渐近线离心率分析直线与双曲线关系几种曲线定义一般二次方程的讨论曲线与方程Excel作图曲线的切线观看网上动态曲线圆的学习要求和导航学习要求:
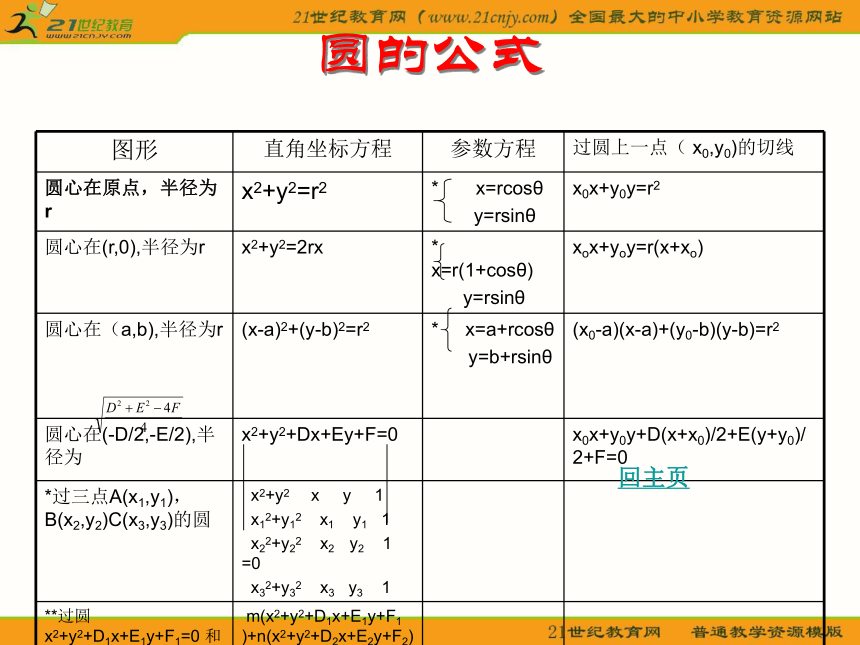
掌握由圆的定义推导圆的标准方程,理解参数 a,br的几何意义,掌握一般方程和标准方程的互化,用圆方程解决有关问题,解决直线与圆、圆与圆的位置关系。
学习导航:
圆的定义与标准方程 圆的几何定义
几何量间的关系d(P,M)=r 代数等式 (x-a)2+(y-b)2=r2 ,a,b,r的意义。
由(x-a)2+(y-b)2=r2 x2+y2+Dx+Ey
+F=0 且与Ax2+Bxy+Cy2+Dx+Ey+F=0比较,得出圆方程A=C≠0,B=0, 且D2+E2-4F>0
x2+y2+Dx+Ey+F=0的圆心(-D/2,-E/2)
半径 r=
圆与直线的关系,圆心M(a,b),半径r
直线 Ax+By+C=0,d>r相离,d=r相切,d 圆与圆关系
两圆的圆心(a1,b1),(a2,b2),两圆的半径r1,r1两圆的圆心距
关于相切: (1) 过圆上一点(x0,y0)
公式法: (x0-a)(x-a)+(y0-b)(y-b)=r2
判别式法:设切线y-y0=k(x-x0)代入圆方程,消去 y得相应x的二次方程,由判别式Δ=0可求得 k 从而得切线。
几何法:由圆心到切线距离r确定k而得切线 。
(2)圆外一点(x0,y0)的切线可仿上述判别式法、几何法处理。
继续圆的公式 回主页椭圆的学习要求与导航学习要求
知道椭圆定义并推出椭圆标准方程,理解参数a,b,c,e 的相互关系和几何意义。
能灵活应用椭圆定义、方程及性质解决问题(椭圆作图)。
学习导航
椭圆方程的定义及参数a,b,c,(e)是椭圆所特有的,与坐标无关。 a>b>0,c2=a2-b2,(e=c/a)必须牢固掌握。
椭圆的性质(有心、封闭的曲线),椭圆曲线的范围,掌握曲线(椭圆)对称性的判别,与坐标轴的交点。
特别:
1.椭圆的焦点一定在长轴上,
2. a,b,c三个参数的关系是满足以 a为斜边的 直角三角形勾股定理a2=b2+c2。
3.标准方程中a对应的变量x(或y),表明焦点就在x轴(或y轴)。
直线与椭圆的位置关系:
把直线与椭圆的方程组消元后得一元二次方程,它的判别式Δ>0直线与椭圆相交
Δ=0直线与椭圆相切
Δ <0直线与椭圆相离
继续椭圆的标准方程与性质回主页双曲线的学习要求和学习导航学习要求
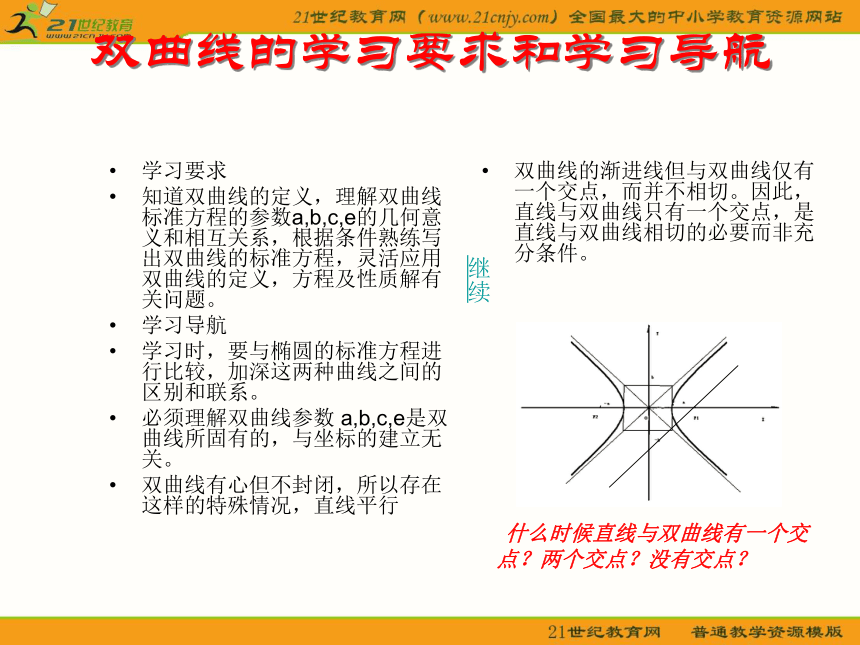
知道双曲线的定义,理解双曲线标准方程的参数a,b,c,e的几何意义和相互关系,根据条件熟练写出双曲线的标准方程,灵活应用双曲线的定义,方程及性质解有关问题。
学习导航
学习时,要与椭圆的标准方程进行比较,加深这两种曲线之间的区别和联系。
必须理解双曲线参数 a,b,c,e是双曲线所固有的,与坐标的建立无关。
双曲线有心但不封闭,所以存在这样的特殊情况,直线平行双曲线的渐进线但与双曲线仅有一个交点,而并不相切。因此,直线与双曲线只有一个交点,是直线与双曲线相切的必要而非充分条件。 什么时候直线与双曲线有一个交点?两个交点?没有交点?继续双曲线的标准方程与性质回主页双曲线定义的三个“盲点”双曲线定义:“平面内与两个定点F1F2的距离之差的绝对值是常量(小于|F1F2|)的点的轨迹叫做双曲线。”
定义内有三个盲点:“小于|F1F2|”, “绝对值”,“常数”,稍有不慎,就回出错。
盲点1:“小于|F1F2|”
将“小于|F1F2|”改成“大于|F1F2|”,经过演示,点的轨迹不存在。将“小于|F1F2|”改成“等于|F1F2|”,经过演示,点的轨迹不再是双曲线,而是以F1F2为起点的两条射线。
盲点2: “绝对值”
若将“绝对值”去掉,经过演示点的轨迹不再是两支曲线,只有一支,即左支或右支。
盲点3 :“常数”
若常数等于零,点的轨迹是什么?经过演示,不难发现点的轨迹是线段F1F2的中垂线。
思考题:
学习椭圆,抛物线的定义要注意什么?回主页双曲线与它的渐近线双曲线方程 可得
可以看出,随着 x无限变大,y也无限变大
所以双曲线是无界的,为了更好研究它无限
伸展的趋势,把上式改为
当x无限变大时, 趋近于0
这时,y就渐近于±b/a x,说明当x无限增大,
双曲线愈来愈接近直线y=± b/a x, 并且不论x
有多大,在第一象限内总有:
X无限变大,双曲线无限逼近渐近线,但永远
不会相连接。
设在第一象限内取x0 ,渐近线对应y1,双曲线
对应y0 ,有
说明了①在第一象限内,对同样的x渐近
线的值大于双曲线的值,②x无限增大, y1-y0 也无限趋向于0
思考题:
①你能说说离心率e与双曲线渐近线开口
大小的关系吗?
②你能举出其他已学的函数或方程的曲
线的渐近线的例子吗?回主页抛物线的学习要求和学习导航学习要求
掌握抛物线的定义,熟记四种标准方程,了解 焦参数 p 的几何意义,掌握抛物线的几何性质并能运用解决有关问题。
学习导航
掌握抛物线的定义,推导和建立抛物线的标准方程。用定义解题有时更简洁,虽然抛物线只一个参数,只须一个条件就可以求出,但有四个标准方程,所以必须掌握它的特征和对应的抛物线的开口方向,对称轴,焦点位置和准线的关系。
了解二次曲线的几种定义,对提高解题能力是有帮助的。
直线与抛物线的位置关系,特别注意相切的情况。由于抛物线与对称轴只一个交点,而它不是抛物线的切线, 所以直线与抛物线相切并不是直线
与抛物线只有一个公共点的充要条件。回主页继续坐标平移二次曲线Ax2+Bxy+Cy2+Dx+Ey+F=0
通过坐标平移可以消去一次项,简化方
程的表达式。
坐标系的改变,曲线的位置形状和大小
都没有改变,点的坐标和方程也随之改
变。
坐标的平移公式:x=x’+h x’=x-h
y=y’+k y’=y-k
主要题目类型:
1。已知原坐标系,新坐标原点,求一些点和方程的在新坐标系中的表达式。
2。已知新坐标系,原坐标的原点,求一些点和方程的在原坐标系中的表达式。
3。二次曲线方程经过配方成完全平方式
用平移公式简化。
4。把x=x’+h , y=y’+k 代入曲线方程,使一次项系数为0,简化曲线方程。回主页你还想学点吗?除了书本上二次曲线的定义外,还有一种统一的定义:平面上,一个动点到一个定点和一条定直线的距离之比是一个常数,动点的轨迹叫做圆锥曲线。这一定点叫做焦点,定直线叫做准线,这个常数叫做离心率。离心率小于1时叫做椭圆,离心率大于1时叫做双曲线,离心率等于1时叫做抛物线。
以焦点F为原点,经过焦点作准线l 的垂线为x轴,(取垂足到焦点的方向为正方向)建立直角坐标系。设焦点到准线的距离为p ,离心率为e,可得到直角坐标系中圆锥曲线的统一方程:
(1-e2)x2+y2-2e2px-e2p2=0又以焦点F为极点,经过焦点作准线l的垂线为极轴(取垂足到焦点的方向为正方向),建立极坐标系,得到极坐标系中圆锥曲线的统一方程
思考题
1,一个动点到两个定点(-3,0)(3,0)的斜率的积为-1,这轨迹是什么曲线?
若斜率的积为-1/4,是什么曲线?若斜率的积为1/4,是什么曲线?
2,一个动点到两个定点(-3,0)(3,0)的距离的平方差为常量,这轨迹是什么曲线?
:
回主页继续圆锥截线你还想学点吗?---离心率概念分析离心率是反映了二次曲线的形态及性质的重要概念。
引入定义:椭圆的焦距2c与长轴2a 的比叫做椭圆的离心率,类似的给出了双曲线,抛物线的离心率定义。
离心率定义 有两个要点:一个距离与长度有序之比,e=c/a>0
离心率取值范围:椭圆:2c<2a,故02a,得 e>1,按抛物线定义,e=1。
离心率与圆周率是几何中的两大比率,它们的共同特点:均为两个定量的有序之比,区别在于前者适用于二次曲线,后者只适用于圆;e值有相对的任意性(可变),π却具有唯一性(无理常数)。
离心率深刻揭示了二次曲线的实质,沟通了它们的关系。椭圆,双曲线,抛物线三者关系密切,是同一定义下的不同表现。三种曲线可统一定义为:平面内到一定点和一定直线的距离之比等于常数e的动点轨迹叫二次曲线。
建立适当的坐标,轨迹上任一点M(x,y),定点F(p,0)所以
整理即得
(1-e2)x2+y2-2px+p2=0当01方程分别是椭圆,抛物线,双曲线。
“对立统一,量变到质变”
e 0椭圆 圆,e 1,椭圆变得愈来愈扁,e=1为抛物线,e>1为双曲线,e 增大,则
b/a= 也变大,双曲线开口变大,反之,开口变小。 E趋向于1时,渐近线倾斜角近于0。
回主页圆锥曲线(圆锥截线) 点(点圆)圆椭圆双曲线抛物线圆锥曲线退化为两条直线,一条直线你能说出截面的条件吗?圆锥的顶角影响曲线形状吗?回主页继续二次曲线的发展史公元前四世纪,古希腊学者梅纳科莫斯最早通过截割圆锥的方法得到三种不同类型的曲线—椭圆(圆)、双曲线、抛物线,统称圆锥曲线。许多学者继续研究这一课题,最有成就的是生于小亚细亚佩加城的阿波罗尼,他将自已的成果写成八大卷的《圆锥曲线论》,成为这一课题的经典文献。
十六世纪,著名天文学家开普勒发现行星按椭圆形轨道运行,著名天文学家伽里略证明了不计阻力的斜抛运动的轨迹是抛物线。这说明了圆锥曲线并不是附生于圆锥之上的静态曲线,而是自然界中物体常见的运动形式。
1629年,法国数学家费马在《平面和立体轨迹引论》一书中,运用斜角坐标研究圆锥曲线,证明了圆锥曲线的方程都是含有二个未知数且最高次幂是二次的方程。反之,一般二元二次方程点的轨迹是圆锥曲线。1655年,英国数学家沃利斯在《圆锥截线论》中,干脆把圆锥曲线叫作二次曲线。
1748年,著名数学家欧拉在《无穷小分析引论》一文中,详细讨论了形如:Ax2+Bxy+Cy2+Dx+Ey+F=0
的一般二次方程,证明经过平移、转轴变换,任何一个二次方程可以化为椭圆(圆)、双曲线、抛物线及它们的退化形式,所以二次曲线就是圆锥曲线。回主页椭圆双曲线抛物线基本性质回主页一些常用技能技巧的梳理在巩固求曲线方程、应用曲线方程的基础上,练习常用的技能技巧,提高解题能力。
建立适当的坐标系
应用解几方法解题,必须建立坐标系,而且选定恰当的坐标系(一般是以原点、坐标轴对称的,或以原点为起点),简化曲线方程。
2.充分利用圆锥曲线特有的几何性质。
例如:m为何值时,直线2x-y+m=0和圆x2+y2=5①无公共点?②截得弦长为2?③交点处两条半径互相垂直?
解:圆心(0,0)到直线距离d=
圆半径r= ,① 时即m<-5或m>5时圆和直线无公共点。②∵弦过中点的半径垂直于弦∴r2-d2=1即5-m2/5=1∴当m=± 时圆在直线上截得弦长为2 ③此时弦与过弦两端的半径组成等腰直角三角形
∴
时过弦两端的半径互相垂直。
3 .圆锥曲线定义的应用
有些题目从表象上看较难,但用圆锥曲
线定义解题,问题迎刃而解。
继续一些常用技能技巧的梳理如图
双曲线方程 的左焦点作弦交曲线于A,B,连接AF2和 BF2,求|AF2|+|BF2|-|AB| 的值
解:||AF2|-|AF1||=2a=8, ||BF2|-|BF1||=2a=8, |AF2|+|BF2|-|AB| 的值为16。
曲线系方程的应用
方程f1(x,y)+λf2(x,y)=0表示的曲线经过曲线f1(x,y)=0和曲线f2(x,y)=0的交点(A1x+B1y+C1)+λ(A2x+B2y+C2)=0表示过直线A1x+B1y+C1=0,A2x+
B2y+C2=0的 交点的一系列直线。
你能写出圆系列方程和双曲线系列方程吗?
例题:一个圆经过已知圆x2+y2-x+y-2=0和x2+y2=5的交点,且圆心在直线3x+4y-1=0上求圆方程。
解:设所求圆方程为( x2+y2-x+y-2)+ λ(x2+y2-5)=0即
(1+λ)x2+(1+λ)y2-x+y-(2+λ)=0
其圆心为(1/(2+2λ),-1/(2+2λ))
在已知直线上,
得λ=-1.5,所求方程为:
X2+y2+2x-2y-11=0前一页继续一些常用技能技巧的梳理韦达定理的应用:
例题1:已知直线l 过(1,0)点,倾斜角为π/4,求 l在椭圆x2+2y2=4 上截得的长?
解:直线方程为y=x-1代入椭圆方程x2+2y2=4 ,得3 x2 -4x-2=0
设所截交点为AB
|AB|2 =(x2-x1)2+(y2-y1)2
=2(x2-x1)2
=2((x2+x1)2 -4 x2x1 )
=80/9
|AB|=回主页继续一般二次方程的讨论一般二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0经过旋转变换,适当选取θ角,化成
A’x’2+C’y’2+D’x’+E’y’+F’=0
关键看A’C’是否有一个为零?都不为零时它们是同号还是异号来决定。经过变换,-4A’C’=B2-4AC。Δ= B2-4AC为二次方程判别式。
回主页
掌握由圆的定义推导圆的标准方程,理解参数 a,br的几何意义,掌握一般方程和标准方程的互化,用圆方程解决有关问题,解决直线与圆、圆与圆的位置关系。
学习导航:
圆的定义与标准方程 圆的几何定义
几何量间的关系d(P,M)=r 代数等式 (x-a)2+(y-b)2=r2 ,a,b,r的意义。
由(x-a)2+(y-b)2=r2 x2+y2+Dx+Ey
+F=0 且与Ax2+Bxy+Cy2+Dx+Ey+F=0比较,得出圆方程A=C≠0,B=0, 且D2+E2-4F>0
x2+y2+Dx+Ey+F=0的圆心(-D/2,-E/2)
半径 r=
圆与直线的关系,圆心M(a,b),半径r
直线 Ax+By+C=0,d>r相离,d=r相切,d
两圆的圆心(a1,b1),(a2,b2),两圆的半径r1,r1两圆的圆心距
关于相切: (1) 过圆上一点(x0,y0)
公式法: (x0-a)(x-a)+(y0-b)(y-b)=r2
判别式法:设切线y-y0=k(x-x0)代入圆方程,消去 y得相应x的二次方程,由判别式Δ=0可求得 k 从而得切线。
几何法:由圆心到切线距离r确定k而得切线 。
(2)圆外一点(x0,y0)的切线可仿上述判别式法、几何法处理。
继续圆的公式 回主页椭圆的学习要求与导航学习要求
知道椭圆定义并推出椭圆标准方程,理解参数a,b,c,e 的相互关系和几何意义。
能灵活应用椭圆定义、方程及性质解决问题(椭圆作图)。
学习导航
椭圆方程的定义及参数a,b,c,(e)是椭圆所特有的,与坐标无关。 a>b>0,c2=a2-b2,(e=c/a)必须牢固掌握。
椭圆的性质(有心、封闭的曲线),椭圆曲线的范围,掌握曲线(椭圆)对称性的判别,与坐标轴的交点。
特别:
1.椭圆的焦点一定在长轴上,
2. a,b,c三个参数的关系是满足以 a为斜边的 直角三角形勾股定理a2=b2+c2。
3.标准方程中a对应的变量x(或y),表明焦点就在x轴(或y轴)。
直线与椭圆的位置关系:
把直线与椭圆的方程组消元后得一元二次方程,它的判别式Δ>0直线与椭圆相交
Δ=0直线与椭圆相切
Δ <0直线与椭圆相离
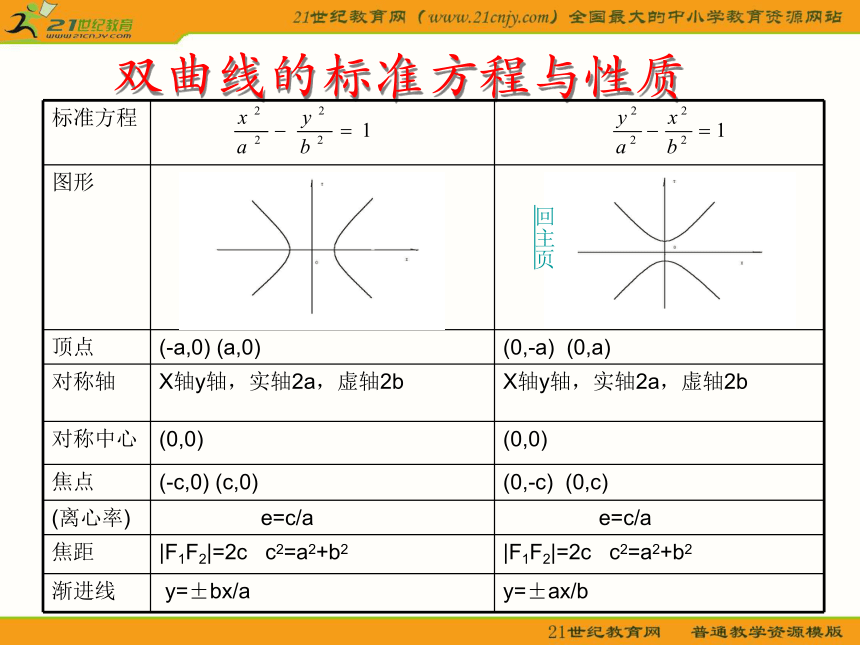
继续椭圆的标准方程与性质回主页双曲线的学习要求和学习导航学习要求
知道双曲线的定义,理解双曲线标准方程的参数a,b,c,e的几何意义和相互关系,根据条件熟练写出双曲线的标准方程,灵活应用双曲线的定义,方程及性质解有关问题。
学习导航
学习时,要与椭圆的标准方程进行比较,加深这两种曲线之间的区别和联系。
必须理解双曲线参数 a,b,c,e是双曲线所固有的,与坐标的建立无关。
双曲线有心但不封闭,所以存在这样的特殊情况,直线平行双曲线的渐进线但与双曲线仅有一个交点,而并不相切。因此,直线与双曲线只有一个交点,是直线与双曲线相切的必要而非充分条件。 什么时候直线与双曲线有一个交点?两个交点?没有交点?继续双曲线的标准方程与性质回主页双曲线定义的三个“盲点”双曲线定义:“平面内与两个定点F1F2的距离之差的绝对值是常量(小于|F1F2|)的点的轨迹叫做双曲线。”
定义内有三个盲点:“小于|F1F2|”, “绝对值”,“常数”,稍有不慎,就回出错。
盲点1:“小于|F1F2|”
将“小于|F1F2|”改成“大于|F1F2|”,经过演示,点的轨迹不存在。将“小于|F1F2|”改成“等于|F1F2|”,经过演示,点的轨迹不再是双曲线,而是以F1F2为起点的两条射线。
盲点2: “绝对值”
若将“绝对值”去掉,经过演示点的轨迹不再是两支曲线,只有一支,即左支或右支。
盲点3 :“常数”
若常数等于零,点的轨迹是什么?经过演示,不难发现点的轨迹是线段F1F2的中垂线。
思考题:
学习椭圆,抛物线的定义要注意什么?回主页双曲线与它的渐近线双曲线方程 可得
可以看出,随着 x无限变大,y也无限变大
所以双曲线是无界的,为了更好研究它无限
伸展的趋势,把上式改为
当x无限变大时, 趋近于0
这时,y就渐近于±b/a x,说明当x无限增大,
双曲线愈来愈接近直线y=± b/a x, 并且不论x
有多大,在第一象限内总有:
X无限变大,双曲线无限逼近渐近线,但永远
不会相连接。
设在第一象限内取x0 ,渐近线对应y1,双曲线
对应y0 ,有
说明了①在第一象限内,对同样的x渐近
线的值大于双曲线的值,②x无限增大, y1-y0 也无限趋向于0
思考题:
①你能说说离心率e与双曲线渐近线开口
大小的关系吗?
②你能举出其他已学的函数或方程的曲
线的渐近线的例子吗?回主页抛物线的学习要求和学习导航学习要求
掌握抛物线的定义,熟记四种标准方程,了解 焦参数 p 的几何意义,掌握抛物线的几何性质并能运用解决有关问题。
学习导航
掌握抛物线的定义,推导和建立抛物线的标准方程。用定义解题有时更简洁,虽然抛物线只一个参数,只须一个条件就可以求出,但有四个标准方程,所以必须掌握它的特征和对应的抛物线的开口方向,对称轴,焦点位置和准线的关系。
了解二次曲线的几种定义,对提高解题能力是有帮助的。
直线与抛物线的位置关系,特别注意相切的情况。由于抛物线与对称轴只一个交点,而它不是抛物线的切线, 所以直线与抛物线相切并不是直线
与抛物线只有一个公共点的充要条件。回主页继续坐标平移二次曲线Ax2+Bxy+Cy2+Dx+Ey+F=0
通过坐标平移可以消去一次项,简化方
程的表达式。
坐标系的改变,曲线的位置形状和大小
都没有改变,点的坐标和方程也随之改
变。
坐标的平移公式:x=x’+h x’=x-h
y=y’+k y’=y-k
主要题目类型:
1。已知原坐标系,新坐标原点,求一些点和方程的在新坐标系中的表达式。
2。已知新坐标系,原坐标的原点,求一些点和方程的在原坐标系中的表达式。
3。二次曲线方程经过配方成完全平方式
用平移公式简化。
4。把x=x’+h , y=y’+k 代入曲线方程,使一次项系数为0,简化曲线方程。回主页你还想学点吗?除了书本上二次曲线的定义外,还有一种统一的定义:平面上,一个动点到一个定点和一条定直线的距离之比是一个常数,动点的轨迹叫做圆锥曲线。这一定点叫做焦点,定直线叫做准线,这个常数叫做离心率。离心率小于1时叫做椭圆,离心率大于1时叫做双曲线,离心率等于1时叫做抛物线。
以焦点F为原点,经过焦点作准线l 的垂线为x轴,(取垂足到焦点的方向为正方向)建立直角坐标系。设焦点到准线的距离为p ,离心率为e,可得到直角坐标系中圆锥曲线的统一方程:
(1-e2)x2+y2-2e2px-e2p2=0又以焦点F为极点,经过焦点作准线l的垂线为极轴(取垂足到焦点的方向为正方向),建立极坐标系,得到极坐标系中圆锥曲线的统一方程
思考题
1,一个动点到两个定点(-3,0)(3,0)的斜率的积为-1,这轨迹是什么曲线?
若斜率的积为-1/4,是什么曲线?若斜率的积为1/4,是什么曲线?
2,一个动点到两个定点(-3,0)(3,0)的距离的平方差为常量,这轨迹是什么曲线?
:
回主页继续圆锥截线你还想学点吗?---离心率概念分析离心率是反映了二次曲线的形态及性质的重要概念。
引入定义:椭圆的焦距2c与长轴2a 的比叫做椭圆的离心率,类似的给出了双曲线,抛物线的离心率定义。
离心率定义 有两个要点:一个距离与长度有序之比,e=c/a>0
离心率取值范围:椭圆:2c<2a,故0
离心率与圆周率是几何中的两大比率,它们的共同特点:均为两个定量的有序之比,区别在于前者适用于二次曲线,后者只适用于圆;e值有相对的任意性(可变),π却具有唯一性(无理常数)。
离心率深刻揭示了二次曲线的实质,沟通了它们的关系。椭圆,双曲线,抛物线三者关系密切,是同一定义下的不同表现。三种曲线可统一定义为:平面内到一定点和一定直线的距离之比等于常数e的动点轨迹叫二次曲线。
建立适当的坐标,轨迹上任一点M(x,y),定点F(p,0)所以
整理即得
(1-e2)x2+y2-2px+p2=0当0
“对立统一,量变到质变”
e 0椭圆 圆,e 1,椭圆变得愈来愈扁,e=1为抛物线,e>1为双曲线,e 增大,则
b/a= 也变大,双曲线开口变大,反之,开口变小。 E趋向于1时,渐近线倾斜角近于0。
回主页圆锥曲线(圆锥截线) 点(点圆)圆椭圆双曲线抛物线圆锥曲线退化为两条直线,一条直线你能说出截面的条件吗?圆锥的顶角影响曲线形状吗?回主页继续二次曲线的发展史公元前四世纪,古希腊学者梅纳科莫斯最早通过截割圆锥的方法得到三种不同类型的曲线—椭圆(圆)、双曲线、抛物线,统称圆锥曲线。许多学者继续研究这一课题,最有成就的是生于小亚细亚佩加城的阿波罗尼,他将自已的成果写成八大卷的《圆锥曲线论》,成为这一课题的经典文献。
十六世纪,著名天文学家开普勒发现行星按椭圆形轨道运行,著名天文学家伽里略证明了不计阻力的斜抛运动的轨迹是抛物线。这说明了圆锥曲线并不是附生于圆锥之上的静态曲线,而是自然界中物体常见的运动形式。
1629年,法国数学家费马在《平面和立体轨迹引论》一书中,运用斜角坐标研究圆锥曲线,证明了圆锥曲线的方程都是含有二个未知数且最高次幂是二次的方程。反之,一般二元二次方程点的轨迹是圆锥曲线。1655年,英国数学家沃利斯在《圆锥截线论》中,干脆把圆锥曲线叫作二次曲线。
1748年,著名数学家欧拉在《无穷小分析引论》一文中,详细讨论了形如:Ax2+Bxy+Cy2+Dx+Ey+F=0
的一般二次方程,证明经过平移、转轴变换,任何一个二次方程可以化为椭圆(圆)、双曲线、抛物线及它们的退化形式,所以二次曲线就是圆锥曲线。回主页椭圆双曲线抛物线基本性质回主页一些常用技能技巧的梳理在巩固求曲线方程、应用曲线方程的基础上,练习常用的技能技巧,提高解题能力。
建立适当的坐标系
应用解几方法解题,必须建立坐标系,而且选定恰当的坐标系(一般是以原点、坐标轴对称的,或以原点为起点),简化曲线方程。
2.充分利用圆锥曲线特有的几何性质。
例如:m为何值时,直线2x-y+m=0和圆x2+y2=5①无公共点?②截得弦长为2?③交点处两条半径互相垂直?
解:圆心(0,0)到直线距离d=
圆半径r= ,① 时即m<-5或m>5时圆和直线无公共点。②∵弦过中点的半径垂直于弦∴r2-d2=1即5-m2/5=1∴当m=± 时圆在直线上截得弦长为2 ③此时弦与过弦两端的半径组成等腰直角三角形
∴
时过弦两端的半径互相垂直。
3 .圆锥曲线定义的应用
有些题目从表象上看较难,但用圆锥曲
线定义解题,问题迎刃而解。
继续一些常用技能技巧的梳理如图
双曲线方程 的左焦点作弦交曲线于A,B,连接AF2和 BF2,求|AF2|+|BF2|-|AB| 的值
解:||AF2|-|AF1||=2a=8, ||BF2|-|BF1||=2a=8, |AF2|+|BF2|-|AB| 的值为16。
曲线系方程的应用
方程f1(x,y)+λf2(x,y)=0表示的曲线经过曲线f1(x,y)=0和曲线f2(x,y)=0的交点(A1x+B1y+C1)+λ(A2x+B2y+C2)=0表示过直线A1x+B1y+C1=0,A2x+
B2y+C2=0的 交点的一系列直线。
你能写出圆系列方程和双曲线系列方程吗?
例题:一个圆经过已知圆x2+y2-x+y-2=0和x2+y2=5的交点,且圆心在直线3x+4y-1=0上求圆方程。
解:设所求圆方程为( x2+y2-x+y-2)+ λ(x2+y2-5)=0即
(1+λ)x2+(1+λ)y2-x+y-(2+λ)=0
其圆心为(1/(2+2λ),-1/(2+2λ))
在已知直线上,
得λ=-1.5,所求方程为:
X2+y2+2x-2y-11=0前一页继续一些常用技能技巧的梳理韦达定理的应用:
例题1:已知直线l 过(1,0)点,倾斜角为π/4,求 l在椭圆x2+2y2=4 上截得的长?
解:直线方程为y=x-1代入椭圆方程x2+2y2=4 ,得3 x2 -4x-2=0
设所截交点为AB
|AB|2 =(x2-x1)2+(y2-y1)2
=2(x2-x1)2
=2((x2+x1)2 -4 x2x1 )
=80/9
|AB|=回主页继续一般二次方程的讨论一般二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0经过旋转变换,适当选取θ角,化成
A’x’2+C’y’2+D’x’+E’y’+F’=0
关键看A’C’是否有一个为零?都不为零时它们是同号还是异号来决定。经过变换,-4A’C’=B2-4AC。Δ= B2-4AC为二次方程判别式。
回主页
