(苏教版选修2-2)数学:1.1《平均变化率》课件
文档属性
| 名称 | (苏教版选修2-2)数学:1.1《平均变化率》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 67.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-22 12:30:00 | ||
图片预览





文档简介
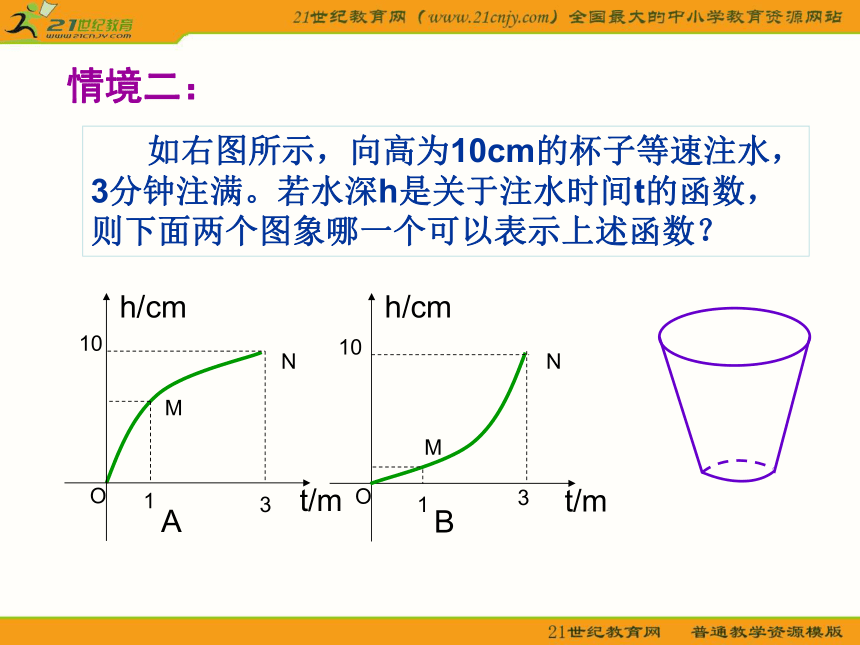
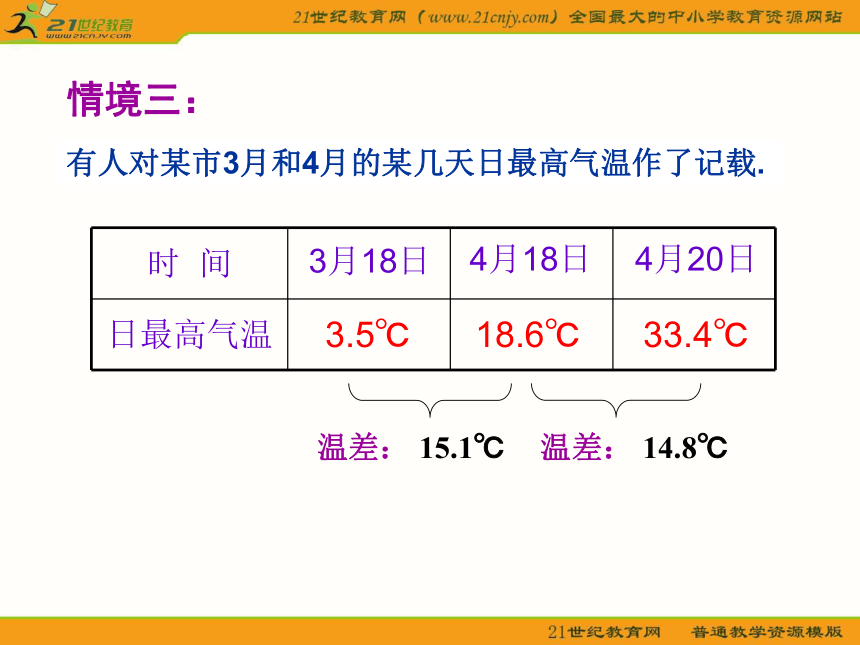
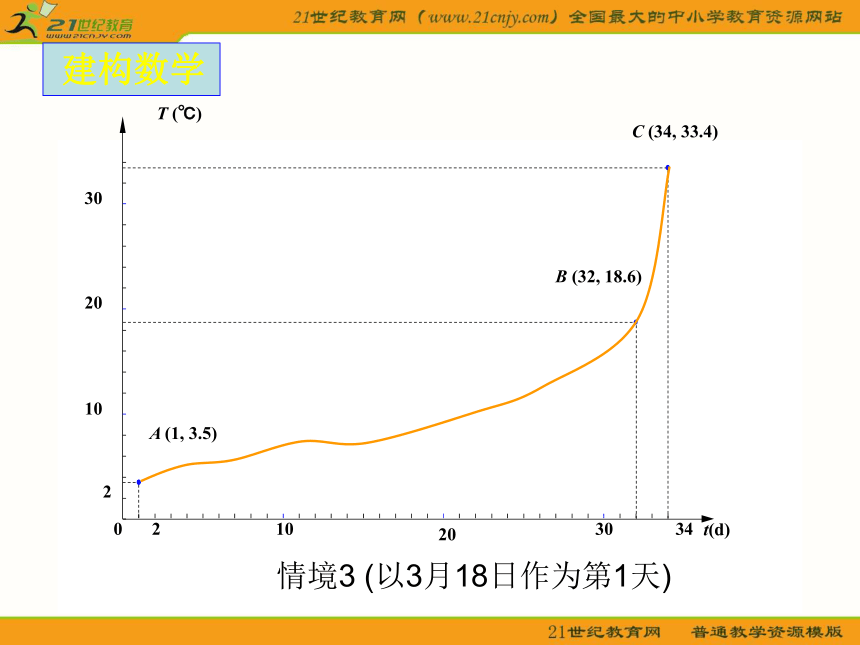
课件20张PPT。平均变化率 甲和乙投入相同资金经营同一商品,甲用1年时间挣到2万元, 乙用5个月时间挣到1万元。 从这样的数据看来,甲、 乙两人谁的经营成果更好?情境一:情境二: 如右图所示,向高为10cm的杯子等速注水,3分钟注满。若水深h是关于注水时间t的函数,则下面两个图象哪一个可以表示上述函数?MNMN有人对某市3月和4月的某几天日最高气温作了记载.温差: 15.1℃温差: 14.8℃情境三:3.5℃18.6℃33.4℃3月18日4月18日4月20日 如何用数学模型刻画变量变化的快与慢? 建构数学数缺形时少直观,
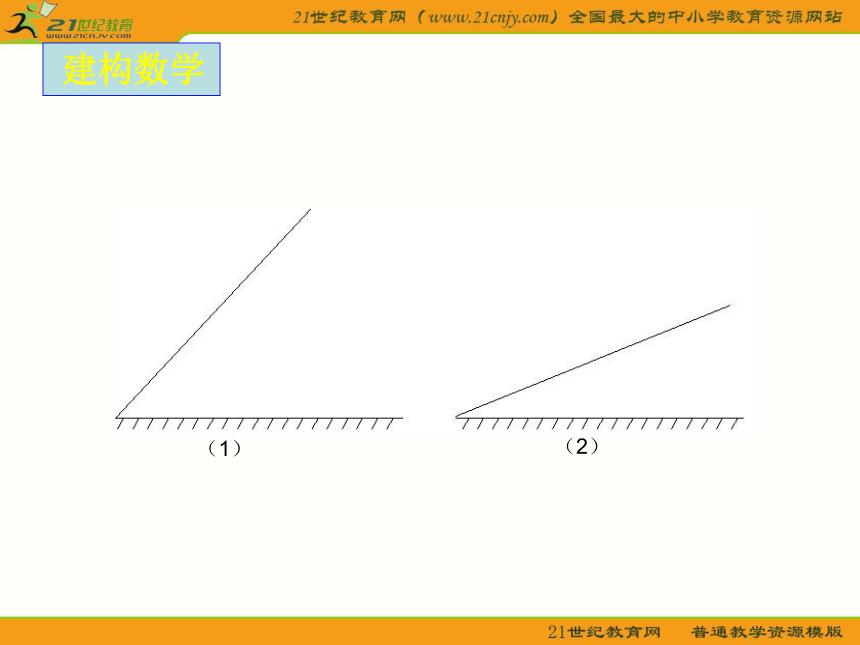
形缺数时难入微。华罗庚 如何量化曲线的陡峭程度?建构数学 建构数学 建构数学(以3月18日作为第1天)平均变化率 一般地,函数 在区间上 的平均变化率为 建构数学平均变化率是曲线陡峭程度的“数量化”;曲线陡峭程度是平均变化率的“视觉化”.平均变化率曲线陡峭程度数形变量变化的快慢 建构数学例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率。知识运用例2、水经过虹吸管从容器甲中流向容器乙,t s后
容器甲中水的体积 (单位: ),
计算第一个10s内容器甲中水的体积V的平均变化率。知识运用 第一个10s内V的平均
变化率为-0.3161cm3/s 第二个10s内V的平均
变化率为-0.1162cm3/s甲乙例3 已知函数 ,分别计算 在下
列区间上的平均变化率: (1)[1,3];
(2)[1,2];
(3)[1,1. 1];
(4)[1,1.001]。 432.12.001(5)[0.9,1];
(6)[0.99,1];
(7)[0.999,1].1.991.91.999知识运用例4、已知函数 分
别计算在区间[-3,-1],[0,5]上 及
的平均变化率。 y=kx+b在区间[m,n]上的平均变化率有什么特点? 知识运用 请分别计算出下面两个图象表示的函数h(t)在区间[0,3]上的平均变化率。知识运用课堂小结 今天这节课,你学到了
哪些知识?课堂小结平均变化率曲线陡峭程度数形变量变化的快慢课后作业1、国家环保局在规定的排污达标日期前,对甲乙两家企业进行检查,连续检测结果如图所示(其中W1(t),W 2(t) 分别表示甲乙两企业的排污量),试比较两个企业的治污效果。2、已知函数 ,分别计算函数f(x)在区间[1,3],[1,2],[1,1.1],[1,1.01]上的平均变化率。 思考:已知函数f(x)=x2,记In= ,n∈N*.
(1)求f(x)在区间In上的平均变化率an
(2)在数轴上画出数列{an}对应的点,并观察当n不断
增大时,an有什么变化趋势。
?
形缺数时难入微。华罗庚 如何量化曲线的陡峭程度?建构数学 建构数学 建构数学(以3月18日作为第1天)平均变化率 一般地,函数 在区间上 的平均变化率为 建构数学平均变化率是曲线陡峭程度的“数量化”;曲线陡峭程度是平均变化率的“视觉化”.平均变化率曲线陡峭程度数形变量变化的快慢 建构数学例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率。知识运用例2、水经过虹吸管从容器甲中流向容器乙,t s后
容器甲中水的体积 (单位: ),
计算第一个10s内容器甲中水的体积V的平均变化率。知识运用 第一个10s内V的平均
变化率为-0.3161cm3/s 第二个10s内V的平均
变化率为-0.1162cm3/s甲乙例3 已知函数 ,分别计算 在下
列区间上的平均变化率: (1)[1,3];
(2)[1,2];
(3)[1,1. 1];
(4)[1,1.001]。 432.12.001(5)[0.9,1];
(6)[0.99,1];
(7)[0.999,1].1.991.91.999知识运用例4、已知函数 分
别计算在区间[-3,-1],[0,5]上 及
的平均变化率。 y=kx+b在区间[m,n]上的平均变化率有什么特点? 知识运用 请分别计算出下面两个图象表示的函数h(t)在区间[0,3]上的平均变化率。知识运用课堂小结 今天这节课,你学到了
哪些知识?课堂小结平均变化率曲线陡峭程度数形变量变化的快慢课后作业1、国家环保局在规定的排污达标日期前,对甲乙两家企业进行检查,连续检测结果如图所示(其中W1(t),W 2(t) 分别表示甲乙两企业的排污量),试比较两个企业的治污效果。2、已知函数 ,分别计算函数f(x)在区间[1,3],[1,2],[1,1.1],[1,1.01]上的平均变化率。 思考:已知函数f(x)=x2,记In= ,n∈N*.
(1)求f(x)在区间In上的平均变化率an
(2)在数轴上画出数列{an}对应的点,并观察当n不断
增大时,an有什么变化趋势。
?
