(苏教版选修2-2)数学:1.3《函数的单调性与导数1》课件
文档属性
| 名称 | (苏教版选修2-2)数学:1.3《函数的单调性与导数1》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 77.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-22 12:30:00 | ||
图片预览




文档简介
课件18张PPT。数形变量变化的快慢知识回顾:函数单调性思考: 刻画函数变化趋势的是否还有其他…函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时函数单调性单调函数的图象特征1)都有 f ( x 1 ) < f ( x 2 ),则 f ( x ) 在G 上是增函数;2)都有 f ( x 1 ) > f ( x 2 ),则 f ( x ) 在G 上是减函数;增函数减函数G = ( a , b )导数与函数的单调性有什么关系?函数的单调性与导数讨论函数y=x2-4x+3的单调性. f(x1)-f(x2)=(x12-4x1+3)-(x22-4x2+3)
=(x1+x2)(x1-x2)-4(x1-x2)
= (x1-x2)(x1+x2-4)问题探究解:取x1f(x2),
那么 y=f(x)单调递减。
当20, f(x1) 那么 y=f(x)单调递增。综上 y=f(x)单调递增区间为(2,+∞)
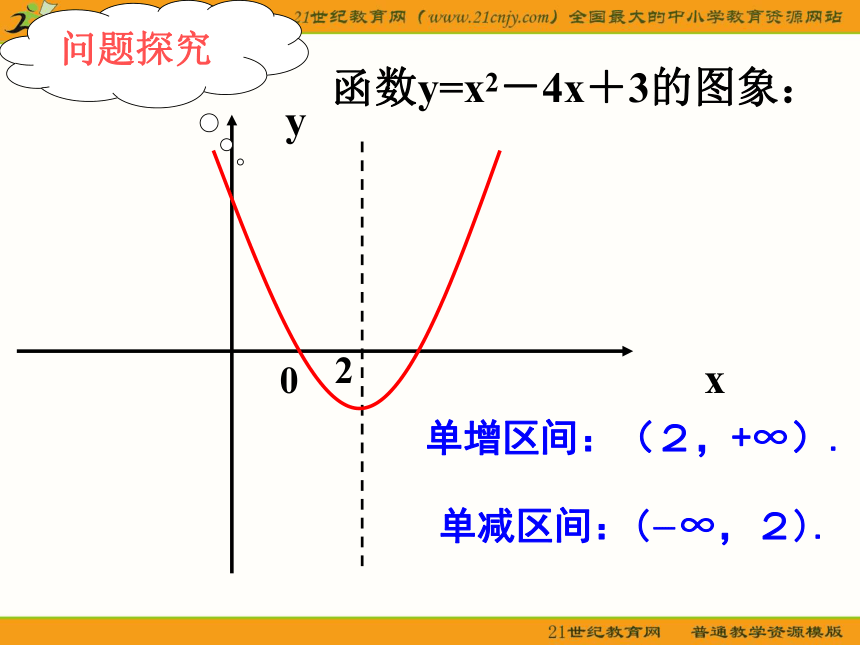
y=f(x)单调递减区间为(-∞,2)。函数y=x2-4x+3的图象:2单增区间:(2,+∞).单减区间:(-∞,2).问题探究2.......再观察函数y=x2-4x+3的图象 函数在区间
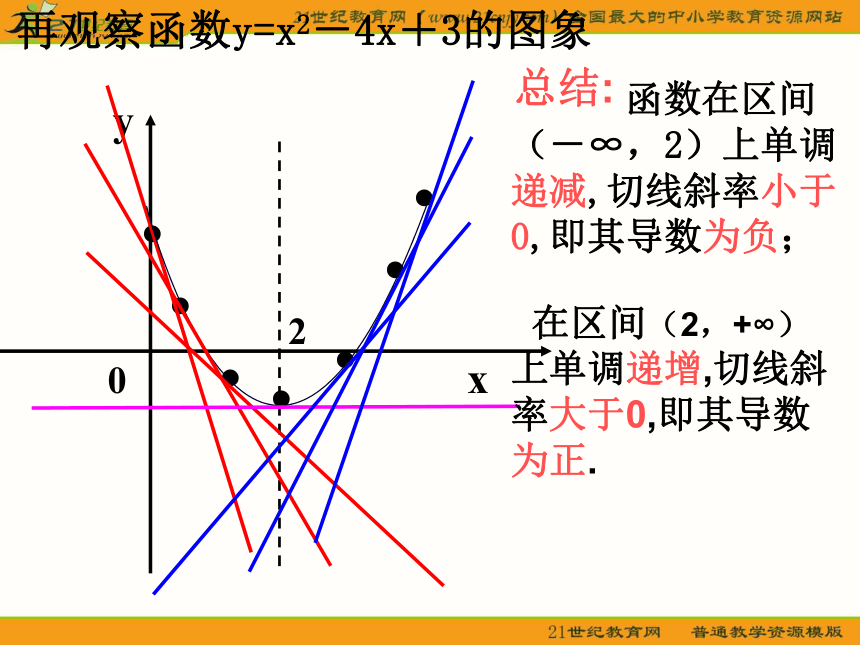
(-∞,2)上单调递减,切线斜率小于0,即其导数为负;总结: 在区间(2,+∞)上单调递增,切线斜率大于0,即其导数为正. 一般地,对于给定区间上的函数f(x),如果对于属于这个区间的任意两个自变量的值x1,x2,当x1 若f(x1) 内可导,则函数在该区间
如果f′(x)>0, 注意:如果在某个区间内恒有f′(x)=0,则f(x)为常数函数.如果f′(x)<0, 则f(x)为增函数;则f(x)为减函数.构建数学基本求导公式:忆一忆例:应用导数讨论函数y=x2-4x+3的
单调性.例:求函数f(x)=2x3-6x2+7的单调区间.解:函数的定义域为R,f′(x)=6x2-12x
令6x2-12x>0,解得x<0或x>2,
则f(x)的单增区间为(-∞,0)和
(2,+∞).
再令6x2-12x<0,解得0则f(x)的单减区间(0,2).注:当x=0或2时, f′(x)=0,即函数在该点单
调性发生改变.
例 求函数f(x)=sinx,x∈[0,2π]
的单调区间.知识应用应用导数求函数的单调区间(1).函数y=x-3在[-3,5]上为______函数(填“增”或“减”)。增求函数 的单调区间。已知导函数的下列信息:应用导数信息确定函数大致图象总结:根据导数确定函数的单调性1.确定函数f(x)的定义域.2.求出函数的导数.3.解不等式f ′(x)>0,得函数单增区间;
解不等式f′(x)<0,得函数单减区间.
=(x1+x2)(x1-x2)-4(x1-x2)
= (x1-x2)(x1+x2-4)问题探究解:取x1
那么 y=f(x)单调递减。
当2
y=f(x)单调递减区间为(-∞,2)。函数y=x2-4x+3的图象:2单增区间:(2,+∞).单减区间:(-∞,2).问题探究2.......再观察函数y=x2-4x+3的图象 函数在区间
(-∞,2)上单调递减,切线斜率小于0,即其导数为负;总结: 在区间(2,+∞)上单调递增,切线斜率大于0,即其导数为正. 一般地,对于给定区间上的函数f(x),如果对于属于这个区间的任意两个自变量的值x1,x2,当x1
如果f′(x)>0, 注意:如果在某个区间内恒有f′(x)=0,则f(x)为常数函数.如果f′(x)<0, 则f(x)为增函数;则f(x)为减函数.构建数学基本求导公式:忆一忆例:应用导数讨论函数y=x2-4x+3的
单调性.例:求函数f(x)=2x3-6x2+7的单调区间.解:函数的定义域为R,f′(x)=6x2-12x
令6x2-12x>0,解得x<0或x>2,
则f(x)的单增区间为(-∞,0)和
(2,+∞).
再令6x2-12x<0,解得0
调性发生改变.
例 求函数f(x)=sinx,x∈[0,2π]
的单调区间.知识应用应用导数求函数的单调区间(1).函数y=x-3在[-3,5]上为______函数(填“增”或“减”)。增求函数 的单调区间。已知导函数的下列信息:应用导数信息确定函数大致图象总结:根据导数确定函数的单调性1.确定函数f(x)的定义域.2.求出函数的导数.3.解不等式f ′(x)>0,得函数单增区间;
解不等式f′(x)<0,得函数单减区间.
