(苏教版选修2-2)数学:3.3《复数的几何意义》课件
文档属性
| 名称 | (苏教版选修2-2)数学:3.3《复数的几何意义》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 49.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-22 00:00:00 | ||
图片预览





文档简介
课件14张PPT。实数集的一些性质和特点:(1) 实数可以判定相等或不相等;(2) 不相等的实数可以比较大小;(3) 实数可以用数轴上的点表示;(4) 实数可以进行四则运算;(5) 负实数不能进行开偶次方根运算;……(1) 实数集原有的有关性质和特点能否
推广到复数集?(2)从复数的特点出发,寻找复数集新
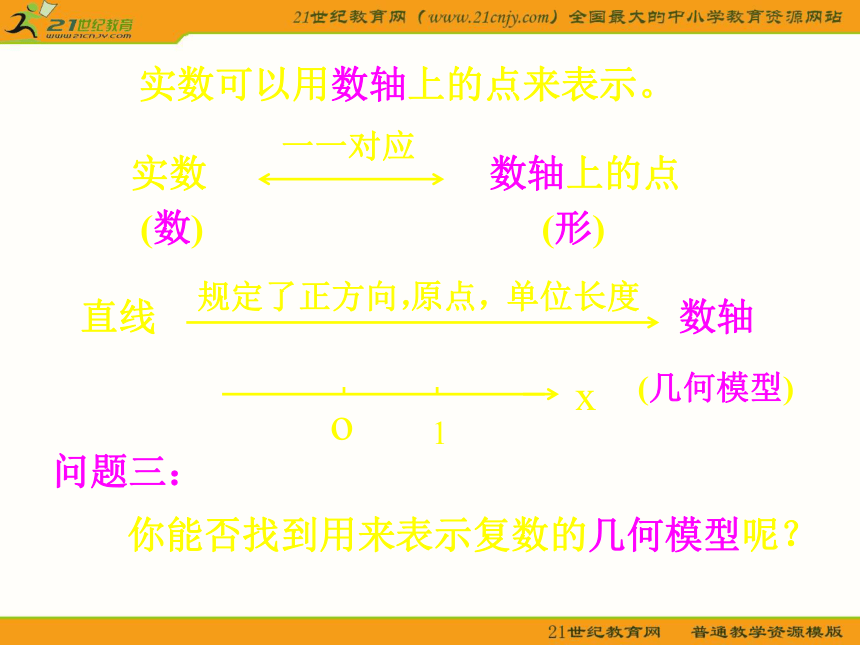
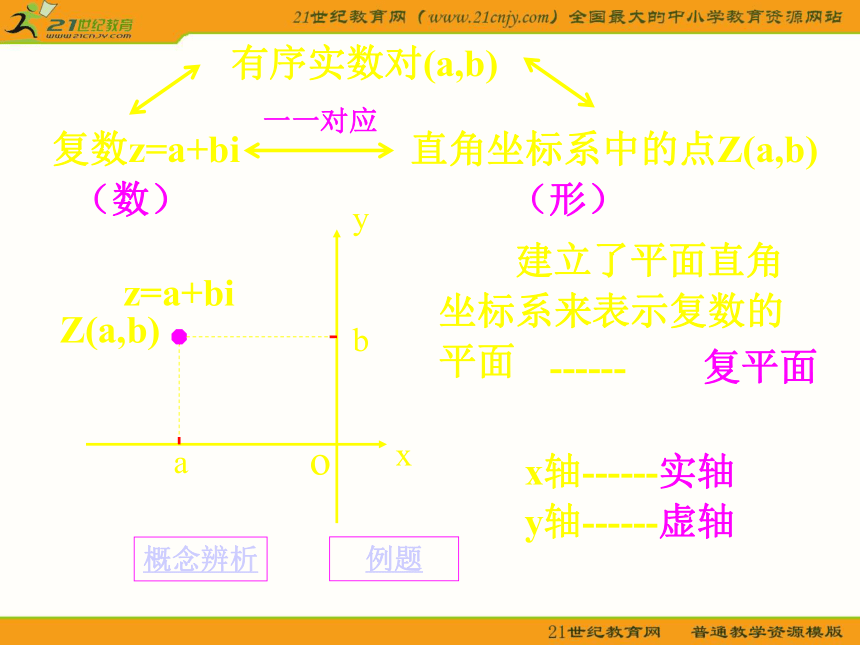
的(实数集所不具有)性质和特点?如何探索复数集的性质和特点?探索途径:复数的几何意义问题一问题二问题三问题四课堂小结问题一:你认为满足什么条件时,可以说这两个复数相等?对于复数a+bi和c+di(a,b,c,d ∈ R), a=c,并且b=d,即实部与虚部分别 相等时,叫这两个复数相等。记作a+bi=c+di。复数相等的内涵:复数a+bi可用有序实数对(a,b)表示。问题二: 任意两个复数可以比较大小吗?认为可以者,请拿出进行比较的方法;认为不可以者,请说明理由。xo1问题三: 你能否找到用来表示复数的几何模型呢?实数可以用数轴上的点来表示。一一对应 规定了正方向,直线数轴原点,单位长度实数 数轴上的点 (形)(数)(几何模型)复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------ 复平面一一对应z=a+bi概念辨析例题问题四:实数绝对值的几何意义:能否把绝对值概念推广到复数范围呢?XOAa| a | = | OA | 实数a在数轴上所对应的点A到原点O的距离。xOz=a+biy| z | = |OZ|复数的绝对值 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。(复数的模)的几何意义:Z (a,b) 例3 求下列复数的模:
(1)z1=-5i (2)z2=-3+4i (3)z3=5-5i(3)满足|z|=5(z∈C)的z值有几个?思考:(2)满足|z|=5(z∈R)的z值有几个?(4)z4=1+mi(m∈R) (5)z5=4a-3ai(a<0)(1)复数的模能否比较大小? 这些复 数对应的点在复平面上构成怎样的图形? 图示课堂小结:一. 数学知识:二. 数学思想:三. 数的发展和完善过程给我们的启示:(1)复平面(2)复数的模(3)类比思想(2)数形结合思想(1)转化思想课题:复数的有关概念(A)在复平面内,对应于实数的点都在实
轴上;
(B)在复平面内,对应于纯虚数的点都在
虚轴上;
(C)在复平面内,实轴上的点所对应的复
数都是实数;
(D)在复平面内,虚轴上的点所对应的复
数都是纯虚数。辨析:1.下列命题中的假命题是( )D 2.“a=0”是“复数a+bi (a , b∈R)所对应的点在虚轴上”的( )。
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)不充分不必要条件C例2 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。 变式:证明对一切m,此复数所对应的点不可能位于第四象限。解题思考:表示复数的点所在象限的问题复数的实部与虚部所满足的不等式组的问题转化(几何问题)(代数问题)一种重要的数学思想:数形结合思想xyO设z=x+yi(x,y∈R) 满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–5
推广到复数集?(2)从复数的特点出发,寻找复数集新
的(实数集所不具有)性质和特点?如何探索复数集的性质和特点?探索途径:复数的几何意义问题一问题二问题三问题四课堂小结问题一:你认为满足什么条件时,可以说这两个复数相等?对于复数a+bi和c+di(a,b,c,d ∈ R), a=c,并且b=d,即实部与虚部分别 相等时,叫这两个复数相等。记作a+bi=c+di。复数相等的内涵:复数a+bi可用有序实数对(a,b)表示。问题二: 任意两个复数可以比较大小吗?认为可以者,请拿出进行比较的方法;认为不可以者,请说明理由。xo1问题三: 你能否找到用来表示复数的几何模型呢?实数可以用数轴上的点来表示。一一对应 规定了正方向,直线数轴原点,单位长度实数 数轴上的点 (形)(数)(几何模型)复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------ 复平面一一对应z=a+bi概念辨析例题问题四:实数绝对值的几何意义:能否把绝对值概念推广到复数范围呢?XOAa| a | = | OA | 实数a在数轴上所对应的点A到原点O的距离。xOz=a+biy| z | = |OZ|复数的绝对值 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。(复数的模)的几何意义:Z (a,b) 例3 求下列复数的模:
(1)z1=-5i (2)z2=-3+4i (3)z3=5-5i(3)满足|z|=5(z∈C)的z值有几个?思考:(2)满足|z|=5(z∈R)的z值有几个?(4)z4=1+mi(m∈R) (5)z5=4a-3ai(a<0)(1)复数的模能否比较大小? 这些复 数对应的点在复平面上构成怎样的图形? 图示课堂小结:一. 数学知识:二. 数学思想:三. 数的发展和完善过程给我们的启示:(1)复平面(2)复数的模(3)类比思想(2)数形结合思想(1)转化思想课题:复数的有关概念(A)在复平面内,对应于实数的点都在实
轴上;
(B)在复平面内,对应于纯虚数的点都在
虚轴上;
(C)在复平面内,实轴上的点所对应的复
数都是实数;
(D)在复平面内,虚轴上的点所对应的复
数都是纯虚数。辨析:1.下列命题中的假命题是( )D 2.“a=0”是“复数a+bi (a , b∈R)所对应的点在虚轴上”的( )。
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)不充分不必要条件C例2 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。 变式:证明对一切m,此复数所对应的点不可能位于第四象限。解题思考:表示复数的点所在象限的问题复数的实部与虚部所满足的不等式组的问题转化(几何问题)(代数问题)一种重要的数学思想:数形结合思想xyO设z=x+yi(x,y∈R) 满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–5
