(苏教版选修2—2)数学:导数在实际生活的实际应用 同步练习
文档属性
| 名称 | (苏教版选修2—2)数学:导数在实际生活的实际应用 同步练习 | 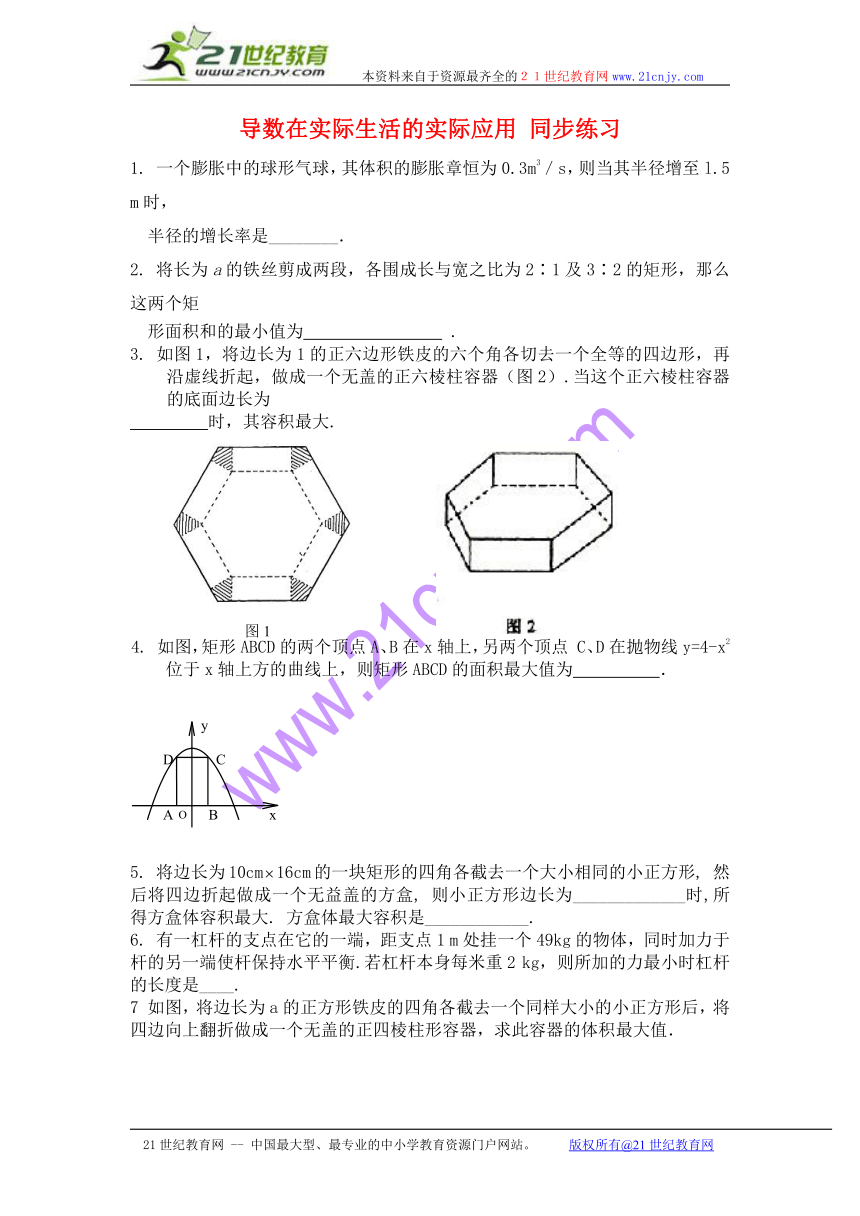 | |
| 格式 | rar | ||
| 文件大小 | 68.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-22 12:27:00 | ||
图片预览



文档简介
导数在实际生活的实际应用 同步练习
1. 一个膨胀中的球形气球,其体积的膨胀章恒为0.3m3/s,则当其半径增至l.5 m时,
半径的增长率是________.
2. 将长为a的铁丝剪成两段,各围成长与宽之比为2∶1及3∶2的矩形,那么这两个矩
形面积和的最小值为 .
3. 如图1,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器(图2).当这个正六棱柱容器的底面边长为
时,其容积最大.
21世纪教育网
4. 如图,矩形ABCD的两个顶点A、B在x轴上,另两个顶点 C、D在抛物线y=4-x2位于x轴上方的曲线上,则矩形ABCD的面积最大值为 .
5. 将边长为10cm16cm的一块矩形的四角各截去一个大小相同的小正方形, 然后将四边折起做成一个无益盖的方盒, 则小正方形边长为_____________时,所得方盒体容积最大. 方盒体最大容积是____________.
6. 有一杠杆的支点在它的一端,距支点1 m处挂一个49kg的物体,同时加力于杆的另一端使杆保持水平平衡.若杠杆本身每米重2 kg,则所加的力最小时杠杆的长度是____.
7 如图,将边长为a的正方形铁皮的四角各截去一个同样大小的小正方形后,将四边向上翻折做成一个无盖的正四棱柱形容器,求此容器的体积最大值.
8. (1) 求内接于半径为R的球并且体积最大的圆柱的高.[来源:21世纪教育网]
(2) 求内接于半径为R的球并且体积最大的圆锥的高.
9. 一人以3m/s的速度沿地面向高为100 m的建筑物走去,当此人距建筑物50 m时.他与建筑物顶部的距离改变率是多少?
10. 溶液自深度18 cm、顶部直径12 cm的圆锥形漏斗中,漏入一直径为10 cm的圆柱形
简中.开始时漏斗中盛满了水.已知当溶液在漏斗中的深度为12 cm时,其水面下落
的速度为1 cm/min,问:此时圆柱彤筒中,水面上升的速度为多少?
11. 一轮船以v km/h的速度航行,每小时用煤0. 3+0.001v3t重,问:v为何值时,才能使
轮船航行每千米用的煤最少?
12.用总长14.8m的钢条制作一个长方体容器的框架,若制作的容器的底面的一边长比另一边长0.5m.那么高为多少时,容器的容积最大?并求出它的最大容积?
13. 设工厂A到铁路线的垂直距离为20km, 垂足为B. 铁路线上距离B为100km处有一原料供应站C, 现要在铁路BC之间某处D修建一个原料中转站, 再由车站D向工厂修一条公路. 如果已知每千米的铁路运费与公路运费之比为3∶5, 那么D应选在何处, 才能使原料供应站C运货到工厂所需运费最省?
14. 甲乙两地相距SKm,汽车从甲地匀速行驶到乙地,速度不得超过CKm/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成; 可变部分与速度V(Km/h)的平方成正比比例系数为b, 固定成本为a.
(1)把全程运输成本y(元)表示为速度V(km/h)的函数, 并指出这个函数的定义域;
(2)为了使全程运输成本最小; 汽车应以多大的速度行驶.
21世纪教育网
参考答案
1.21世纪教育网
2.
3.
4.
5. 2cm,1444cm3.
6.7m.
7.
8. (1) 设圆柱的高为x, 则底面半径,圆柱的体积为
,(),∴令,[来源:21世纪教育网]
解得(负值舍去)因为只有一个极值点,所以当圆柱的高为时,
球内接圆柱的体积最大.
(2) 设圆锥的高为x, 则底面半径,圆锥的体积为
,(),∴令,
解得(负值舍去)因为只有一个极值点,所以当圆锥的高为时,球内接圆锥的体积最大.
9.
10.
11. 轮船航行每千米用的煤量,令,.
故v为何值时,才能使轮船航行每千米用的煤最少.
12. 【解析】设容器底面短边长为xm,则另一边为(x+0.5)m.于是高为
由和,得
设容器的容积为ym3,则有
整理得
∴
令,有
即,
解得 (舍去).
从而在定义域(0,1.6)内只有x=1处使.由题意,若x过小(接近0)或过大(接近1.6)时,y的值很小(接近0),因此,当x=1时,y取得最大值.
且y最大=,此时高为.
答案:容器的高为1.2m时容器的容积最大,最大容积为2.2m3.
13. 设BD之间的距离为xkm, 则,如果公路运费为a元/km, 那么铁路运费为元/km. 故从原料供应站C途经中转站D到工厂A所需运费为y,
∴ 令 解得舍去.
且是函数在定义域内唯一的极值点. 所以是函数最小值点.
由此可知, 车站D建于B,C之间且与B相距15km处时, 运费最省.
14. (1) 依题意可知,汽车从甲地匀速行驶到乙地所用的时间为,所以全程运输成本为:所以所求函数及其定义域为,;
(2) 函数的导数为,令
∴ ∴函数在区间是减函数;在区间是增函数,
所以 当时,行驶速度为;当时行驶速度为.
1. 一个膨胀中的球形气球,其体积的膨胀章恒为0.3m3/s,则当其半径增至l.5 m时,
半径的增长率是________.
2. 将长为a的铁丝剪成两段,各围成长与宽之比为2∶1及3∶2的矩形,那么这两个矩
形面积和的最小值为 .
3. 如图1,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器(图2).当这个正六棱柱容器的底面边长为
时,其容积最大.
21世纪教育网
4. 如图,矩形ABCD的两个顶点A、B在x轴上,另两个顶点 C、D在抛物线y=4-x2位于x轴上方的曲线上,则矩形ABCD的面积最大值为 .
5. 将边长为10cm16cm的一块矩形的四角各截去一个大小相同的小正方形, 然后将四边折起做成一个无益盖的方盒, 则小正方形边长为_____________时,所得方盒体容积最大. 方盒体最大容积是____________.
6. 有一杠杆的支点在它的一端,距支点1 m处挂一个49kg的物体,同时加力于杆的另一端使杆保持水平平衡.若杠杆本身每米重2 kg,则所加的力最小时杠杆的长度是____.
7 如图,将边长为a的正方形铁皮的四角各截去一个同样大小的小正方形后,将四边向上翻折做成一个无盖的正四棱柱形容器,求此容器的体积最大值.
8. (1) 求内接于半径为R的球并且体积最大的圆柱的高.[来源:21世纪教育网]
(2) 求内接于半径为R的球并且体积最大的圆锥的高.
9. 一人以3m/s的速度沿地面向高为100 m的建筑物走去,当此人距建筑物50 m时.他与建筑物顶部的距离改变率是多少?
10. 溶液自深度18 cm、顶部直径12 cm的圆锥形漏斗中,漏入一直径为10 cm的圆柱形
简中.开始时漏斗中盛满了水.已知当溶液在漏斗中的深度为12 cm时,其水面下落
的速度为1 cm/min,问:此时圆柱彤筒中,水面上升的速度为多少?
11. 一轮船以v km/h的速度航行,每小时用煤0. 3+0.001v3t重,问:v为何值时,才能使
轮船航行每千米用的煤最少?
12.用总长14.8m的钢条制作一个长方体容器的框架,若制作的容器的底面的一边长比另一边长0.5m.那么高为多少时,容器的容积最大?并求出它的最大容积?
13. 设工厂A到铁路线的垂直距离为20km, 垂足为B. 铁路线上距离B为100km处有一原料供应站C, 现要在铁路BC之间某处D修建一个原料中转站, 再由车站D向工厂修一条公路. 如果已知每千米的铁路运费与公路运费之比为3∶5, 那么D应选在何处, 才能使原料供应站C运货到工厂所需运费最省?
14. 甲乙两地相距SKm,汽车从甲地匀速行驶到乙地,速度不得超过CKm/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成; 可变部分与速度V(Km/h)的平方成正比比例系数为b, 固定成本为a.
(1)把全程运输成本y(元)表示为速度V(km/h)的函数, 并指出这个函数的定义域;
(2)为了使全程运输成本最小; 汽车应以多大的速度行驶.
21世纪教育网
参考答案
1.21世纪教育网
2.
3.
4.
5. 2cm,1444cm3.
6.7m.
7.
8. (1) 设圆柱的高为x, 则底面半径,圆柱的体积为
,(),∴令,[来源:21世纪教育网]
解得(负值舍去)因为只有一个极值点,所以当圆柱的高为时,
球内接圆柱的体积最大.
(2) 设圆锥的高为x, 则底面半径,圆锥的体积为
,(),∴令,
解得(负值舍去)因为只有一个极值点,所以当圆锥的高为时,球内接圆锥的体积最大.
9.
10.
11. 轮船航行每千米用的煤量,令,.
故v为何值时,才能使轮船航行每千米用的煤最少.
12. 【解析】设容器底面短边长为xm,则另一边为(x+0.5)m.于是高为
由和,得
设容器的容积为ym3,则有
整理得
∴
令,有
即,
解得 (舍去).
从而在定义域(0,1.6)内只有x=1处使.由题意,若x过小(接近0)或过大(接近1.6)时,y的值很小(接近0),因此,当x=1时,y取得最大值.
且y最大=,此时高为.
答案:容器的高为1.2m时容器的容积最大,最大容积为2.2m3.
13. 设BD之间的距离为xkm, 则,如果公路运费为a元/km, 那么铁路运费为元/km. 故从原料供应站C途经中转站D到工厂A所需运费为y,
∴ 令 解得舍去.
且是函数在定义域内唯一的极值点. 所以是函数最小值点.
由此可知, 车站D建于B,C之间且与B相距15km处时, 运费最省.
14. (1) 依题意可知,汽车从甲地匀速行驶到乙地所用的时间为,所以全程运输成本为:所以所求函数及其定义域为,;
(2) 函数的导数为,令
∴ ∴函数在区间是减函数;在区间是增函数,
所以 当时,行驶速度为;当时行驶速度为.
