幂函数 (1)

课件21张PPT。幂 函 数我们先来看看几个具体的问题: (1)如果张红买了每千克1元的蔬菜W千克,那么她需要支付
__________
P=W 元(2)如果正方形的边长为 a,那么正方形的面积_____(3)如果立方体的边长为a,那么立方体的体积___________
(4)如果某人 t s内骑车行进1 km,那么他骑车的平均速度___
_____________
p是w的函数S=a2 S 是a的函数V=a3 V是a的函数V=t?1 km/s V是t 的函数一 引入以上问题中的函数有什么共同特征？（1）都是函数；
（2）均是以自变量为底的幂；
（3）指数为常数；
（4）自变量前的系数为1;
（5）幂前的系数也为1。
上述问题中涉及的函数，都是形如y=xa的函数。1。幂函数的定义：形如 y = xa 的函数叫做幂函数，
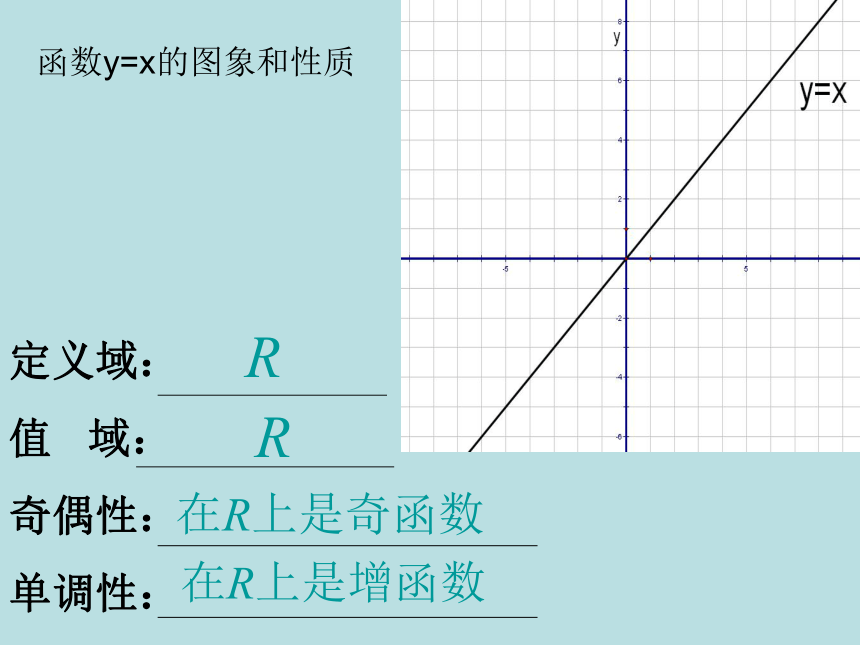
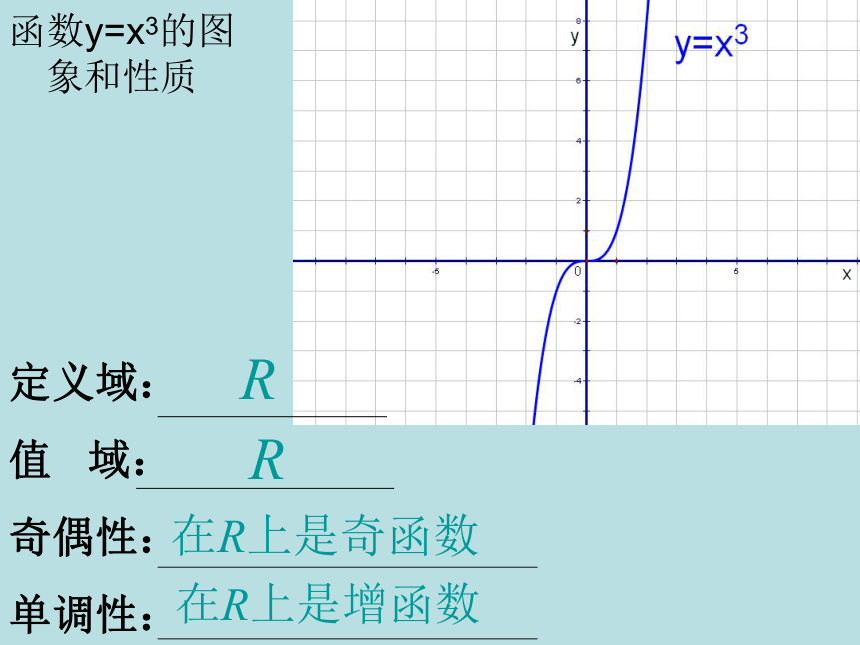
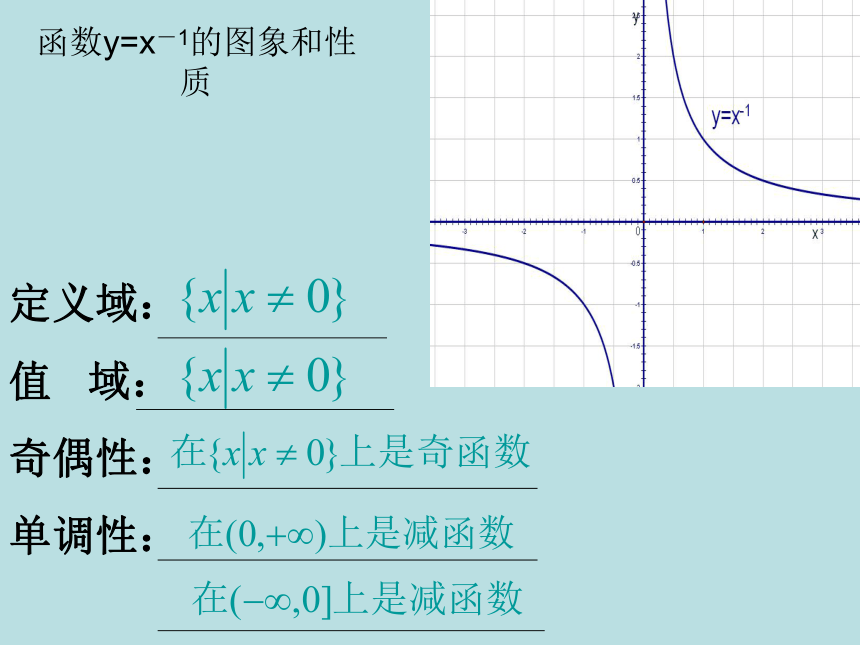
其中 a 是常数且 a ∈ R 。2。幂函数的定义域：使 x a 有意义的实数的集合。函数y=x的图象和性质函数y=x2的图象和性质函数y=x3的图象和性质函数y=x0.5的图象和性质函数y=x－1的图象和性质作出下列函数的图象:(1,1)(2,4)(-2,4)(-1,1)(-1,-1)从图象能得出他们的性质吗?几个幂函数的性质:X y110y=x2y=x3y=x1/2X y110y=x-1y=x-2y=x-1/2a > 0a < 0 （1）图象都过（0，0）点和
（1，1）点；
（2）在第一象限内，函数值
随x 的增大而增大，即
在（0，+∞)上是增函
数。 （1）图象都过（1，1）点；
（2）在第一象限内，函数值随
x 的增大而减小，即在
（0，+∞）上是减函数。
（3）在第一象限，图象向上与
y 轴无限接近，向右与 x
轴无限接近。幂函数在第一象限的性质小结当 n > 0Oyxy=x n>10 图象向右与 x 轴无限地接近 。一般幂函数的性质:★所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1).
★如果α>0,则幂函数的图象过点(0,0),(1,1)并在(0,+∞)上为增函数.
★幂函数的定义域、奇偶性，单调性，
因函数式中α的不同而各异.一般幂函数的性质:★如果α<0,则幂函数的图象过点(1,1),并在(0,+∞)上为减函数.
★当α为奇数时,幂函数为奇函数,
★当α为偶数时,幂函数为偶函数.
例1、 比较大小：
（1）1.53/5 1.73/5 （2）0.71.5 0.61.5
（3）2.2-2/3 1.8-2/3 （4）0.15-1.2 0.17-1.2
<<>>例2、求下列函数的定义域：
（1）y = (2x+5)1/2 （2）y = (x-3)-1/5(1)解:y =
x≥-5/2函数y = (2x+5)1/2 的
定义域为[ -5/2，+∞) .解：y = 解不等式 x – 3 ≠0得X ≠ 3 函数y=(x-3)-1/5的定
义域为(-∞,3)∪(3,+∞).解不等式2x+5≥0 得 练习： 1。判断下列函数哪些是幂函数：
（1）y =5x （2）y =2x （3）y =x0.3
（4）y =x+1 （5）y =1 / x4 （6）y =xxx
√Xxx√ 2。用不等式填空：
（1）0.24/5___0.54/5 （2）0.0125___0.0115
（3）7-5/2___6.9-5/2 （4）1.01-0.5___1.001-0.5

（5） ____ （6） ___ <><<>> 3。求下列幂函数的定义域：
（1）y=x0 （2）y=x3/2


（3）y=x-2/3 （4）y=x0.2x≠0x≠0
x≥0R ===x1/5= 4。若(a+1)-1<(3-2a)-1，试求a的取值范围。方法技巧:分子有理化休息一下