3.1.2《指数函数》

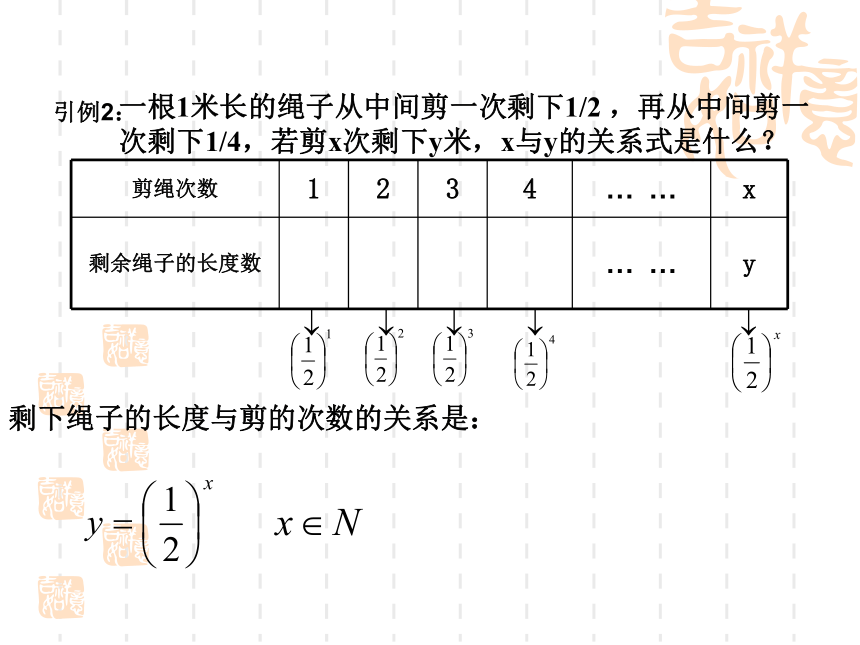
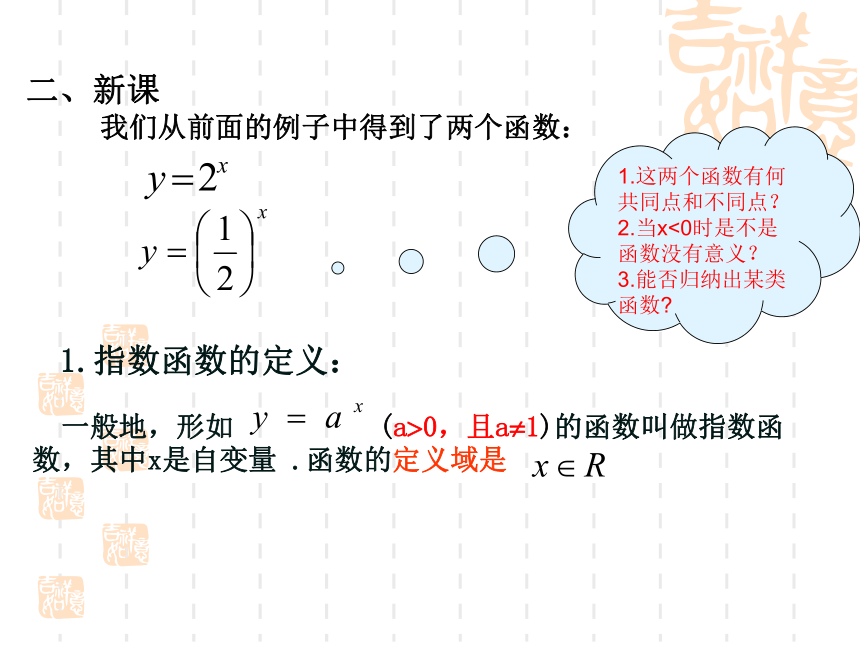
课件14张PPT。3.1.2 指数函数一、复习引入：引例1：某种细胞分裂时，由1个变成了2个，2个分裂成4个，……1个这样的细胞分裂x次后，得到的细胞个数y与x的函数关系式是什么？第 x 次细胞个数y关于分裂次数x的表达式为：……剩下绳子的长度与剪的次数的关系是： 二、新课我们从前面的例子中得到了两个函数：1.这两个函数有何共同点和不同点？ 2.当x<0时是不是函数没有意义？
3.能否归纳出某类函数?
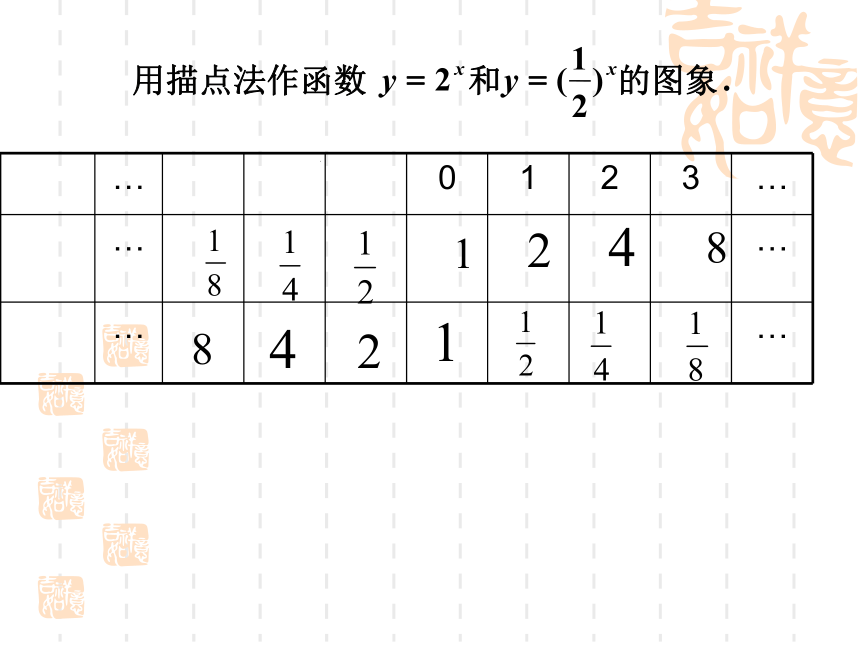
1.指数函数的定义：1.指数函数定义思考：为何规定a?0，且a?1?★而当a=1时，函数值y恒等于1，没有研究的价值.★指数函数解析式y=ax的系数是1练习1：指出下列函数哪些是指数函数xy0123-3-2-1y=2x2481y=2-x作图62.指数函数的图象和性质图象全在x轴上方，与x轴无限接近。值域为(0,+?).当x>0时,y>1;当x<0时,00时, 01.自左向右图象逐渐上升自左向右图象逐渐下降图象过定点（0，1）图象过定点（0，1）5.图象无对称性(既不关于原点对称,也不关于y轴对称)非奇非偶函数.以a的取值来分以y=1来分图像位置决定X=０,y=１例.比较下列各题中两个值的大小： (1)1.7a ,1.7a+1 (2)0.8– 0.1 ,0.8–0.2 解：(1)考察指数函数y=1.7x ∵a1 ,所以指数函数在R上是增函数.练习2.求下列函数的定义域、值域：解：(1)要时函数有意义，须x≠0 ∴函数的定义域为{x|x ? 0}, 值域为{y|y>0 ,且y?1}.练习3：.(0,1].)34()41()2(;)3()3()1(.4,)21(.3.,)12()(.2.1,,.)10(,.1655321311---=+=>∈≠>=∈比较下列各题中两个值的大小：值域是的定义域是函数是的取值范围则是减函数若函数时当这时为增函数且函数时当xxxyaaxfyxaaaya(1,+?)(0, +?)[1, +?)><三、小结： 1.学习指数函数 y=ax 时，应当画图象，抓特征，说性质，做到数形结合. 3.比较两实数大小时，若底数相同可以运用指数函数的增减性来比较，若底数不同可以通过中间值 1 来比较大小. 2.函数y=ax与y=a-x的图象关于y轴对称.
(a＞0且a≠1) 4.指数函数形如y=ax(a＞0且a≠1)，定义域为R，值域为(0,+∞) 作业 P93 习题3—1A 2，4
练习：P92 练习A，B