3.2.1《对数的概念》
图片预览






文档简介
课件15张PPT。对数的概念新课引入上节课我们学习指数函数,研究细胞分裂时,曾经归纳出,第x次分裂后,细胞的个数为y=2x;给定分裂的次数x,我们可以求出细胞个数y。有时我们会遇到这样的问题:
已知一个细胞分裂x次后细胞的个数是1024,问这个细胞分裂了几次?
即:2x=1024,则x=?所以须要创立新的符号,能在已知底数和幂的值时,表示出该指数的表达式.这就是我们本节课将要学习的对数及对数符号. 又看如下问题: 现今我国总产值每年比上年约平均增长8%,问经过几年,总产值是今年的2倍?
设今年总产值为a亿元,经过x年,总产值是今年的2倍,则可列式: a(1+8%)x=2a, 即得 1.08x=2 此式的x如何解出(表达出)呢?新课引入形成概念 一般地,如果a(a>0,a≠1)的 b 次幂等于N, 即ab=N, 那么数b叫做以a为底 N的对数,
记作: logaN=b
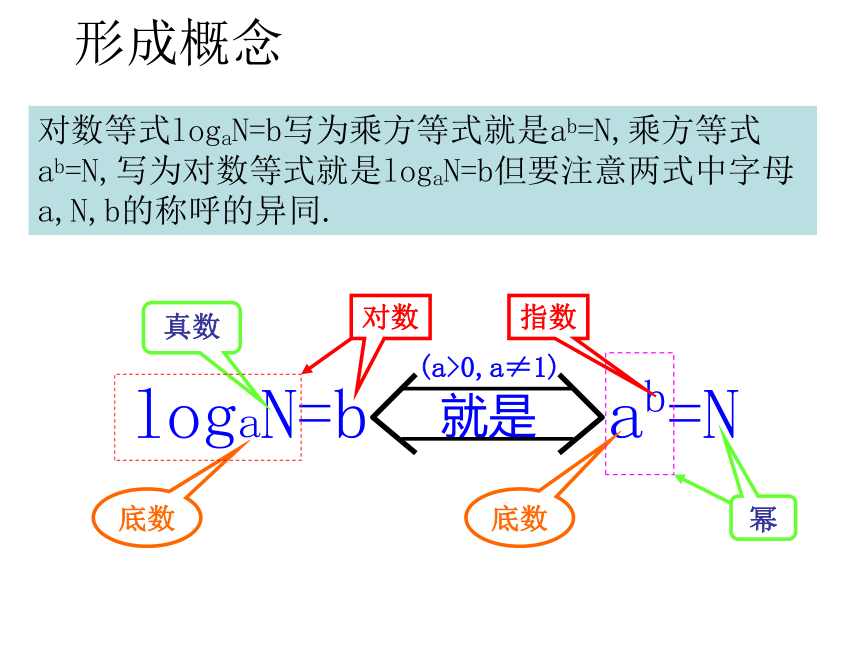
(式中的a叫做对数的底数,N叫做真数.)(对数式 “logaN” 表示的意思就是:一个乘方的底数是a,乘方的结果是N时所“对应的那个指数”)书写格式:对数等式logaN=b写为乘方等式就是ab=N,乘方等式ab=N,写为对数等式就是logaN=b但要注意两式中字母a,N,b的称呼的异同. logaN=b 就是 ab=N底数底数真数幂对数指数(a>0,a≠1)形成概念概念深化?由对数式定义: logaN=b ? ab=N (a>0,a≠1) 可知,不论b是什么实数,总有ab>0,即式ab=N中的幂N永远是正数,也即式logaN中的真数N永远是正数. 因此负数和零没有对数. 例如:
式log20, log3(-3),以及log05, log-23, log12等都无意义.?有了对数知识,前面提出的“已知底数和幂的值,如何用(含有底数和幂的)式子去表达出与其对应的指数”之问题就迎刃而解了. 例如,因为42=16,所以底数为4,幂为16,对数(对应的指数)是2,就可写为 log416=2★从事例:20=1,写为对数就是log21=0;(0.3)0=1就是log0.31=0;
100=1就是log101=0. 猜想应有公式:证明:设loga1=x 由对数的定义就有ax=1,又1=a0(a>0,a≠1)
∴ ax=a0 ∴一定有x=0.即得 loga1=0. ★从事例:21=2,写为对数就是log22=1;(0.3)1=0.3就是log0.30.3=1;
101=10就是log1010=1. 猜想应有公式:概念深化证明:设logaa=x 由对数的定义就有ax=a,又a=a1(a>0,a≠1)
∴ ax=a1 ∴一定有x=1.即得 logaa=1. X思考:此指数式(指数是logaN)写为对数式就是 logaX=logaN ,
令 logaX=logaN=b,则有ab=X又有ab=N ∴X=N.∴得公式解:?概念深化对数恒等式 例1 将下列指数式写成对数式:
(1)54=625log5625=4.解:解:(3)3a=27解:log327=a.解:例2 将下列对数式写成指数式:解:(2)log2128=7解:27=128.(3)lg0.01=-2解:10-2=0.01.例3. (1)求 log279的值解:设log279=b, (2)已知 2logx8=4,求x 的值.解:由2logx8=4, 先化简得 logx8=2,再化为 33b=32,∴3b=2.由对数式的定义则有 x2=8.由对数式的定义则有27b=9,解:∵只有C中两式的底数不同(一为3,另一为9)∴C不正确,选C. 3.如果N=a2(a>0,且a≠1),则有( )
(A).log2N=a (B).log2a=N
(C).logNa=2 (D).logaN=2 解.根据对数的定义, N=a2中的指数2叫做以
a为底N的对数,记作 logaN=2. ∴应选 D.课堂练习=2 =-4
=2 =-2
=4 =-4=1 =0
=2 =2
=3 =5回顾反思本节课我们学了哪些内容? 你有什么收获?我们应注意什么?好好学习 天天向上
已知一个细胞分裂x次后细胞的个数是1024,问这个细胞分裂了几次?
即:2x=1024,则x=?所以须要创立新的符号,能在已知底数和幂的值时,表示出该指数的表达式.这就是我们本节课将要学习的对数及对数符号. 又看如下问题: 现今我国总产值每年比上年约平均增长8%,问经过几年,总产值是今年的2倍?
设今年总产值为a亿元,经过x年,总产值是今年的2倍,则可列式: a(1+8%)x=2a, 即得 1.08x=2 此式的x如何解出(表达出)呢?新课引入形成概念 一般地,如果a(a>0,a≠1)的 b 次幂等于N, 即ab=N, 那么数b叫做以a为底 N的对数,
记作: logaN=b
(式中的a叫做对数的底数,N叫做真数.)(对数式 “logaN” 表示的意思就是:一个乘方的底数是a,乘方的结果是N时所“对应的那个指数”)书写格式:对数等式logaN=b写为乘方等式就是ab=N,乘方等式ab=N,写为对数等式就是logaN=b但要注意两式中字母a,N,b的称呼的异同. logaN=b 就是 ab=N底数底数真数幂对数指数(a>0,a≠1)形成概念概念深化?由对数式定义: logaN=b ? ab=N (a>0,a≠1) 可知,不论b是什么实数,总有ab>0,即式ab=N中的幂N永远是正数,也即式logaN中的真数N永远是正数. 因此负数和零没有对数. 例如:
式log20, log3(-3),以及log05, log-23, log12等都无意义.?有了对数知识,前面提出的“已知底数和幂的值,如何用(含有底数和幂的)式子去表达出与其对应的指数”之问题就迎刃而解了. 例如,因为42=16,所以底数为4,幂为16,对数(对应的指数)是2,就可写为 log416=2★从事例:20=1,写为对数就是log21=0;(0.3)0=1就是log0.31=0;
100=1就是log101=0. 猜想应有公式:证明:设loga1=x 由对数的定义就有ax=1,又1=a0(a>0,a≠1)
∴ ax=a0 ∴一定有x=0.即得 loga1=0. ★从事例:21=2,写为对数就是log22=1;(0.3)1=0.3就是log0.30.3=1;
101=10就是log1010=1. 猜想应有公式:概念深化证明:设logaa=x 由对数的定义就有ax=a,又a=a1(a>0,a≠1)
∴ ax=a1 ∴一定有x=1.即得 logaa=1. X思考:此指数式(指数是logaN)写为对数式就是 logaX=logaN ,
令 logaX=logaN=b,则有ab=X又有ab=N ∴X=N.∴得公式解:?概念深化对数恒等式 例1 将下列指数式写成对数式:
(1)54=625log5625=4.解:解:(3)3a=27解:log327=a.解:例2 将下列对数式写成指数式:解:(2)log2128=7解:27=128.(3)lg0.01=-2解:10-2=0.01.例3. (1)求 log279的值解:设log279=b, (2)已知 2logx8=4,求x 的值.解:由2logx8=4, 先化简得 logx8=2,再化为 33b=32,∴3b=2.由对数式的定义则有 x2=8.由对数式的定义则有27b=9,解:∵只有C中两式的底数不同(一为3,另一为9)∴C不正确,选C. 3.如果N=a2(a>0,且a≠1),则有( )
(A).log2N=a (B).log2a=N
(C).logNa=2 (D).logaN=2 解.根据对数的定义, N=a2中的指数2叫做以
a为底N的对数,记作 logaN=2. ∴应选 D.课堂练习=2 =-4
=2 =-2
=4 =-4=1 =0
=2 =2
=3 =5回顾反思本节课我们学了哪些内容? 你有什么收获?我们应注意什么?好好学习 天天向上
