《等腰三角形性质》教案设计
文档属性
| 名称 | 《等腰三角形性质》教案设计 |  | |
| 格式 | rar | ||
| 文件大小 | 134.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-24 22:46:00 | ||
图片预览



文档简介
人民教育出版社八年级数学(上册) 《等腰三角形性质》教案设计
人民教育出版社八年级数学(上册) 《等腰三角形性质》教案设计
12.3.1 等腰三角形的性质
授课题目:等腰三角形的性质 课型:新授课
授课对象:八年级学生 授课学时:1课时 (45分钟)
参考教材:义务教育课程标准实验教材书数学八年级上册(人民教育出版社)
一、教学目标
1、知识目标:掌握等腰三角形的“等边对等角”以及“三线合一”的性质并熟练运用其进行有关的论证和计算。
2、能力目标: 通过学生实践、观察、猜想、探究、证明等腰三角形的性质,发展学生合情推理能力和演绎推理能力。
3、情感目标:经历“几何画板”探索数学规律,激发学生的好奇心和求知欲,同时培养学生勇于探索的精神。
二、教学重点
等腰三角形的性质及其证明。
三、教学难点
等腰三角形性质的证明。
四、教学辅助
多媒体、可折叠的等腰三角形纸板。
五、教学方法
根据本节内容特点,体现“学为主体,教为主导”的现代教学思想,拟采用启发探究法和学生的动手实践、观察、猜想、探究和证明相结合的教学方法。
六、教学过程:
教学环节 创设情境孕育新知 师生互动探求新知 指导应用动手实践 快速抢答运用新知 归纳小结反馈回授 知识延伸分层作业
教学时间 5分钟 19分钟 9分钟 6分钟 3分钟 3分钟
教学环节 教学内容
一创设情境孕育新知 创设情境(4分钟)用“几何画板” 演绎等腰三角形“三线合一”的性质,如图,在中,是高,是角平分线,是中线,请用鼠标拖动的任意顶点。观察:当边、、的大小满足( )条件时,高,角平分线,中线三线重合。 (由一个学生控制鼠标,其余同学可以出谋划策,共同探索出条件=。)教学意图创设情境,激起兴趣;为证明等腰三角形两底角相等而作辅助线埋下伏笔,从而突破作辅助线的难关;学生寻找什么三角形有“三线合一”的性质,学会了动手、动眼、动脑三维一体,多种刺激,调动了学生学习的积极性,培养学生勇于探索,团结协作的精神。构造悬念,启发导入(1分钟)为什么只有在等腰三角形中才有三线重合的结论?带着这个问题,我们今天来共同探讨等腰三角形的性质。
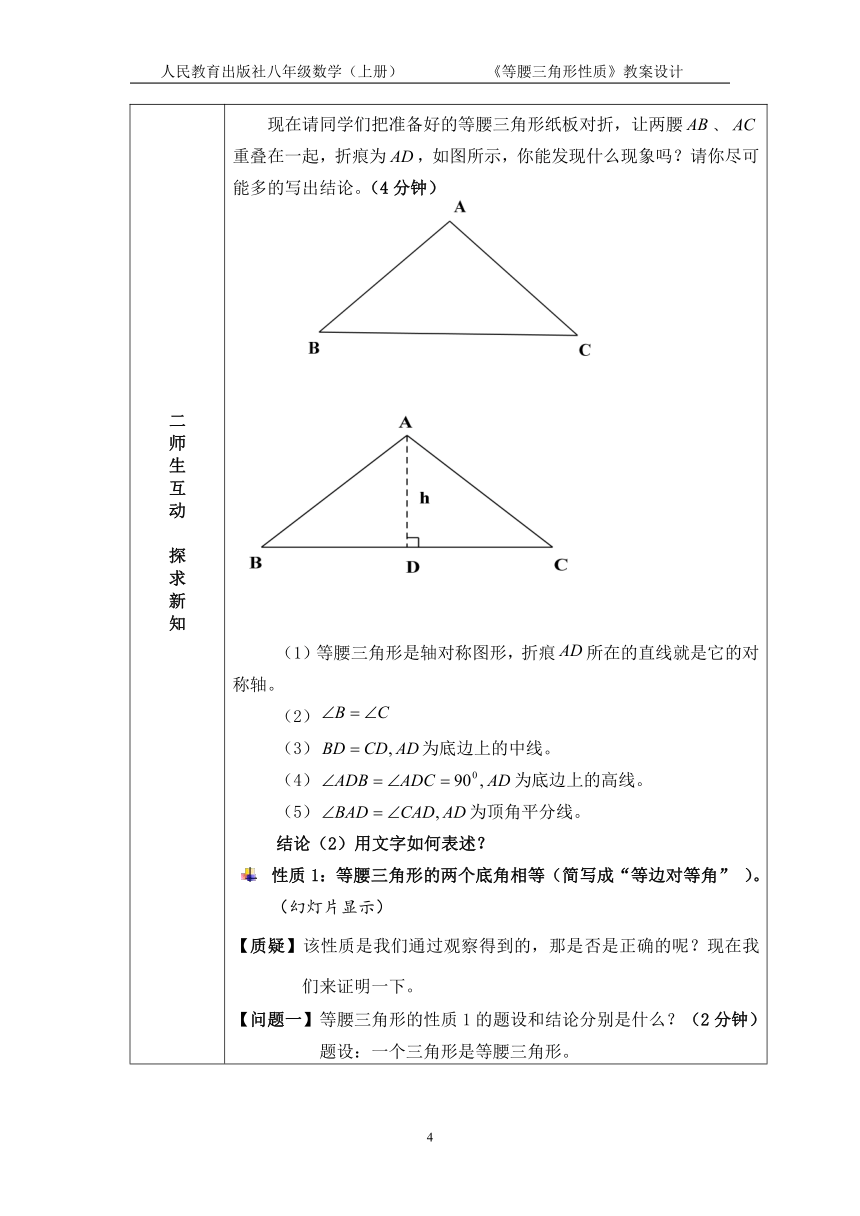
二师生互动探求新知二师生互动探求新知 现在请同学们把准备好的等腰三角形纸板对折,让两腰、重叠在一起,折痕为,如图所示,你能发现什么现象吗?请你尽可能多的写出结论。(4分钟) (1)等腰三角形是轴对称图形,折痕所在的直线就是它的对称轴。(2)(3)为底边上的中线。(4)为底边上的高线。(5)为顶角平分线。结论(2)用文字如何表述?性质1:等腰三角形的两个底角相等(简写成“等边对等角” )。(幻灯片显示)【质疑】该性质是我们通过观察得到的,那是否是正确的呢?现在我们来证明一下。【问题一】等腰三角形的性质1的题设和结论分别是什么?(2分钟)题设:一个三角形是等腰三角形。结论:两个底角相等。【问题二】如图,根据题设和结论,我们该怎样把该性质的文字语言用几何语言表达?(2分钟)已知条件:在中,= 求证:
【问题三】我们该怎么证明?(8分钟)<导析> 1.如何证明两个角相等? 2.如何构造两个全等三角形?作辅助线的方法:1.作的角平分线2.作的中线3.作底边的高分小组分别用三种方法证明。证明:(用幻灯片显示三种证法)教师对学生所做的三种证法进行评价,并强调证明的基本步骤和书写格式。(同时用幻灯片显示三种证法)
【问题四】同学们从刚才的实践(3)(4)(5)和证明过程中有何发现?(3分钟)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互 相重合(简写成“三线合一” )。(幻灯片显示) 教学意图:引导学生全面观察、联想,突破引辅助线的难关,并向学生渗透转化的数学思想引出学生探究心理;学生通过自主探索获取知识,充分发挥学生的学习主动性,体现在课堂上学生是主体,教师是参与者,合作者。
三指导应用动手实践 例1:P50,如图(见课本),在中,=,点在上,且。求各角的度数。(4分钟)解法:(见课本)例2:P57 第8题:某地震过后,河沿村中学的同学用下面的方法检测教室的房梁是否水平:在等腰直角三角尺斜边中点栓一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点,同学们确信房梁是水平的。他们的判断对吗?为什么?(5分钟)【导析】根据等腰三角形的性质2教学意图:运用所学的知识和方法寻求解决实际问题的策略,以及体验数学来源于生活又服务于生活。
四快速抢答运用新知 巩固练习:(6分钟)1.如果等腰三角形的一个底角,顶角( )。2.如果等腰三角形的一个角,其余两角( )。3.如果等腰三角形的一个角,其余两角( )。教师评析三道题目,并强调:1.等腰三角形内角和为2个底角+1个顶角=。2.顶角。3. 底角。教学意图:使学生熟悉分类讨论的数学思想。
五归纳小结反馈回授 在学生自行小结的基础上进行:(幻灯片显示)(3分钟)(一)等腰三角形性质1:等腰三角线的两底角相等。(在证明过程中,常利用性质1)(二)等腰三角形性质2:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。(三)求有关等腰三角形的问题,作顶角平分线、底边中线、底边的高是常用的辅助线。(四)求解等腰三角形的顶角、底角的度数。(五)知识的发现过程:观察—实验—猜想—证明—发现。教学意图:通过让学生自己小结本节内容,可以相互取长补短,达到对知识理解得系统和全面的效果,也更体现了学生是主体的地位。
六知识延伸分层作业 知识延伸:(2分钟)我们已经学习了等腰三角形的性质1、2,那我们又怎么知道一个三角形就是等腰三角形呢?(幻灯片显示)如图,位于海上两处的两艘救生船接到处遇险船只的报警,当时测得。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?【提示】在一般的三角形中,如果有两个角相等,那么他们所对的边有什么关系?(课下讨论)分层作业:(1分钟)基础练习:P56 3、7选作练习:P58 13
七、板书设计
12.3.1等腰三角形的性质一、性质1:等边对等角证明:(过程) 二、性质2:三线合一 例1:……例2:……
PAGE
8
人民教育出版社八年级数学(上册) 《等腰三角形性质》教案设计
12.3.1 等腰三角形的性质
授课题目:等腰三角形的性质 课型:新授课
授课对象:八年级学生 授课学时:1课时 (45分钟)
参考教材:义务教育课程标准实验教材书数学八年级上册(人民教育出版社)
一、教学目标
1、知识目标:掌握等腰三角形的“等边对等角”以及“三线合一”的性质并熟练运用其进行有关的论证和计算。
2、能力目标: 通过学生实践、观察、猜想、探究、证明等腰三角形的性质,发展学生合情推理能力和演绎推理能力。
3、情感目标:经历“几何画板”探索数学规律,激发学生的好奇心和求知欲,同时培养学生勇于探索的精神。
二、教学重点
等腰三角形的性质及其证明。
三、教学难点
等腰三角形性质的证明。
四、教学辅助
多媒体、可折叠的等腰三角形纸板。
五、教学方法
根据本节内容特点,体现“学为主体,教为主导”的现代教学思想,拟采用启发探究法和学生的动手实践、观察、猜想、探究和证明相结合的教学方法。
六、教学过程:
教学环节 创设情境孕育新知 师生互动探求新知 指导应用动手实践 快速抢答运用新知 归纳小结反馈回授 知识延伸分层作业
教学时间 5分钟 19分钟 9分钟 6分钟 3分钟 3分钟
教学环节 教学内容
一创设情境孕育新知 创设情境(4分钟)用“几何画板” 演绎等腰三角形“三线合一”的性质,如图,在中,是高,是角平分线,是中线,请用鼠标拖动的任意顶点。观察:当边、、的大小满足( )条件时,高,角平分线,中线三线重合。 (由一个学生控制鼠标,其余同学可以出谋划策,共同探索出条件=。)教学意图创设情境,激起兴趣;为证明等腰三角形两底角相等而作辅助线埋下伏笔,从而突破作辅助线的难关;学生寻找什么三角形有“三线合一”的性质,学会了动手、动眼、动脑三维一体,多种刺激,调动了学生学习的积极性,培养学生勇于探索,团结协作的精神。构造悬念,启发导入(1分钟)为什么只有在等腰三角形中才有三线重合的结论?带着这个问题,我们今天来共同探讨等腰三角形的性质。
二师生互动探求新知二师生互动探求新知 现在请同学们把准备好的等腰三角形纸板对折,让两腰、重叠在一起,折痕为,如图所示,你能发现什么现象吗?请你尽可能多的写出结论。(4分钟) (1)等腰三角形是轴对称图形,折痕所在的直线就是它的对称轴。(2)(3)为底边上的中线。(4)为底边上的高线。(5)为顶角平分线。结论(2)用文字如何表述?性质1:等腰三角形的两个底角相等(简写成“等边对等角” )。(幻灯片显示)【质疑】该性质是我们通过观察得到的,那是否是正确的呢?现在我们来证明一下。【问题一】等腰三角形的性质1的题设和结论分别是什么?(2分钟)题设:一个三角形是等腰三角形。结论:两个底角相等。【问题二】如图,根据题设和结论,我们该怎样把该性质的文字语言用几何语言表达?(2分钟)已知条件:在中,= 求证:
【问题三】我们该怎么证明?(8分钟)<导析> 1.如何证明两个角相等? 2.如何构造两个全等三角形?作辅助线的方法:1.作的角平分线2.作的中线3.作底边的高分小组分别用三种方法证明。证明:(用幻灯片显示三种证法)教师对学生所做的三种证法进行评价,并强调证明的基本步骤和书写格式。(同时用幻灯片显示三种证法)
【问题四】同学们从刚才的实践(3)(4)(5)和证明过程中有何发现?(3分钟)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互 相重合(简写成“三线合一” )。(幻灯片显示) 教学意图:引导学生全面观察、联想,突破引辅助线的难关,并向学生渗透转化的数学思想引出学生探究心理;学生通过自主探索获取知识,充分发挥学生的学习主动性,体现在课堂上学生是主体,教师是参与者,合作者。
三指导应用动手实践 例1:P50,如图(见课本),在中,=,点在上,且。求各角的度数。(4分钟)解法:(见课本)例2:P57 第8题:某地震过后,河沿村中学的同学用下面的方法检测教室的房梁是否水平:在等腰直角三角尺斜边中点栓一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点,同学们确信房梁是水平的。他们的判断对吗?为什么?(5分钟)【导析】根据等腰三角形的性质2教学意图:运用所学的知识和方法寻求解决实际问题的策略,以及体验数学来源于生活又服务于生活。
四快速抢答运用新知 巩固练习:(6分钟)1.如果等腰三角形的一个底角,顶角( )。2.如果等腰三角形的一个角,其余两角( )。3.如果等腰三角形的一个角,其余两角( )。教师评析三道题目,并强调:1.等腰三角形内角和为2个底角+1个顶角=。2.顶角。3. 底角。教学意图:使学生熟悉分类讨论的数学思想。
五归纳小结反馈回授 在学生自行小结的基础上进行:(幻灯片显示)(3分钟)(一)等腰三角形性质1:等腰三角线的两底角相等。(在证明过程中,常利用性质1)(二)等腰三角形性质2:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。(三)求有关等腰三角形的问题,作顶角平分线、底边中线、底边的高是常用的辅助线。(四)求解等腰三角形的顶角、底角的度数。(五)知识的发现过程:观察—实验—猜想—证明—发现。教学意图:通过让学生自己小结本节内容,可以相互取长补短,达到对知识理解得系统和全面的效果,也更体现了学生是主体的地位。
六知识延伸分层作业 知识延伸:(2分钟)我们已经学习了等腰三角形的性质1、2,那我们又怎么知道一个三角形就是等腰三角形呢?(幻灯片显示)如图,位于海上两处的两艘救生船接到处遇险船只的报警,当时测得。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?【提示】在一般的三角形中,如果有两个角相等,那么他们所对的边有什么关系?(课下讨论)分层作业:(1分钟)基础练习:P56 3、7选作练习:P58 13
七、板书设计
12.3.1等腰三角形的性质一、性质1:等边对等角证明:(过程) 二、性质2:三线合一 例1:……例2:……
PAGE
8
