函数的基本性质复习
图片预览






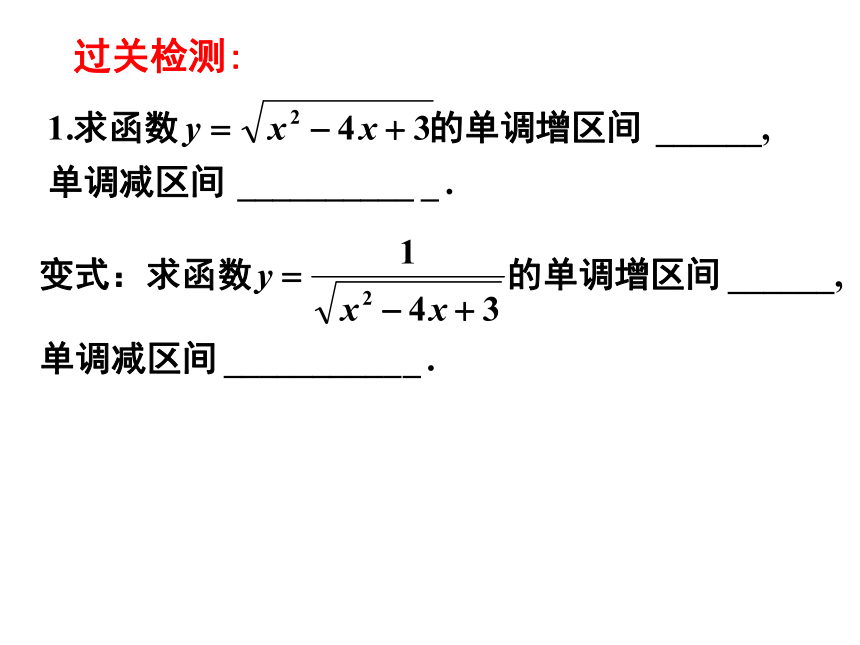
文档简介
课件17张PPT。函数的基本性质复习课知识回顾函数的单调性: 函数的奇偶性:定义:函数的最值: 最大值、最小值增函数、减函数奇函数、偶函数 1、如果对于定义域I内某个区间D上的任意两个
自变量的值x1,x2,当x1那么就说函数f (x)在区间D上是增函数。这一
区间叫做f(x)的单调增区间 2、如果对于定义域I内某个区间D上的任意两个
自变量的值x1,x2,当x1f(x2),
那么就说函数f (x)在区间D上是减函数。这一
区间叫做f(x)的单调减区间函数单调性定义法①任取②作差③变形④判号⑤下结论 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最大值 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≥M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最小值 函数最值函数奇偶性 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)= -f(x),那么f(x)就叫做奇函数. 用定义判断函数奇偶性的步骤:(1)、先求定义域,看是否关于原点对称;(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.复合函数单调性 设y=f(u), u=g(x), 则y关于x的函数 y=f[g(x)] 叫做函数
f与g的复合函数,u叫中间量. 结论:
已知函数y=f[g(x)]. 若u=g(x)在区间(a,b)上是增函数,
其值域为(c,d),又函数y=f(u)在区间(c,d)上是增函数,
那么,原复合函数y=f[g(x)]在区间(a,b)上是增函数 .规律:
“同增异减”过关检测: 函数的单调性和奇偶性(综合)思考:(1)若奇函数f(x)在(0,+∞)上是增函数,那么f(x)在(-∞,0)上是增函数还是减函数?(2)若f(x)是偶函数又有怎样的情形呢?奇函数在关于原点对称的区间上单调性一致. 偶函数在关于原点对称的区间上单调性相反。一.判断函数的单调性及最值二.判断函数的奇偶性例2.已知函数f(x)是奇函数,当x >0时,f(x)=x(1-x),求f(x)在R上的表达式.点评:关键是求出x<0时的表达式,要坚持“问啥设啥”的原则!最后结果是分段函数.三.利用函数的奇偶性求解析式2-2【例4】思考你能画出f(x)的大致图像吗 ?答案:四.函数的性质的综合应用(0,1)课堂练习:1.若奇函数f(x)当x<0时f(x)=x2-5,则f(6)= .2.若奇函数f(x)在[-7,-3]上是增函数且最小值为5,
那么f(x)在[3,7]上是 函数且最 值为 。3.若定义域为(-∞,0)∪(0,+∞)的奇函数f(x)的一部分图象(如图),则不等式f(x)>0的解集为 .练习:1.设f(x)是定义域为R的奇函数,且当x >0时,
f(x)= -2x2+3x+1,试求函数f(x)的解析式,四、方法总结—对本章的题型及解决方法系统归纳(1)利用单调性可求函数的最值,证明单调性要利用定义。(2)证明奇偶性只能依据定义,利用奇偶性可画函数的图象。题型归类(1)判断函数的单调性及最值(2)判断函数的奇偶性(3)函数的单调性和奇偶性的综合应用
自变量的值x1,x2,当x1
区间叫做f(x)的单调增区间 2、如果对于定义域I内某个区间D上的任意两个
自变量的值x1,x2,当x1
那么就说函数f (x)在区间D上是减函数。这一
区间叫做f(x)的单调减区间函数单调性定义法①任取②作差③变形④判号⑤下结论 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最大值 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≥M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最小值 函数最值函数奇偶性 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)= -f(x),那么f(x)就叫做奇函数. 用定义判断函数奇偶性的步骤:(1)、先求定义域,看是否关于原点对称;(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.复合函数单调性 设y=f(u), u=g(x), 则y关于x的函数 y=f[g(x)] 叫做函数
f与g的复合函数,u叫中间量. 结论:
已知函数y=f[g(x)]. 若u=g(x)在区间(a,b)上是增函数,
其值域为(c,d),又函数y=f(u)在区间(c,d)上是增函数,
那么,原复合函数y=f[g(x)]在区间(a,b)上是增函数 .规律:
“同增异减”过关检测: 函数的单调性和奇偶性(综合)思考:(1)若奇函数f(x)在(0,+∞)上是增函数,那么f(x)在(-∞,0)上是增函数还是减函数?(2)若f(x)是偶函数又有怎样的情形呢?奇函数在关于原点对称的区间上单调性一致. 偶函数在关于原点对称的区间上单调性相反。一.判断函数的单调性及最值二.判断函数的奇偶性例2.已知函数f(x)是奇函数,当x >0时,f(x)=x(1-x),求f(x)在R上的表达式.点评:关键是求出x<0时的表达式,要坚持“问啥设啥”的原则!最后结果是分段函数.三.利用函数的奇偶性求解析式2-2【例4】思考你能画出f(x)的大致图像吗 ?答案:四.函数的性质的综合应用(0,1)课堂练习:1.若奇函数f(x)当x<0时f(x)=x2-5,则f(6)= .2.若奇函数f(x)在[-7,-3]上是增函数且最小值为5,
那么f(x)在[3,7]上是 函数且最 值为 。3.若定义域为(-∞,0)∪(0,+∞)的奇函数f(x)的一部分图象(如图),则不等式f(x)>0的解集为 .练习:1.设f(x)是定义域为R的奇函数,且当x >0时,
f(x)= -2x2+3x+1,试求函数f(x)的解析式,四、方法总结—对本章的题型及解决方法系统归纳(1)利用单调性可求函数的最值,证明单调性要利用定义。(2)证明奇偶性只能依据定义,利用奇偶性可画函数的图象。题型归类(1)判断函数的单调性及最值(2)判断函数的奇偶性(3)函数的单调性和奇偶性的综合应用
