4.1 正弦和余弦（1）

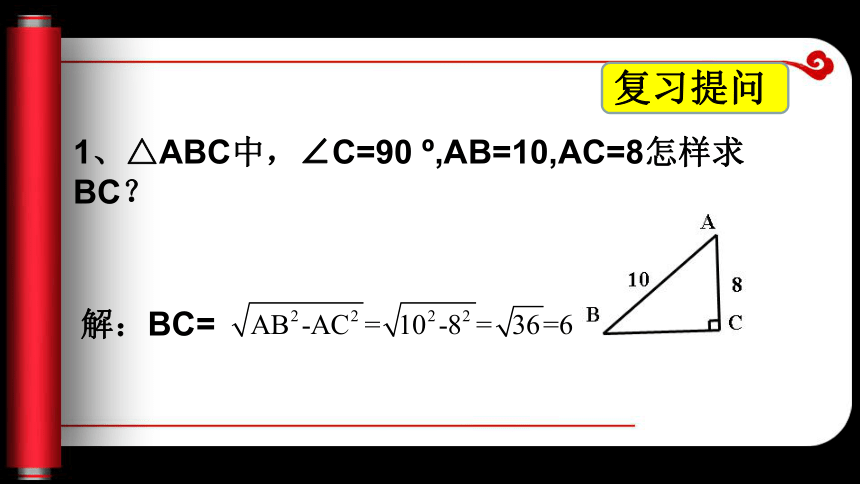
课件20张PPT。4.1 正弦和余弦湖南省新邵县酿溪中学王军旗 第1课时 正弦的概念复习提问1、△ABC中，∠C=90 o,AB=10,AC=8怎样求BC？解：BC=如图，一艘轮船从西
向东航行到B处，灯塔
A在船的正北方向，轮
船从B继续向正东方向
航行2000m到达C处，
此时灯塔A在船的北偏西65 o方向，试问：C处和灯塔A的距离AC约等于多少米？（精确到10米）
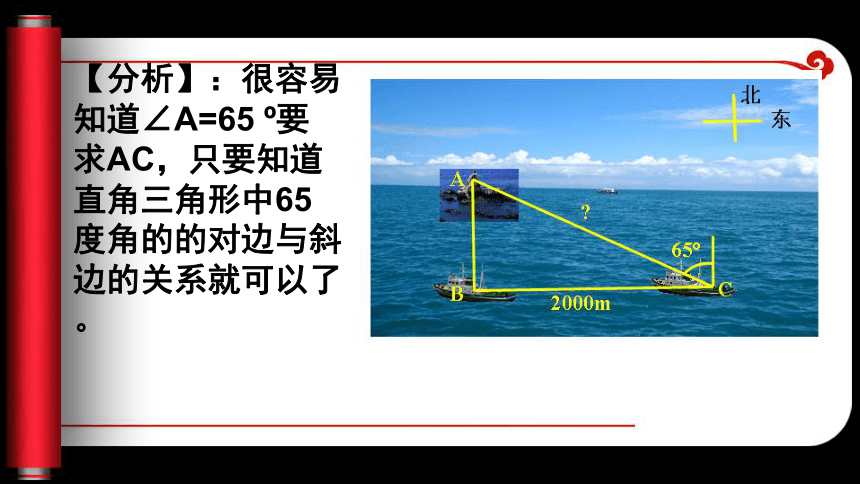
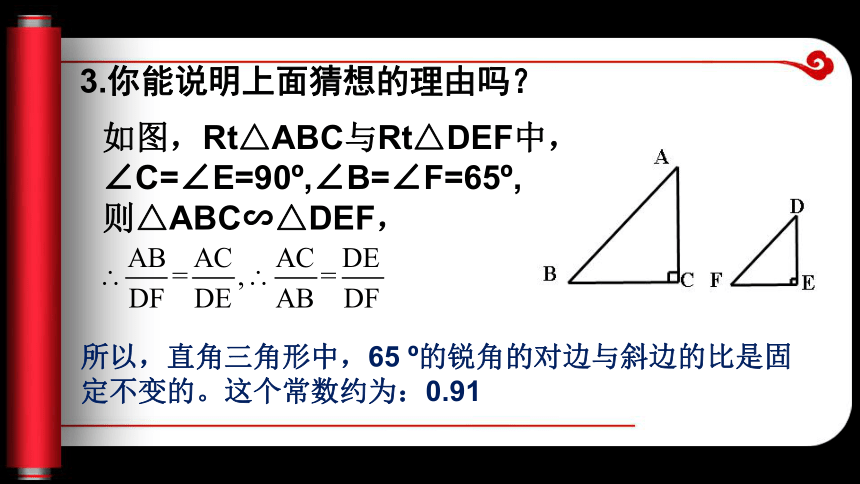
新课引言【分析】：很容易知道∠A=65 o要求AC，只要知道直角三角形中65度角的的对边与斜边的关系就可以了。做一做1.画一个直角三角形，使其中一个锐角为65 o，量出65 o锐角的对边和斜边的长，并求出65 o锐角的对边和斜边的长的比（精确到0.01）。2.与同学交流，计算出的比值是否相等？由此你有什么猜想？ 猜想：直角三角形中65o角的对边和斜边的比固定不变。几何画板3.你能说明上面猜想的理由吗？所以，直角三角形中，65 o的锐角的对边与斜边的比是固定不变的。这个常数约为：0.91如图，Rt△ABC与Rt△DEF中，∠C=∠E=90o,∠B=∠F=65o,
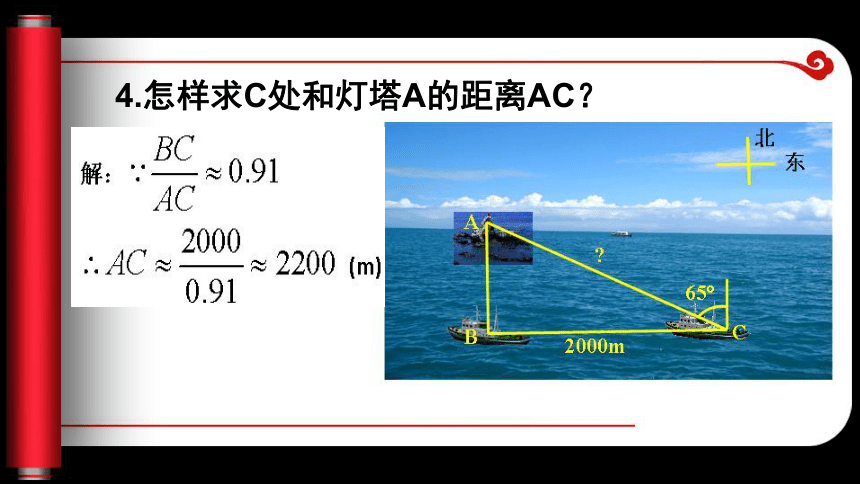
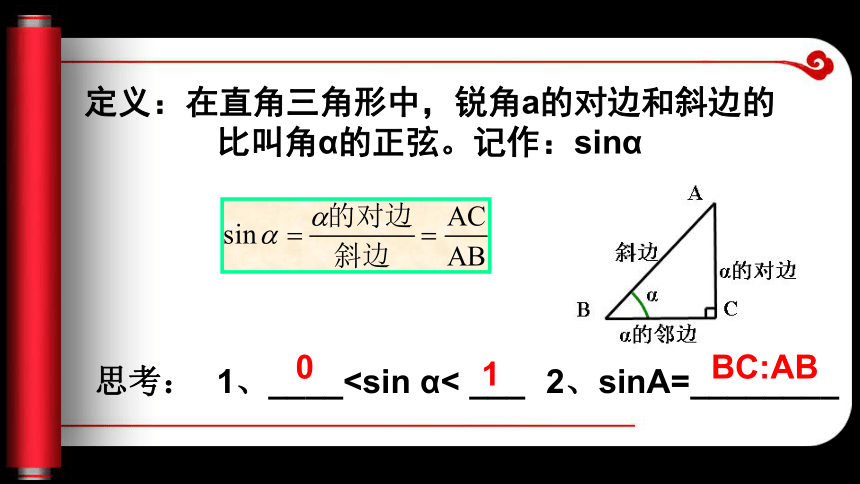
则△ABC∽△DEF，4.怎样求C处和灯塔A的距离AC？定义：在直角三角形中，锐角a的对边和斜边的比叫角α的正弦。记作：sinα思考：1、____2、角的正弦是两条线段的比值。结果没有单位。例1.在Rt△ABC中，∠C=90o,
BC=3,AB=5。(1)求sinA,(2)求sinB
.主题二、在直角三角形中求锐角的正弦解：由勾股定理，得：AC=1、在直角三角形△ ABC中，∠C=90o,BC=5,AB=13. (1)sinA=___。（2）sinB=___。变式练习C解：设BC=1,则AC=2,AB=sinA=3、如图，在Rt△ABC中，CD是斜边AB上的高，则下列线段的比不等于sinA的是（ ）A CD:AC,B BD:BC, C BC:AB, D CD:BC.D例2.如图，是亮亮沿与地面成a的斜坡向上走了90米，如果sina=1：3 ,那么他上升了多少米？主题三、在直角三角形中根据正弦求边长解：Rt △ABC中， AB=90m,
∵ sina=1：3,
∴BC:AB=1:3,
∴BC=变式练习C例3、在△ABC中，AB=AC=17,BC=16,求sinC.主题三、综合题例3、在△ABC中，AB=AC=17,BC=16,求sinC.例3、在△ABC中，AB=AC=17,BC=16,求sinC.解：作AD ⊥BC于D， ∵AB=AC=17, ∴BD=DC= ?BC=8,
AD=
∴ sinC=AD:AC=15:17
D在△ABC中，AB=AC=17,BC=16,BD⊥AC于D，求sin∠CBD.解：作AE ⊥BC于E
∵ ∠C= ∠C, ∠AEC=∠BDC=90o
∴ △BDC ∽ △AEC,
∴ ∠DBC= ∠CAE
∴sin ∠CBD=sin ∠CAE=EC:AC=8:17
变式练习E1.当一个直角三角形的锐角固定时，他的对边和斜边的比也固定。2. 定义：在直角三角形中，锐角a的对边和斜边的比叫角α的正弦。记作：sinα小结作业：P 102 ,练习题1，2 P 106 A 1