4.1 正弦和余弦（2）

课件22张PPT。4.1 正弦和余弦湖南省新邵县酿溪中学王军旗第2课时 余弦的概念复习提问什么叫角a的正弦？定义：在直角三角形中，锐角a的对边和斜边的比叫角α的正弦。记作：sinα 我们知道直角三角形中，如果一个锐角固定不变，那么这个锐角的对边和斜边的比也固定不变。那么它的邻边和斜边的比是否也固定不变呢？
这节课我来探索这个问题。
新课引言解：如图，在Rt△ABC中，
∠C=90o, ∠A=30o,则∠B=90o -∠A=60o主题讲解【例1】分别求sin30o,sin60o的值。主题一、 30o、45o、60o角的正弦值。260o设BC=1,则AB=2BC=2,AC=sinA=sin30o=sinB=sin60o=例2 求sin45o的值。如图，在Rt△ABC中，∠C=90o, ∠A=45o,则∠B=∠A=45 o,设BC=1,则AC=BC=1,AB =
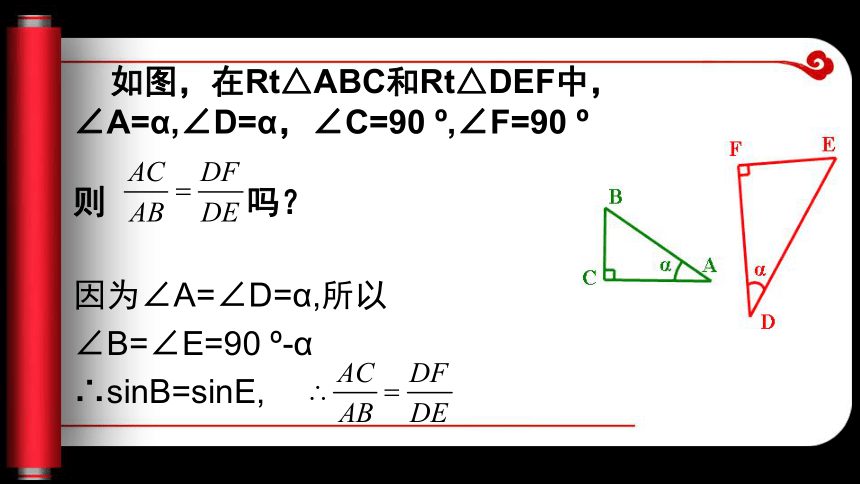
∴sinA=sin45o= “直角三角形中，如果有一个锐角a大小固定不变，这个锐角的对边与斜边的比也就固定不变”，那么当角a固定不变时，这个角的对边和斜边的比是否也固定不变呢？主题二 余弦的定义 如图，在Rt△ABC和Rt△DEF中，∠A=α,∠D=α，∠C=90 o,∠F=90 o 则 吗？因为∠A=∠D=α,所以
∠B=∠E=90 o-α
∴sinB=sinE,
定义：定义：在直角三角形中，锐角a的邻边和斜边的比叫角α的余弦。记作：cosα cosα= 思考:1、__2、cos B=
_____01如图在Rt△ABC中：
SinA=___,cosA=____,sinB=___,cosB=_____主题三、互为余角的正弦余弦的关系。你发现了什么？Rt△ABC中：
sinA=cosB, cosA=sinB用式子表示为：Rt△ABC中：
sinA=cosB,sosA=sinB
或者：sinα=cos(90 o-α),cosα=sin(90 o-α) 如果两个角互余，那么其中一个角的正弦等于另一个角的余弦，一个角的余弦等于另一个角的正弦。 比一比：看谁最先求出：30o、45o、60o角的余弦值解：sin30o=cos60o=
cos30o=sin60o=
cos45o= sin45o= 例1计算：2cos45o+sin60o解：原式=（2010辽宁丹东市）计算： ．解：原式变式练习例2 在Rt△ABC中，∠C=90o，AC=3, AB=5,求sinA,cosA的值。解：由勾股定理得：
BC=sinA=cosA=（2010湖南怀化）在Rt△ABC中，∠C=90°，sinA= ，则cosB的值等于（ ） A． B. C. D. 变式练习B例3已知：∠α+∠β=90o，若sinα=0.4321,则cosβ=___0.4321下列各式中错误的是（ ）
A sin32o=cos58o, B sin 45o=cos45o,
C sin34o=cos34o , D sin47o=cos43o变式练习C【例4】（2010 福建三明）如图，在梯形ABCD中，AD//BC，AC⊥AB，AD=CD ，
, BC=10，则AB的值是（ ）
A．9 B．8 C．6 D．3
C（2007上海）如图6，在直角坐标平面内， O为原点，点 A的坐标为(10,0) ，点B 在第一象限内 ,BO=5, ． 求：（1）点B 的坐标；（2） 的值．变式练习解：（1）如图，作BH⊥x轴 ，垂足为 ，在
Rt△OHB中，∵BO=5，
∴BH=3,OH=4 ∴点B的坐标为(4,3)．
H(2)∵OA=10,OH=4, ∴AH=6,
在Rt△AHB中，∵BH=3, ∴AB=1.余弦的概念，2特殊角的正弦和余弦值，3.锐角的正弦和余弦值的范围，4.锐角的正弦和余弦的增减性。小结作业
P 106 A 3—5 P 107 B 1---5