(华东师大版九年级上)数学:24.6.2 图形的变换与坐标 课件
文档属性
| 名称 | (华东师大版九年级上)数学:24.6.2 图形的变换与坐标 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-25 00:00:00 | ||
图片预览




文档简介
课件13张PPT。 1、方程 一次项的系数是 .
2、方程 的根是 。
3.方程 的根是_____。
4 、最简二次根式 与 是同类二次根式,则x的值是____。
4.计算: =_____。 =______。
6、相似三角形的相似比是2﹕3,则周长比是__________.
7、小红坐在第 5 排 24 号用(5,24)表示,则(6,27)表示
小红坐在第__排___号。
8、小刚画了一张脸谱上,用(1,3)表示左眼,(3,3)表示右眼(图1),
那么嘴的位置是_____.
9、点A(3,-2)关于 x 轴对称的点是_____。
10、点A(3,4)关于 y 轴对称的点是_____。
11、P(2,3)关于原点对称的点是_____。
12、 P(-2,3)到x轴的距离是_____。
13 、如图2矩形ABOC的长OB=3,宽AB=2,则点A的坐标为__。
14、如果点P(a-3,a+4)在第二象限,则a的取值范围是_____。
15、点A(a,-4)到两坐标轴的距离相等,则a=_______.-课前训练
1、 -3 2、 ± 5
3、 0, 3 4、3
5、 5, 6、2﹕3
7、 6,27 8、(2,1)
9、 (3,2) 10 、(-3,4)
11、 (-2,-3) 12、3
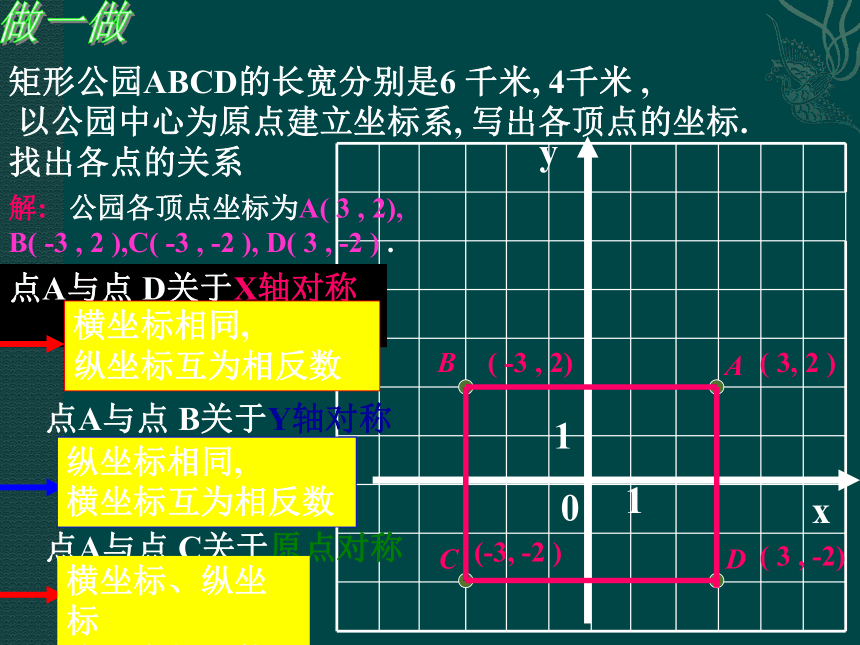
13、 (-3,2) 14 、 -415 、 ±4课前训练题答案:24.6.2图形的变换与坐标矩形公园ABCD的长宽分别是6 千米, 4千米 ,
以公园中心为原点建立坐标系, 写出各顶点的坐标.
找出各点的关系 BCDA解: 公园各顶点坐标为A( 3 , 2),
B( -3 , 2 ),C( -3 , -2 ), D( 3 , -2 ) .
做一做xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数点A与点 C关于原点对称
横坐标、纵坐标
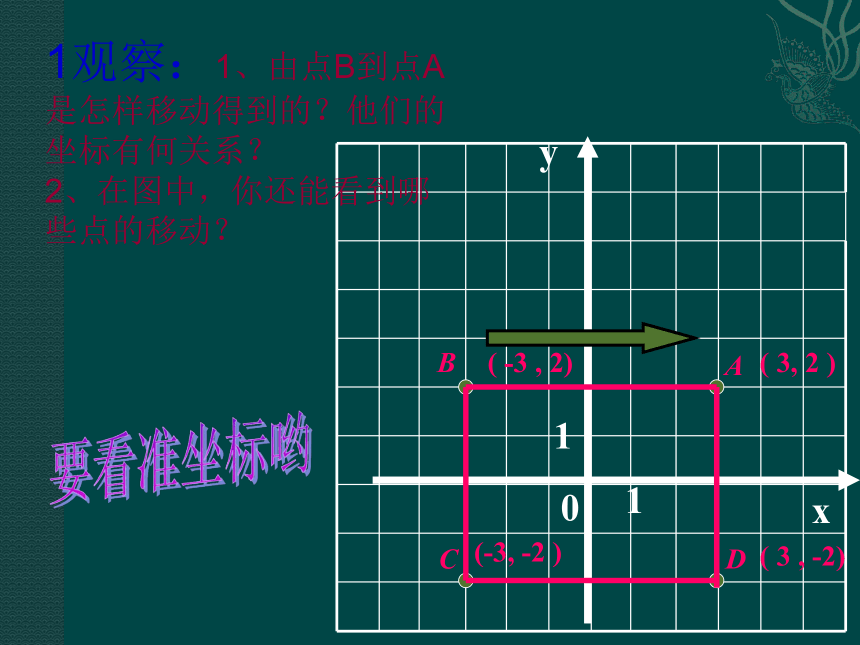
均互为相反数BCDAxy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)111观察:1、由点B到点A是怎样移动得到的?他们的坐标有何关系?
2、在图中,你还能看到哪些点的移动?要看准坐标哟2、如果是⊿AOB 向右移动3个单位长度,得到
⊿A ’O’ B ’ ,各顶点的坐标又有什么变化?你能
用自已的语言归纳这个规律吗?3、你能画图说明⊿AOB向左移动时,对应点的坐标
又有什么规律吗?O’B’YXA’规律(1)左右移动时,横坐标左减右加,纵坐标不变:4小组讨论:将⊿AOB向上或向下移动几个单位长度,
你能探索出图形上下移动的规律吗?规律:( 2)上下移动时,横坐标不变,纵坐标上加下减.YX-545、将⊿AOB沿着x轴对折,得到⊿A ’ OB,
画图并说明对应顶点有什么变化?规律:对应点关于x轴对称。即对应点的
横坐标相等、纵坐标互为相反数
YXABA’6、画出⊿ABC,A(2,1),B(4,0),C(5,2)沿y 轴
对折后的⊿A ’ B’ C ’,并观察对应顶点又有什么样的变化?
规律:对应点关于 y 轴对称。即对应点的
横坐标互为相反数、纵坐标相等
YXABCC’B’A’7、画⊿AOB关于原点对称的⊿A ’O B ’
你有什么发现?规律:对应点关于原点对称。即对应点的
横坐标和纵坐标互为相反数XYABB’A’8,能力拓展 如果将⊿AOB缩小,变成⊿COD,它
们的相似比是多少?对应点的坐标有什么变化?规律: 横坐标和纵坐标都缩小相同的倍数XYCDAB课堂小结:1、本节课我学会了……
2、我的体会是……XY4-4-2ABC24-4快乐小测:
1、画出⊿ABC向下平移4个单位后的图形
2 、画出⊿ABC关于原点对称的图形
3、以O为位似中心,将⊿ABC放大2倍
2、方程 的根是 。
3.方程 的根是_____。
4 、最简二次根式 与 是同类二次根式,则x的值是____。
4.计算: =_____。 =______。
6、相似三角形的相似比是2﹕3,则周长比是__________.
7、小红坐在第 5 排 24 号用(5,24)表示,则(6,27)表示
小红坐在第__排___号。
8、小刚画了一张脸谱上,用(1,3)表示左眼,(3,3)表示右眼(图1),
那么嘴的位置是_____.
9、点A(3,-2)关于 x 轴对称的点是_____。
10、点A(3,4)关于 y 轴对称的点是_____。
11、P(2,3)关于原点对称的点是_____。
12、 P(-2,3)到x轴的距离是_____。
13 、如图2矩形ABOC的长OB=3,宽AB=2,则点A的坐标为__。
14、如果点P(a-3,a+4)在第二象限,则a的取值范围是_____。
15、点A(a,-4)到两坐标轴的距离相等,则a=_______.-课前训练
1、 -3 2、 ± 5
3、 0, 3 4、3
5、 5, 6、2﹕3
7、 6,27 8、(2,1)
9、 (3,2) 10 、(-3,4)
11、 (-2,-3) 12、3
13、 (-3,2) 14 、 -4
以公园中心为原点建立坐标系, 写出各顶点的坐标.
找出各点的关系 BCDA解: 公园各顶点坐标为A( 3 , 2),
B( -3 , 2 ),C( -3 , -2 ), D( 3 , -2 ) .
做一做xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数点A与点 C关于原点对称
横坐标、纵坐标
均互为相反数BCDAxy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)111观察:1、由点B到点A是怎样移动得到的?他们的坐标有何关系?
2、在图中,你还能看到哪些点的移动?要看准坐标哟2、如果是⊿AOB 向右移动3个单位长度,得到
⊿A ’O’ B ’ ,各顶点的坐标又有什么变化?你能
用自已的语言归纳这个规律吗?3、你能画图说明⊿AOB向左移动时,对应点的坐标
又有什么规律吗?O’B’YXA’规律(1)左右移动时,横坐标左减右加,纵坐标不变:4小组讨论:将⊿AOB向上或向下移动几个单位长度,
你能探索出图形上下移动的规律吗?规律:( 2)上下移动时,横坐标不变,纵坐标上加下减.YX-545、将⊿AOB沿着x轴对折,得到⊿A ’ OB,
画图并说明对应顶点有什么变化?规律:对应点关于x轴对称。即对应点的
横坐标相等、纵坐标互为相反数
YXABA’6、画出⊿ABC,A(2,1),B(4,0),C(5,2)沿y 轴
对折后的⊿A ’ B’ C ’,并观察对应顶点又有什么样的变化?
规律:对应点关于 y 轴对称。即对应点的
横坐标互为相反数、纵坐标相等
YXABCC’B’A’7、画⊿AOB关于原点对称的⊿A ’O B ’
你有什么发现?规律:对应点关于原点对称。即对应点的
横坐标和纵坐标互为相反数XYABB’A’8,能力拓展 如果将⊿AOB缩小,变成⊿COD,它
们的相似比是多少?对应点的坐标有什么变化?规律: 横坐标和纵坐标都缩小相同的倍数XYCDAB课堂小结:1、本节课我学会了……
2、我的体会是……XY4-4-2ABC24-4快乐小测:
1、画出⊿ABC向下平移4个单位后的图形
2 、画出⊿ABC关于原点对称的图形
3、以O为位似中心,将⊿ABC放大2倍
