(华东师大版九年级上)数学:25.3解直角三角形(2)课件
文档属性
| 名称 | (华东师大版九年级上)数学:25.3解直角三角形(2)课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-25 15:37:00 | ||
图片预览




文档简介
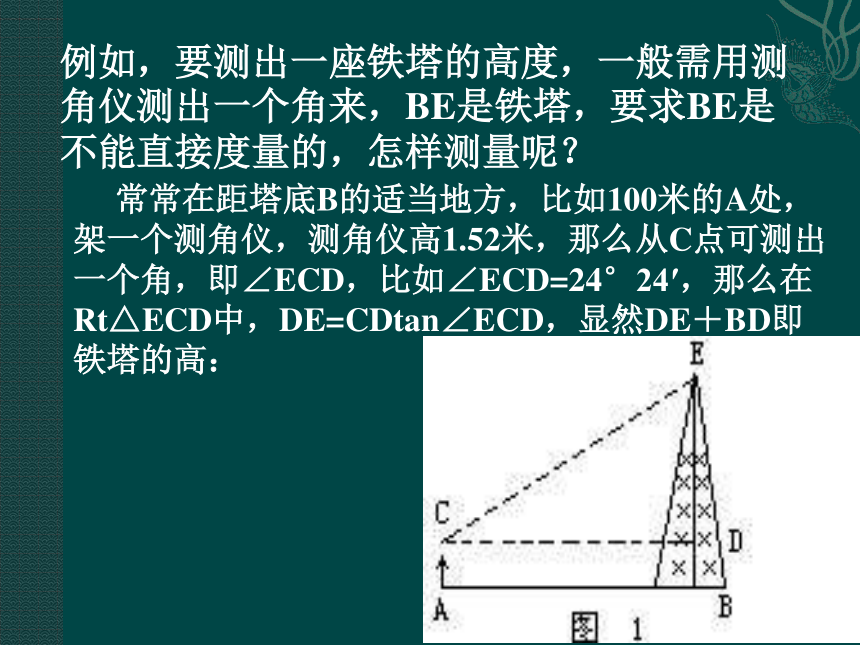
课件12张PPT。25.3.2解直角三角形ABCbc1.三边关系3. 边角关系2.锐角关系90度例如,要测出一座铁塔的高度,一般需用测角仪测出一个角来,BE是铁塔,要求BE是不能直接度量的,怎样测量呢?
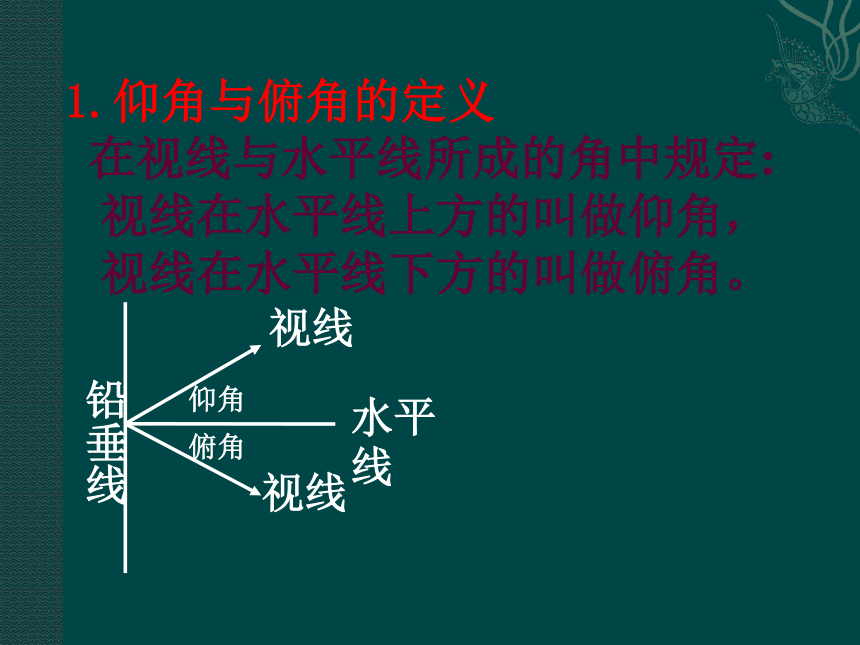
常常在距塔底B的适当地方,比如100米的A处,架一个测角仪,测角仪高1.52米,那么从C点可测出一个角,即∠ECD,比如∠ECD=24°24′,那么在Rt△ECD中,DE=CDtan∠ECD,显然DE+BD即铁塔的高: 1.仰角与俯角的定义
在视线与水平线所成的角中规定:
视线在水平线上方的叫做仰角,
视线在水平线下方的叫做俯角。铅垂线视线视线水平线仰角俯角例1 在升旗仪式上,一位同学站在离旗杆24米处,行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为30度,若两眼离地面1.5米,则旗杆的高度是否可求?若可求,求出旗杆的高,若不可求,说明理由.(精确到0.1米).A30度24米1.5米CDEBA90度解:A241.5DEBC30°答:旗杆的高为15.4米。90° 例2.河的对岸有水塔AB, 今在C处测得塔
顶A的仰角为30°,前进 20米到D处,
又测得塔顶A的仰角为60°.
求塔高AB.示意图30°60°解: 练习1.某飞机与空中A处探测到目标
C,此时飞行高度AC=1200米,
从飞机上看地平面控制点B的
俯角α=16°31′,求飞机A到
控制点B的距离。 分析:解决此类实际问题的关键是画出正
确的示意图,能说出 题目中每句话对
应图中哪个角或边,将实际问题转化
直角三角形的问题来解决。α如图:解:在RtΔABC中,
sinB=AC/AB,
∴AB=AC/sinB=AC/sin16°31′
=1200/0.2843
≈4221(米)
答:飞机A到控制点B的距离为4221米。
1200m练习2.如图8,两建筑物AB、CD的水平距离BC=32.6米,从A点测得D点的俯角α=35°12′,C点的俯角β=43°24′,求这两个建筑物的高AB和CD(精确到0.1m). 练习3 . 如图,沿AC方向开山修渠.为了加快施工进度,要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,BD=520米,∠D=50°.那么开挖点E离D多远(精确到0.1米),正好能使A,C,E成一直线?本节课我们主要研究的是关于仰角,俯角
的基本定义,及用解直角三角形的方法解
决实际问题小结:
常常在距塔底B的适当地方,比如100米的A处,架一个测角仪,测角仪高1.52米,那么从C点可测出一个角,即∠ECD,比如∠ECD=24°24′,那么在Rt△ECD中,DE=CDtan∠ECD,显然DE+BD即铁塔的高: 1.仰角与俯角的定义
在视线与水平线所成的角中规定:
视线在水平线上方的叫做仰角,
视线在水平线下方的叫做俯角。铅垂线视线视线水平线仰角俯角例1 在升旗仪式上,一位同学站在离旗杆24米处,行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为30度,若两眼离地面1.5米,则旗杆的高度是否可求?若可求,求出旗杆的高,若不可求,说明理由.(精确到0.1米).A30度24米1.5米CDEBA90度解:A241.5DEBC30°答:旗杆的高为15.4米。90° 例2.河的对岸有水塔AB, 今在C处测得塔
顶A的仰角为30°,前进 20米到D处,
又测得塔顶A的仰角为60°.
求塔高AB.示意图30°60°解: 练习1.某飞机与空中A处探测到目标
C,此时飞行高度AC=1200米,
从飞机上看地平面控制点B的
俯角α=16°31′,求飞机A到
控制点B的距离。 分析:解决此类实际问题的关键是画出正
确的示意图,能说出 题目中每句话对
应图中哪个角或边,将实际问题转化
直角三角形的问题来解决。α如图:解:在RtΔABC中,
sinB=AC/AB,
∴AB=AC/sinB=AC/sin16°31′
=1200/0.2843
≈4221(米)
答:飞机A到控制点B的距离为4221米。
1200m练习2.如图8,两建筑物AB、CD的水平距离BC=32.6米,从A点测得D点的俯角α=35°12′,C点的俯角β=43°24′,求这两个建筑物的高AB和CD(精确到0.1m). 练习3 . 如图,沿AC方向开山修渠.为了加快施工进度,要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,BD=520米,∠D=50°.那么开挖点E离D多远(精确到0.1米),正好能使A,C,E成一直线?本节课我们主要研究的是关于仰角,俯角
的基本定义,及用解直角三角形的方法解
决实际问题小结:
