(华东师大版九年级上)数学:25.3解直角三角形(3)课件
文档属性
| 名称 | (华东师大版九年级上)数学:25.3解直角三角形(3)课件 |  | |
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-25 15:37:00 | ||
图片预览






文档简介
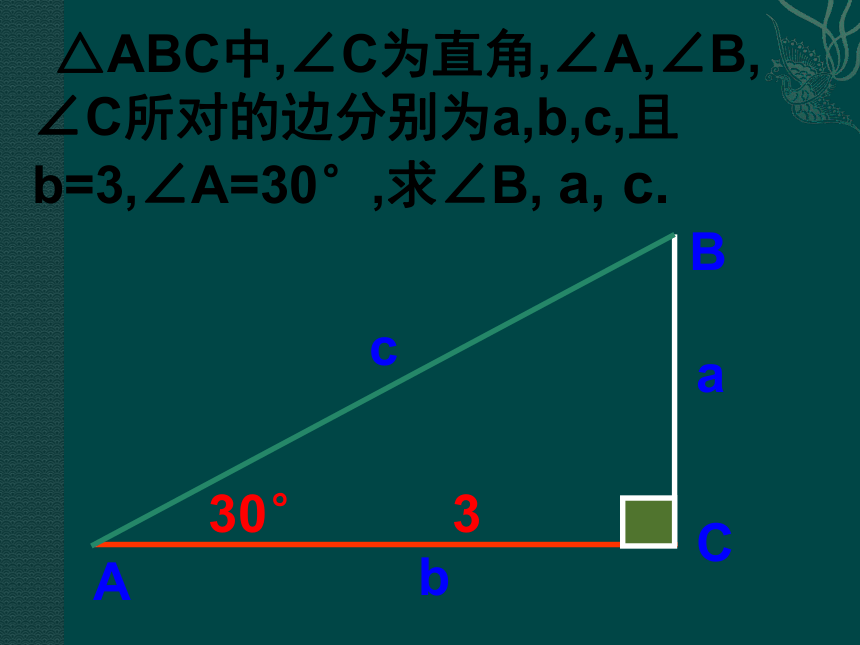
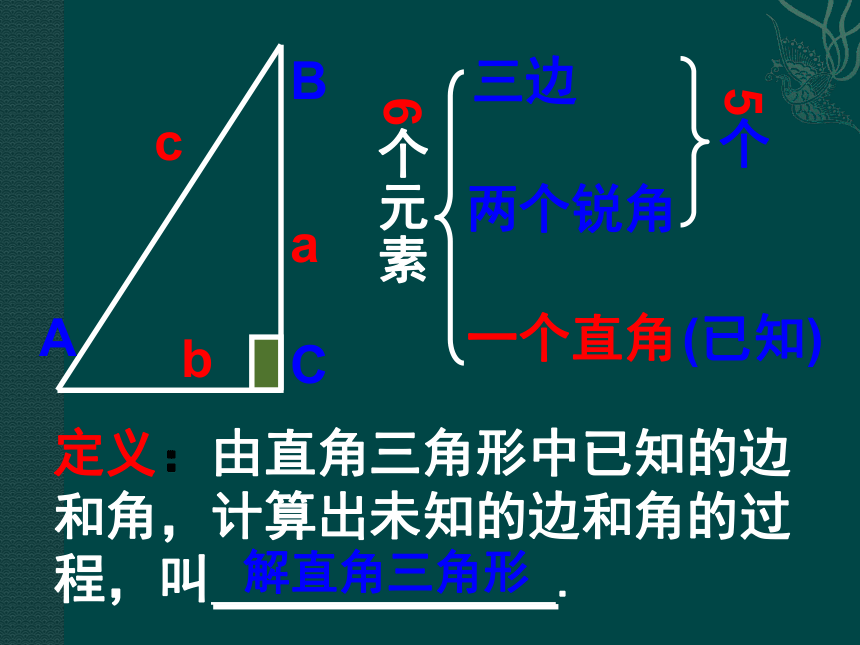
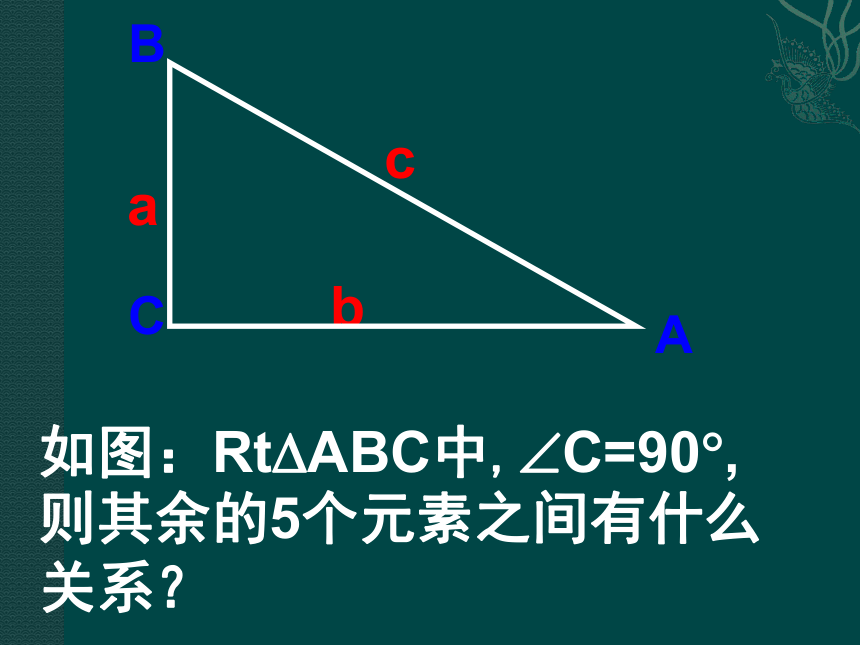
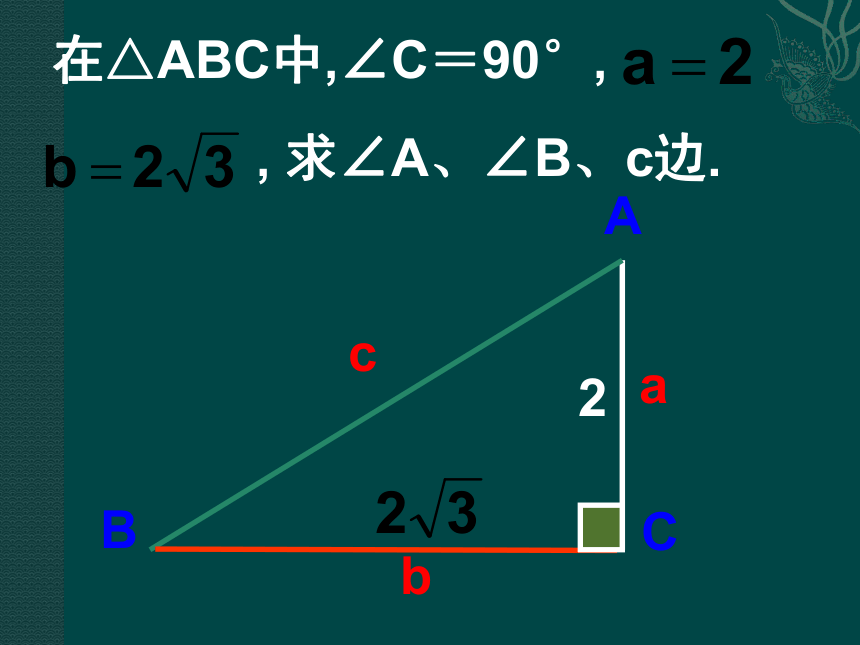
课件36张PPT。25.3.3解直角三角形 △ABC中,∠C为直角,∠A,∠B, ∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B, a, c.ABCabc330°6个元素三边两个锐角一个直角(已知)5个定义:由直角三角形中已知的边和角,计算出未知的边和角的过程,叫 . 解直角三角形ABCabc如图:Rt?ABC中,?C=90?, 则其余的5个元素之间有什么关系?bCABca???在△ABC中,∠C=90°,
, 求∠A、∠B、c边. ???1.填空:在直角三角形ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边.
??? (1)c=10,∠B=45°,则 a=? ,b= ??????S△= ?????
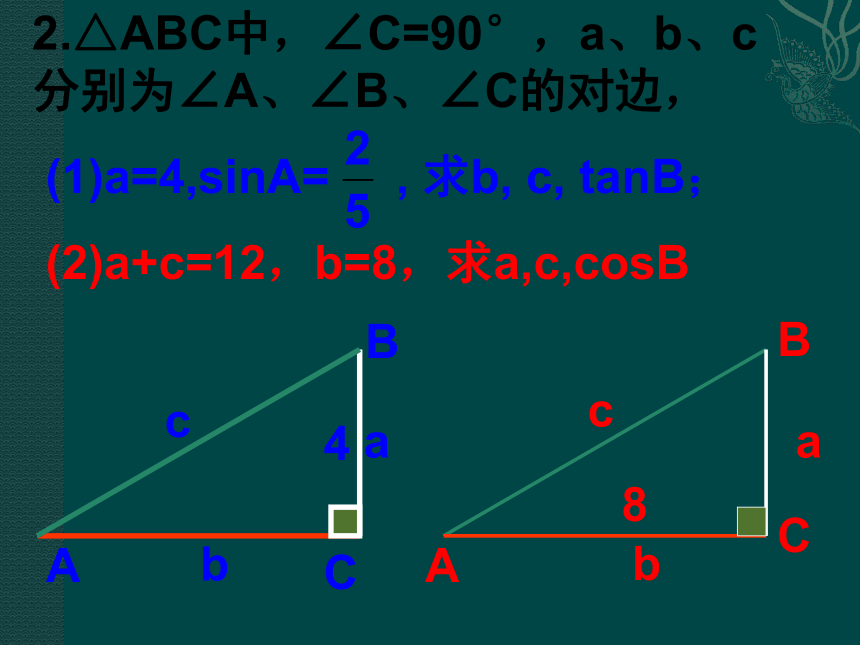
??? (2)a=10, ∠B=45°, S△= ,则b= ???? ,∠A=? ????????? 2.△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,
?(1)a=4,sinA= , 求b, c, tanB;
?(2)a+c=12,b=8,求a,c,cosBABCabcABCabc48在RtΔABC中,若∠C =900, 问题1. 在RtΔABC中,两锐角∠A, ∠B的有什么关系?答: ∠A+ ∠B= 900.问题2.在RtΔABC中,三边a、b、c的关系如何?答:a2+b2 =c2.问题3:在RtΔABC中, ∠A与边的关系是什么?答: 在解直角三角形的过程中,常会遇到近似计算,除特别说明外,边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1) 已知两条边;
(2) 已知一条边和一个锐角1.在Rt△ABC中,∠C=90°,由下列条件解直角三角形:
(1)已知a=6 ,b=6 , 则
∠B= , ∠A= ,c = ;
(2)已知c=30,∠A=60°则
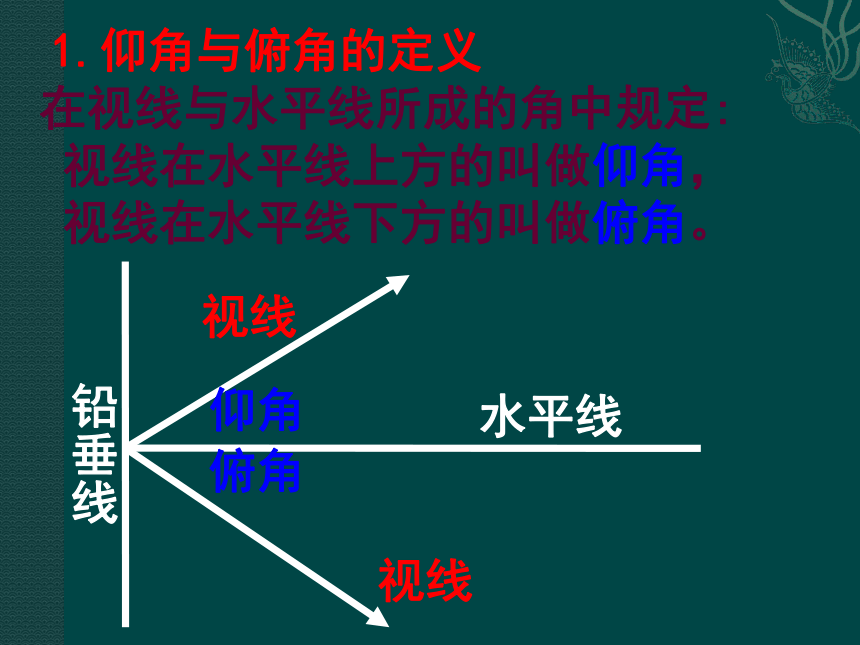
∠B= ,a = ,b = ; 1.仰角与俯角的定义
在视线与水平线所成的角中规定:
视线在水平线上方的叫做仰角,
视线在水平线下方的叫做俯角。铅垂线视线视线水平线仰角俯角1.如图,升国旗时某同学站在离旗杆24m处行注目礼,当国旗升到旗杆顶端时,这位同学的视线的仰角为30o ,若双眼离地面1.5m,则旗杆高度为多少米?30oABCDE2.在操场上一点A测得旗杆顶端的仰角为30°再向旗杆方向前进20m,又测得旗杆的顶端的仰角为45°,求旗杆的高度.(精确到1m)A20B30°DC45°坡度是指斜坡上任意一点的高度与水平距离的比值。1、什么叫坡度?2、什么叫坡角?坡角是斜坡与水平线的夹角 3、坡角和坡度什么关系? 坡角与坡度之间的关系是:
i= =tan a i=(1).一物体沿坡度为1:8的山坡向上移动 米,则物体升高了 ______米.
(2).河堤的横断面如图所示,堤高BC是5m,迎水坡AB的长是13m,那么斜坡AB的坡度是( ).
A 1:3 B 1:2.6 C 1:2.4 D 1:21C(3)如果坡角的余弦值为 ,那么坡度为( ).
A 1: B 3: C 1:3 D 3:1
B一段河坝的横断面为等腰梯形ABCD,试根据下图中的数据求出坡角a和坝底宽AD.(单位是m,结果保留根号)ABCDEF46α如图,拦水坝的横断面为梯形ABCD已知上底长CB=5m,迎水面坡度为1: 背水面坡度为1:1,坝高为4m.求(1)坡底宽AD的长.(2)迎水坡CD的长.(3)坡角α、β.如图,一段路基的横断面是梯形,高为4.2m,上底的宽是12.51m,路基的坡面与地面的倾角分别是30°和45°.求路基下底的宽.(精确到0.1m) 45°30°ABCDEF(1)、一斜坡的坡角为30度,则它的坡度为 ;
(2)、坡度通常写成1: 的形式。如果一个坡度为1 :1,则这个坡角为 ,
1: m450(3)、等腰梯形的较小底长为3,腰长为5,高为4,则另一个底长为 ,坡度为 ,
(4)、梯形的两底长分别为5和8,一腰长为4,则另一腰长X的取值范围是 。
94:31
则∠C= 。ABC如图,在△ABC中,已知AC=6,
∠C=75°,∠B=45°,求S△ABC。D求证: ABCD的面积
S=AB ·BC ·sinB(∠B为锐角)。ABCDE我军某部在一次野外训练中,有一辆坦克准备通过一座小山,且山脚和山顶的水平距离为1000m,山高为565m,如果这辆坦克能够爬300 的斜坡,试问:它能不能通过这座小山?山顶上有一旗杆,在地面上一点A处测得杆顶B的俯角α=600,杆底C的俯角β=450,已知旗杆高BC=20m,求山高CD。河的对岸有水塔AB, 今在C处测得塔顶A的仰角为30°,前进 20米到D处,又测得塔顶A的仰角为60°.求塔高AB.30°60°ABCD(1).在电线杆离地面8m高的地方向地面拉一条长10m的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
(2).海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30°处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求灯塔Q到B处的距离.(画出图形后计算,精确到0.1海里)如图,为了测量小河的宽度,在河的岸边选择B.C两点,在对岸选择一个目标点A,测∠BAC=75°, ∠ACB=45° BC=48m,求河宽.海岛A四周20海里内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?请说明理由.ABDCNN130?60?如图学校里有一块三角形形状的花圃ABC,现测∠A=30°,AC=40m , BC=25m,请你帮助计算一下这块花圃的面积?D300 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭.近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。某市计划将地处A、B两地的两所大学合并成一所综合大学,为了方便A、B两地师生的交往,学校准备在相距2千米的A、B两地之间修筑一条笔直公路(即图中的线段AB)经测量,在A地的北偏东60o方向,B地的西偏北45o方向的C处有一个半径为0.7千米的公园,问计划修筑的这条公路会不会穿过公园?为什么?D解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响(1)A城是否受到这次沙尘暴
的影响 ,为什么?ABCOCABCEFM解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?如图,一人在河对岸C处测得电视塔尖A的仰角为45o,后退100米到达D处,测得塔尖A的仰角为30o,设塔底B与C、D在同一直线上, 求电视塔的高度AB。
, 求∠A、∠B、c边. ???1.填空:在直角三角形ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边.
??? (1)c=10,∠B=45°,则 a=? ,b= ??????S△= ?????
??? (2)a=10, ∠B=45°, S△= ,则b= ???? ,∠A=? ????????? 2.△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,
?(1)a=4,sinA= , 求b, c, tanB;
?(2)a+c=12,b=8,求a,c,cosBABCabcABCabc48在RtΔABC中,若∠C =900, 问题1. 在RtΔABC中,两锐角∠A, ∠B的有什么关系?答: ∠A+ ∠B= 900.问题2.在RtΔABC中,三边a、b、c的关系如何?答:a2+b2 =c2.问题3:在RtΔABC中, ∠A与边的关系是什么?答: 在解直角三角形的过程中,常会遇到近似计算,除特别说明外,边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1) 已知两条边;
(2) 已知一条边和一个锐角1.在Rt△ABC中,∠C=90°,由下列条件解直角三角形:
(1)已知a=6 ,b=6 , 则
∠B= , ∠A= ,c = ;
(2)已知c=30,∠A=60°则
∠B= ,a = ,b = ; 1.仰角与俯角的定义
在视线与水平线所成的角中规定:
视线在水平线上方的叫做仰角,
视线在水平线下方的叫做俯角。铅垂线视线视线水平线仰角俯角1.如图,升国旗时某同学站在离旗杆24m处行注目礼,当国旗升到旗杆顶端时,这位同学的视线的仰角为30o ,若双眼离地面1.5m,则旗杆高度为多少米?30oABCDE2.在操场上一点A测得旗杆顶端的仰角为30°再向旗杆方向前进20m,又测得旗杆的顶端的仰角为45°,求旗杆的高度.(精确到1m)A20B30°DC45°坡度是指斜坡上任意一点的高度与水平距离的比值。1、什么叫坡度?2、什么叫坡角?坡角是斜坡与水平线的夹角 3、坡角和坡度什么关系? 坡角与坡度之间的关系是:
i= =tan a i=(1).一物体沿坡度为1:8的山坡向上移动 米,则物体升高了 ______米.
(2).河堤的横断面如图所示,堤高BC是5m,迎水坡AB的长是13m,那么斜坡AB的坡度是( ).
A 1:3 B 1:2.6 C 1:2.4 D 1:21C(3)如果坡角的余弦值为 ,那么坡度为( ).
A 1: B 3: C 1:3 D 3:1
B一段河坝的横断面为等腰梯形ABCD,试根据下图中的数据求出坡角a和坝底宽AD.(单位是m,结果保留根号)ABCDEF46α如图,拦水坝的横断面为梯形ABCD已知上底长CB=5m,迎水面坡度为1: 背水面坡度为1:1,坝高为4m.求(1)坡底宽AD的长.(2)迎水坡CD的长.(3)坡角α、β.如图,一段路基的横断面是梯形,高为4.2m,上底的宽是12.51m,路基的坡面与地面的倾角分别是30°和45°.求路基下底的宽.(精确到0.1m) 45°30°ABCDEF(1)、一斜坡的坡角为30度,则它的坡度为 ;
(2)、坡度通常写成1: 的形式。如果一个坡度为1 :1,则这个坡角为 ,
1: m450(3)、等腰梯形的较小底长为3,腰长为5,高为4,则另一个底长为 ,坡度为 ,
(4)、梯形的两底长分别为5和8,一腰长为4,则另一腰长X的取值范围是 。
94:31
则∠C= 。ABC如图,在△ABC中,已知AC=6,
∠C=75°,∠B=45°,求S△ABC。D求证: ABCD的面积
S=AB ·BC ·sinB(∠B为锐角)。ABCDE我军某部在一次野外训练中,有一辆坦克准备通过一座小山,且山脚和山顶的水平距离为1000m,山高为565m,如果这辆坦克能够爬300 的斜坡,试问:它能不能通过这座小山?山顶上有一旗杆,在地面上一点A处测得杆顶B的俯角α=600,杆底C的俯角β=450,已知旗杆高BC=20m,求山高CD。河的对岸有水塔AB, 今在C处测得塔顶A的仰角为30°,前进 20米到D处,又测得塔顶A的仰角为60°.求塔高AB.30°60°ABCD(1).在电线杆离地面8m高的地方向地面拉一条长10m的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
(2).海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30°处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求灯塔Q到B处的距离.(画出图形后计算,精确到0.1海里)如图,为了测量小河的宽度,在河的岸边选择B.C两点,在对岸选择一个目标点A,测∠BAC=75°, ∠ACB=45° BC=48m,求河宽.海岛A四周20海里内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?请说明理由.ABDCNN130?60?如图学校里有一块三角形形状的花圃ABC,现测∠A=30°,AC=40m , BC=25m,请你帮助计算一下这块花圃的面积?D300 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭.近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。某市计划将地处A、B两地的两所大学合并成一所综合大学,为了方便A、B两地师生的交往,学校准备在相距2千米的A、B两地之间修筑一条笔直公路(即图中的线段AB)经测量,在A地的北偏东60o方向,B地的西偏北45o方向的C处有一个半径为0.7千米的公园,问计划修筑的这条公路会不会穿过公园?为什么?D解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响(1)A城是否受到这次沙尘暴
的影响 ,为什么?ABCOCABCEFM解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?如图,一人在河对岸C处测得电视塔尖A的仰角为45o,后退100米到达D处,测得塔尖A的仰角为30o,设塔底B与C、D在同一直线上, 求电视塔的高度AB。
