线段垂直平分线
图片预览
文档简介
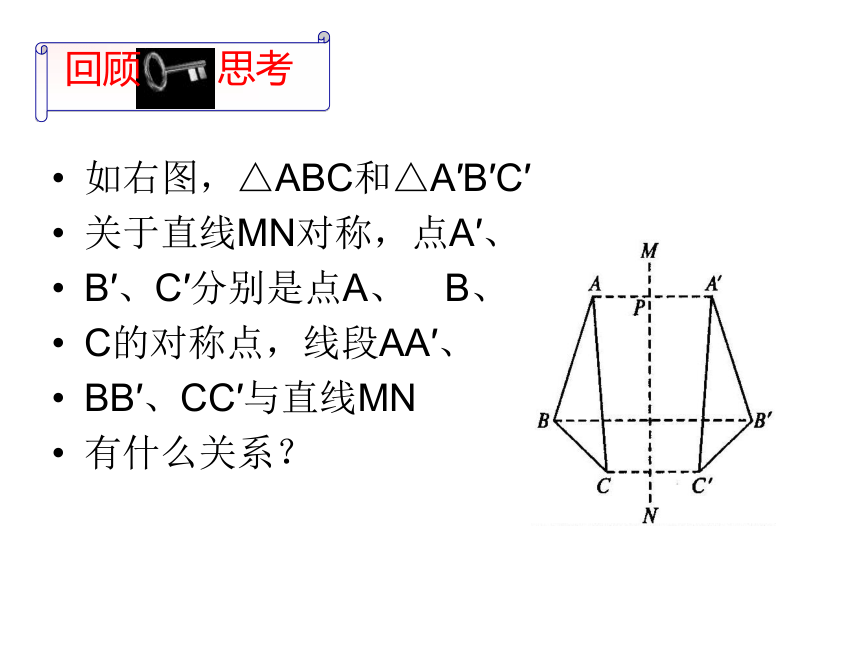
课件22张PPT。12.1.3线段垂直平分线 的性质定理及其逆定理讲课教师 李庆银ABL 在京沈高速公路L(秦皇岛段)的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?京 沈 高 速 公 路L如右图,△ABC和△A′B′C′
关于直线MN对称,点A′、
B′、C′分别是点A、B、
C的对称点,线段AA′、
BB′、CC′与直线MN
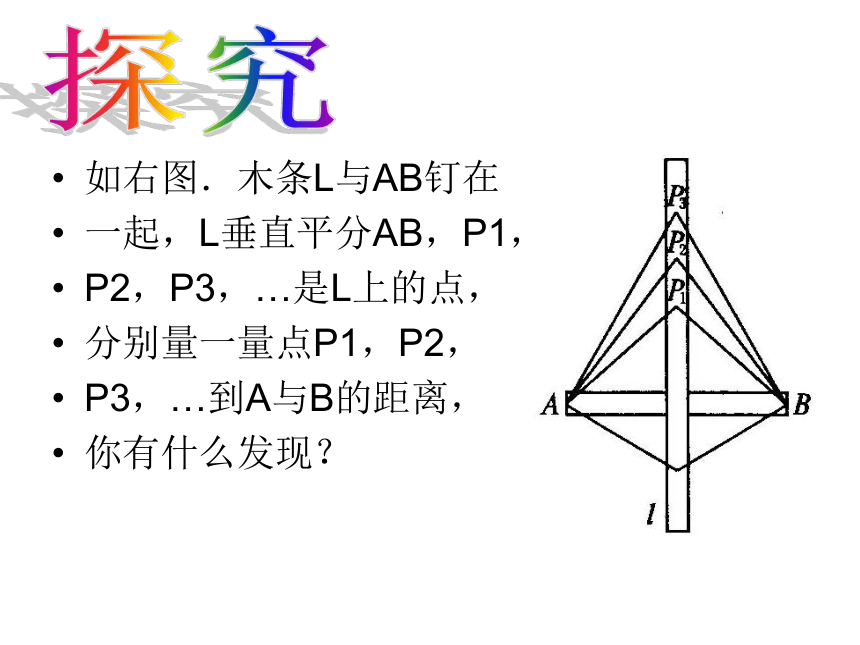
有什么关系?如右图.木条L与AB钉在
一起,L垂直平分AB,P1,
P2,P3,…是L上的点,
分别量一量点P1,P2,
P3,…到A与B的距离,
你有什么发现?探究线段的垂直平分线我们曾经利用折纸的方法得到:
线段垂直平分线上的点到这条线段两个端点距离相等.
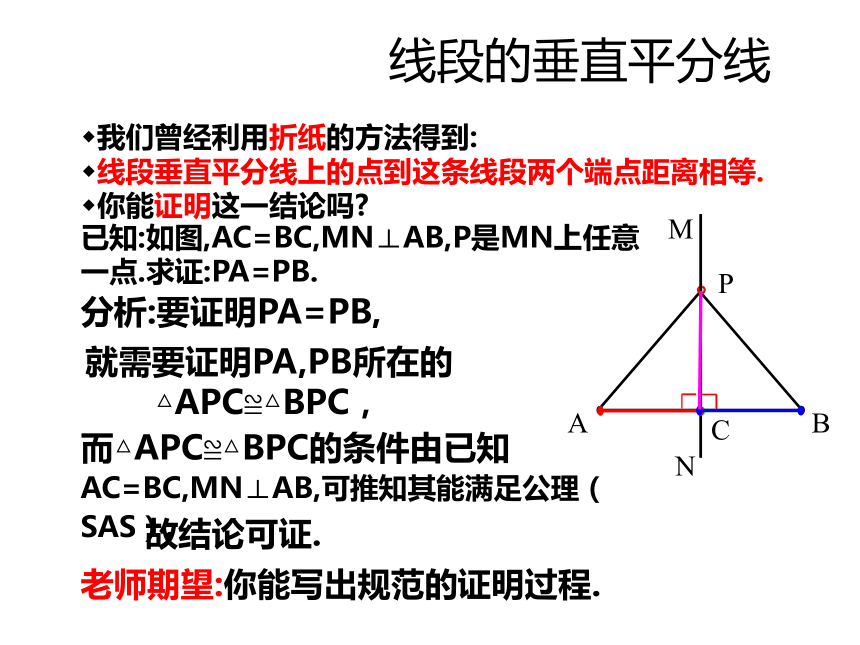
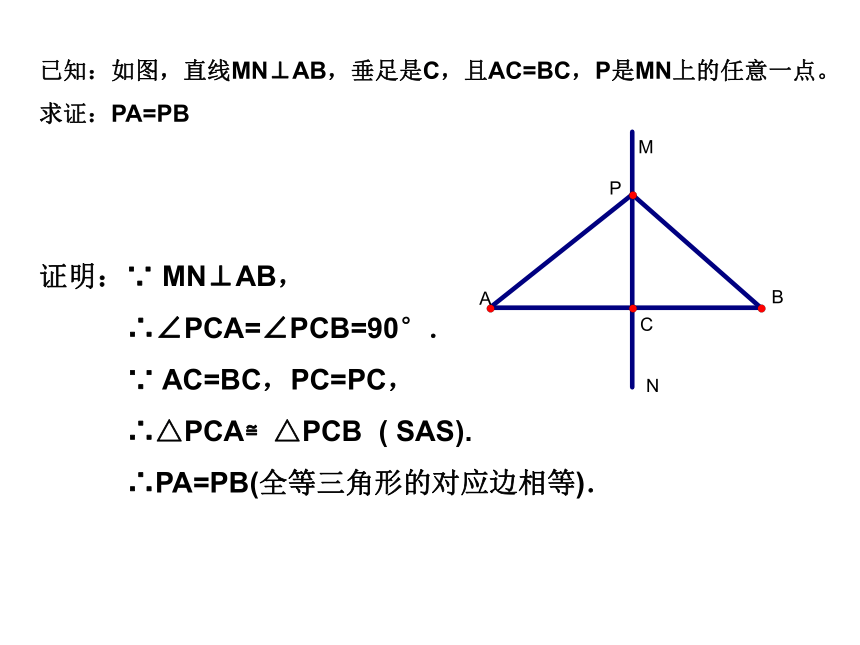
你能证明这一结论吗?已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.分析:要证明PA=PB,而△APC≌△BPC的条件由已知 故结论可证.老师期望:你能写出规范的证明过程.AC=BC,MN⊥AB,可推知其能满足公理(SAS).就需要证明PA,PB所在的△APC≌△BPC,已知:如图,直线MN⊥AB,垂足是C,且AC=BC,P是MN上的任意一点。
求证:PA=PB证明:∵ MN⊥AB,
∴∠PCA=∠PCB=90°.
∵ AC=BC,PC=PC,
∴△PCA≌△PCB ( SAS).
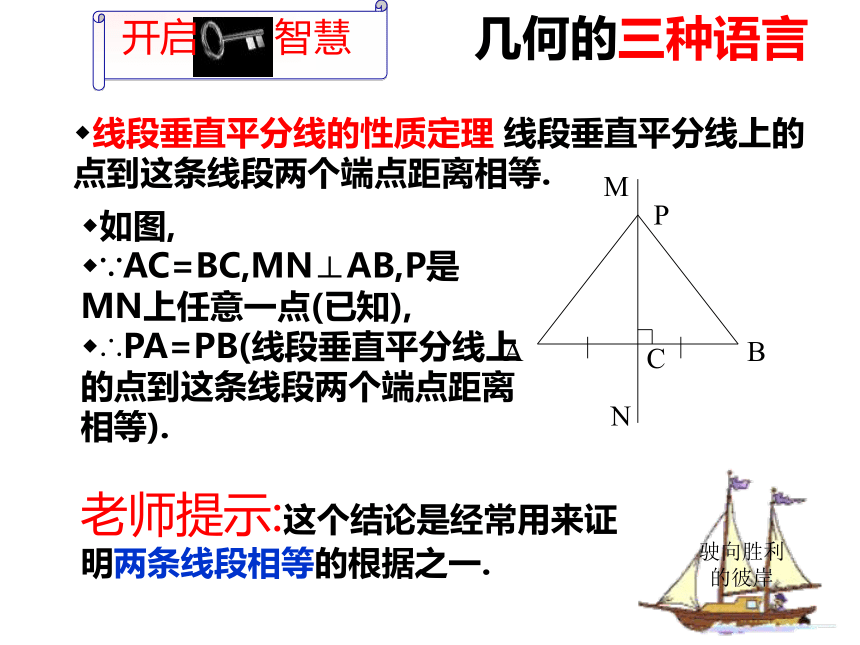
∴PA=PB(全等三角形的对应边相等).几何的三种语言线段垂直平分线的性质定理 线段垂直平分线上的点到这条线段两个端点距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.如图,
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
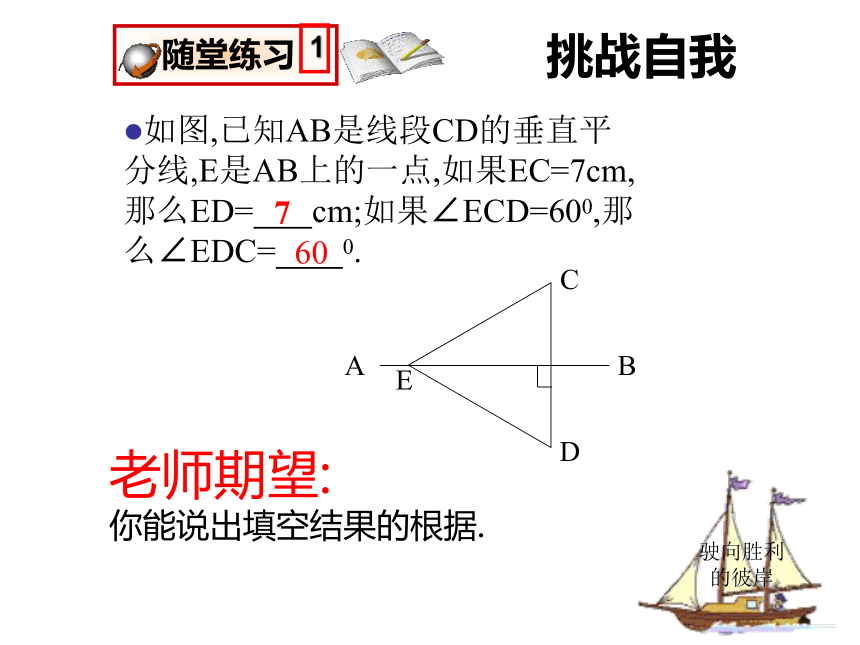
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).驶向胜利的彼岸挑战自我驶向胜利的彼岸如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.老师期望:
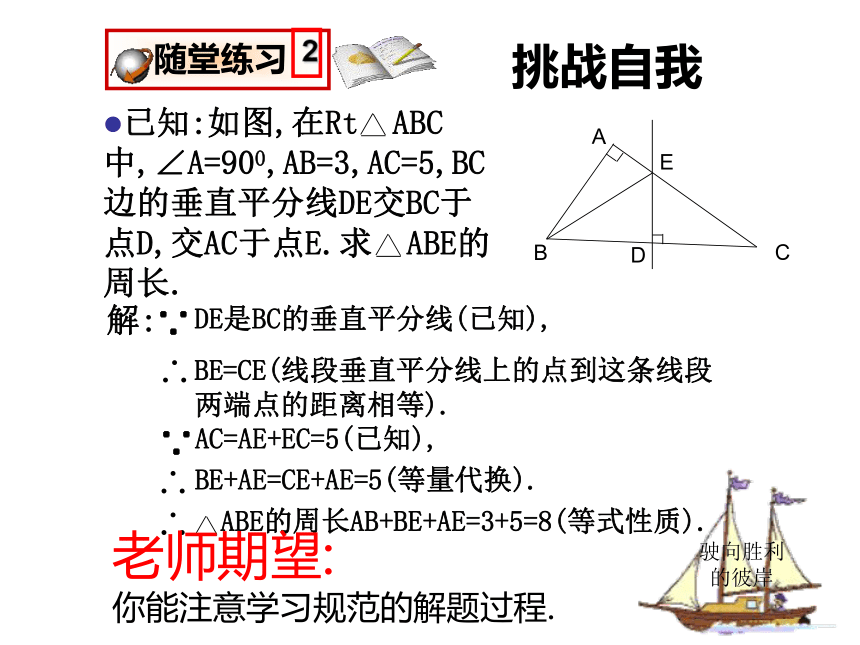
你能说出填空结果的根据.760挑战自我驶向胜利的彼岸BE+AE=CE+AE=5(等量代换).AC=AE+EC=5(已知),老师期望:
你能注意学习规范的解题过程.进步的标志′驶向胜利的彼岸你能写出“定理 线段垂直平分线上的点到这条线段两个端点距离相等”的逆命题吗?
逆命题 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.它是真命题吗?如果是.请你证明它.已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.分析:要证明点P在线段AB的垂直平分线上,可以先作出过点P的AB的垂线(或过AB中点的直线,),然后证明另一个结论正确.想一想:若作出∠P的角平分线,结论是否也可以得证?你还有其它证法吗?驶向胜利的彼岸逆定理逆定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.ABL 在京沈高速公路L(秦皇岛段)的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?京 沈 高 速 公 路分析:如图,在直线L上求作一点P,使PA=PB.老师提示 数学问题源于生活实践,反过来数学又为生活实践服务.解:连结AB,作AB的垂直平分线MN与L的交点P即为所求. 线段的垂直平分线求作一点P,使它和已△ABC的三个顶点距离相等.实际问题线段的垂直平分线的作法已知:线段AB,如图.
求作:线段AB的垂直平分线.用尺规作线段的垂直平分线.1.分别以点A和B为圆心,以大于AB/2长为半径作弧,两弧交于点C和D.2. 作直线CD.则直线CD就是线段AB的垂直平分线.请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.作法:回味无穷定理 线段垂直平分线上的点到这条线段两个端点距离相等.
如图,
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
逆定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).挑战自我驶向胜利的彼岸2.已知线段AB外两点C,D,且CA=CB,DA=DB.直线CD交AB于O,则点O是AB的____,CD是AB的________,若直线CD上还有一点E,那么EA与EB的关系是____,你的依据是______________________________.中点垂直平分线相等线段垂直平分线上的点到线段两端点的距离相等B老师期望:
你能说出选择结果的根据.老师期望:
你能说出填空结果的根据.解:AB=AC(已知),△PBQ △QCR(SAS),QP=QR(全等三角形对应边相等).点Q在PR的垂直平分线上.∠B=∠C(等边对等角).挑战自我驶向胜利的彼岸知识的升华祝你成功! 如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长。 板书设计 线段垂直平分线
1、?定理:
线段垂直平分线的性质定理;线段垂直平分线上的点到这条线段两端点的距离相等
2、逆定理:到一条线段两端点距离相等的点在这条线段的垂直平分线上结束寄语严格性之于数学家,犹如道德之于人。
证明的规范性在于:条理清晰,因果相应,言必有据。这是初学证明者谨记和遵循的原则。
关于直线MN对称,点A′、
B′、C′分别是点A、B、
C的对称点,线段AA′、
BB′、CC′与直线MN
有什么关系?如右图.木条L与AB钉在
一起,L垂直平分AB,P1,
P2,P3,…是L上的点,
分别量一量点P1,P2,
P3,…到A与B的距离,
你有什么发现?探究线段的垂直平分线我们曾经利用折纸的方法得到:
线段垂直平分线上的点到这条线段两个端点距离相等.
你能证明这一结论吗?已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.分析:要证明PA=PB,而△APC≌△BPC的条件由已知 故结论可证.老师期望:你能写出规范的证明过程.AC=BC,MN⊥AB,可推知其能满足公理(SAS).就需要证明PA,PB所在的△APC≌△BPC,已知:如图,直线MN⊥AB,垂足是C,且AC=BC,P是MN上的任意一点。
求证:PA=PB证明:∵ MN⊥AB,
∴∠PCA=∠PCB=90°.
∵ AC=BC,PC=PC,
∴△PCA≌△PCB ( SAS).
∴PA=PB(全等三角形的对应边相等).几何的三种语言线段垂直平分线的性质定理 线段垂直平分线上的点到这条线段两个端点距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.如图,
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).驶向胜利的彼岸挑战自我驶向胜利的彼岸如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.老师期望:
你能说出填空结果的根据.760挑战自我驶向胜利的彼岸BE+AE=CE+AE=5(等量代换).AC=AE+EC=5(已知),老师期望:
你能注意学习规范的解题过程.进步的标志′驶向胜利的彼岸你能写出“定理 线段垂直平分线上的点到这条线段两个端点距离相等”的逆命题吗?
逆命题 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.它是真命题吗?如果是.请你证明它.已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.分析:要证明点P在线段AB的垂直平分线上,可以先作出过点P的AB的垂线(或过AB中点的直线,),然后证明另一个结论正确.想一想:若作出∠P的角平分线,结论是否也可以得证?你还有其它证法吗?驶向胜利的彼岸逆定理逆定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.ABL 在京沈高速公路L(秦皇岛段)的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?京 沈 高 速 公 路分析:如图,在直线L上求作一点P,使PA=PB.老师提示 数学问题源于生活实践,反过来数学又为生活实践服务.解:连结AB,作AB的垂直平分线MN与L的交点P即为所求. 线段的垂直平分线求作一点P,使它和已△ABC的三个顶点距离相等.实际问题线段的垂直平分线的作法已知:线段AB,如图.
求作:线段AB的垂直平分线.用尺规作线段的垂直平分线.1.分别以点A和B为圆心,以大于AB/2长为半径作弧,两弧交于点C和D.2. 作直线CD.则直线CD就是线段AB的垂直平分线.请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.作法:回味无穷定理 线段垂直平分线上的点到这条线段两个端点距离相等.
如图,
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
逆定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).挑战自我驶向胜利的彼岸2.已知线段AB外两点C,D,且CA=CB,DA=DB.直线CD交AB于O,则点O是AB的____,CD是AB的________,若直线CD上还有一点E,那么EA与EB的关系是____,你的依据是______________________________.中点垂直平分线相等线段垂直平分线上的点到线段两端点的距离相等B老师期望:
你能说出选择结果的根据.老师期望:
你能说出填空结果的根据.解:AB=AC(已知),△PBQ △QCR(SAS),QP=QR(全等三角形对应边相等).点Q在PR的垂直平分线上.∠B=∠C(等边对等角).挑战自我驶向胜利的彼岸知识的升华祝你成功! 如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长。 板书设计 线段垂直平分线
1、?定理:
线段垂直平分线的性质定理;线段垂直平分线上的点到这条线段两端点的距离相等
2、逆定理:到一条线段两端点距离相等的点在这条线段的垂直平分线上结束寄语严格性之于数学家,犹如道德之于人。
证明的规范性在于:条理清晰,因果相应,言必有据。这是初学证明者谨记和遵循的原则。
