直线与圆的位置关系

课件35张PPT。欢迎加入我们的数学课堂太阳下山了义务教育课程标准实验教科书（冀教版）九年级下册
茶棚乡初级中学 苏英茹35.2直线与圆的位置关系温故而知新（一）(1)两点间的距离(2)点到直线的距离A· ·BC温故而知新（二）点和圆的位置关系是怎样的？点在圆内．P．P点在圆上
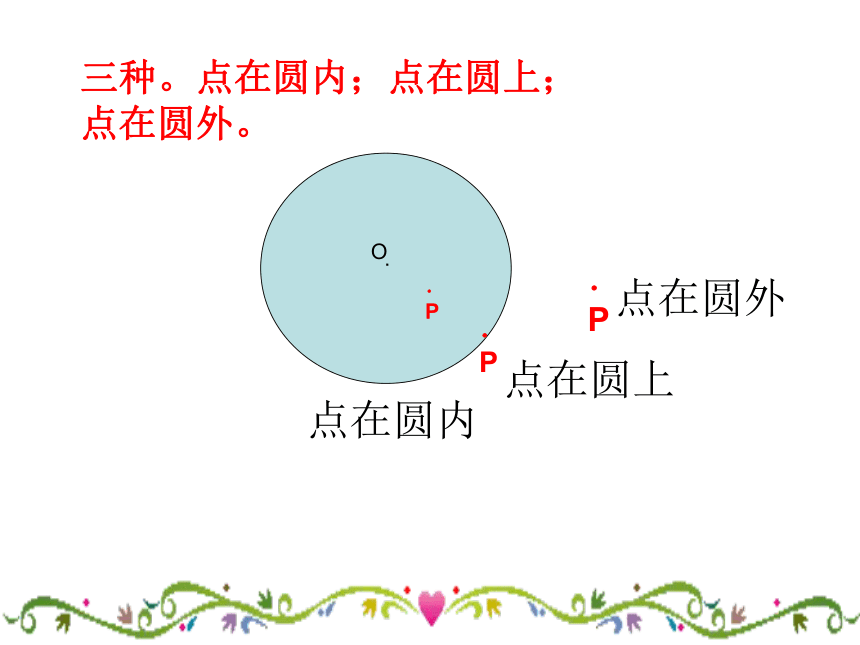
．P点在圆外三种。点在圆内；点在圆上；点在圆外。
点和圆的
位置关系
有三种
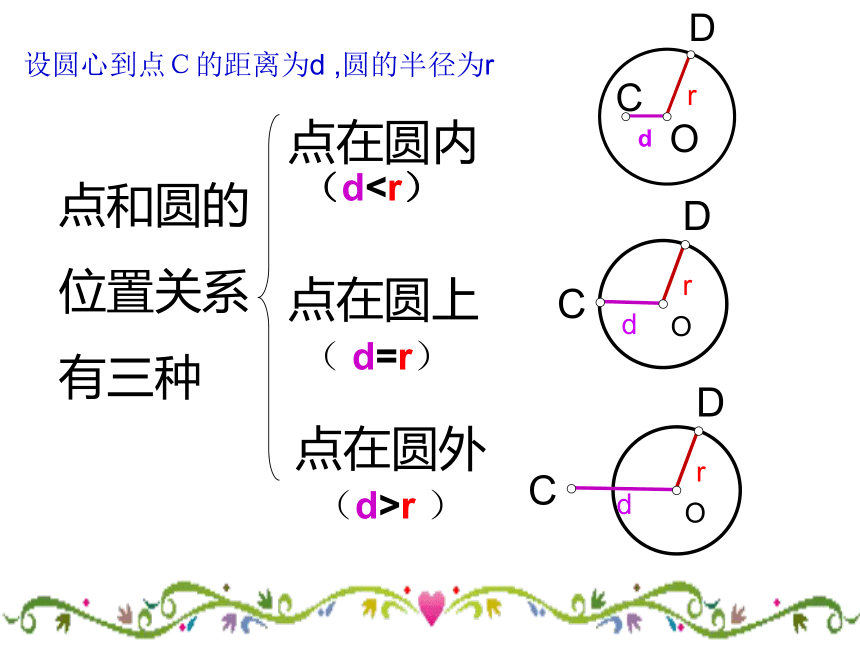
点在圆外点在圆上点在圆内drOCDdrOCDdrOCD设圆心到点Ｃ的距离为d ,圆的半径为r
（d（ d=r）（d>r ）
？猜想、探究：如果把点换成直线呢？首先大家继续看这个情景剧，注意观察这其中体现了直线与圆的哪些位置关系？你到海边看过太阳升起的过程吗？ 直线和圆的位置有
何关系？？？思考：
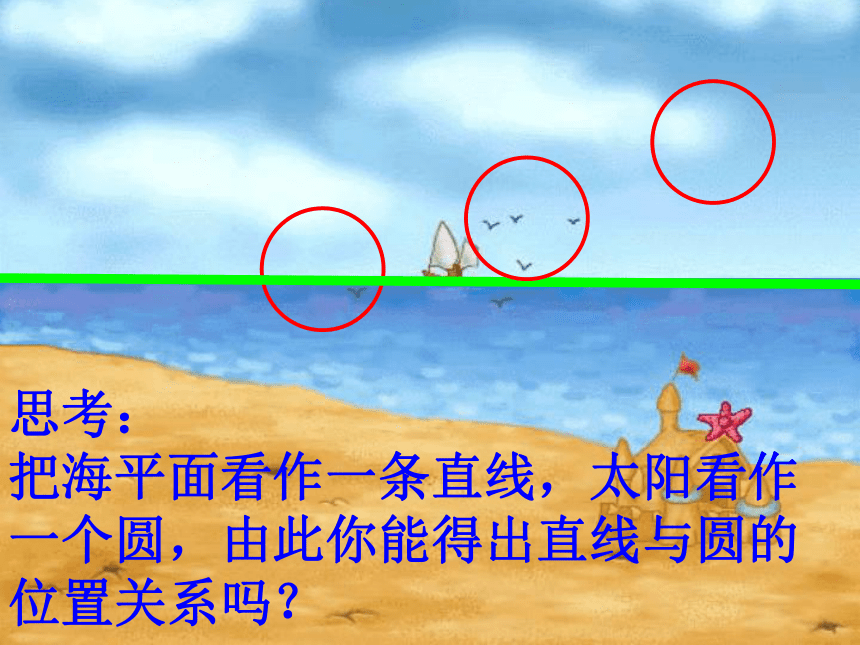
把海平面看作一条直线，太阳看作一个圆，由此你能得出直线与圆的位置关系吗？ 思考：
把海平面看作一条直线，太阳看作一个圆，由此你能得出直线与圆的位置关系吗？ 自制教具演示动画演示启发诱导、探索新知动手实践验证结论【请同学们先画一个圆，再用直尺的一边当直线并任意移动，观察直线和圆的位置关系有几种？】1.直线和圆的位置关系有三种
2.用图形表示如下:.O.O.Olll相离 相切相交切线切点割线...有两个公共点有唯一公共点没有公共点(从直线与圆公共点的个数来判定)讲解 思考：能否根据基本概念来判断直线与圆的位置关系？直线l与⊙O有两个公共点 直线l与⊙O相交．
直线l与⊙O只有一个公共点 直线l与⊙O相切．
直线l与⊙O无公共点 直线l与⊙O相离．1、快速判断下列各图中直线与圆的位置关系ll.O2ll.o学以致用(1)直线与圆最多有两个公共点. （ ） √×(3)若A是⊙O上一点，则直线AB与⊙O相切.( ).A.O(2)若直线与圆相交，则直线上的点都在圆内.( ) (4)若C为⊙O外的一点，则过点C的直线CD与⊙O相交或相离。（ ）××2、判断.C？l 如果，公共点的个数不好判断，该怎么办？·O “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析？·
A·
B启发诱导、探索新知O 是否还有其他的方法判断直线与圆的位置关系？ 设⊙O的半径为r，直线l到圆心O的距离为d，在直线和圆的不同位置关系中，d与r具有怎样的大小关系？
反过来，你能根据d与r的大小关系来确定直线和圆的位置关系吗？ 分组讨论、探究：d>r 直线l与⊙O相离d=r 直线l与⊙O相切d（从左端到右端反映直线与圆的某种位置关系的判定．
从右端到左端反映直线与圆的某种位置关系的性质．）2个交点割线1个切点切线d < rd = rd > r没有归纳总结：判定直线 与圆的位置关系的方法有____种：（1）根据定义，由__________________的个数来判断；（2）根据性质，由___________________________________的关系来判断。在实际应用中，常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r经验累积纸上谈兵老师准备了一些“合同”，需要用你们的智慧来签定“合同”。看谁真正掌握住本节课的知识，能够“金口一开，合同拿来”，未来的“企业家”可能就是你啊！随心所欲一个同学说出一个圆的半径和圆心到直线的距离随机找另一个同学说出这条直线和圆的位置关系,我们集体作为老师给判断。例题讲解例 在Rt?ABC中, ?C=90°, AC=3cm, BC=4cm, 以C为圆
心, r 为半径的圆与AB有怎样的位置关系? 为什么?
(1) r =2cm ; (2) r =2.4cm ; (3) r =3cm.ABDC(1)DBC(2)ACBD(3)解：过C作CD⊥AB，垂足为D（如上图）.在Rt?ABC中,根据勾股定理
得:AB=5cm. 再根据三角形的面积公式有 CD·AB=AC·BC,
∴CD=2.4cm 即圆心C到AB的距离d=2.4cm.(1) 当 r = 2cm时, 有 d > r, 因此?C和AB相离.(2) 当 r = 2.4cm时, 有 d = r, 因此?C和AB相切.(3) 当 r = 3cm时, 有 d < r, 因此?C和AB相交. 分析：因为题目给出了⊙O的半径，所以解题关键是求圆心C到直线AB的距离，也就是要求出Rt△ABC斜边AB上的高.因此,可过C点向AB作垂线段CD，然后根据CD的长度与r进行比较，来确定⊙C与AB的关系. √√√小试牛刀判断：
1、直线和圆有公共点,这条直线叫做圆的割线.( )
2、直线和圆有公共点,这条直线叫做圆的切线.( )
3、直线和圆相切,直线和圆有唯一的公共点. ( )
4、圆心到直线的距离等于半径,这条直线叫圆的切线. ( )
5、直线过圆上一点，这时直线是圆的切线。( )
6、直线是圆的切线，必须在直线上有唯一的点到圆心距离等于半径。( )
7、直线过圆外两点，这时直线与圆相离。( )
8、已知⊙O的半径为4cm，直线l上的点A满足OA=4cm，所以直线l和⊙O相切。( )填空：
已知⊙O的直径为13cm，若直线l与圆心O的距离d=4.5cm时，直线与圆的位置关系是___________，有________个交点，此时直线叫圆的_________；
当d=6.5cm时，直线与圆的位置关系是________，有_________个交点，此时直线叫圆的__________.
当d=8cm时，直线与圆的位置关系是________，有_____个交点。 相切210相交割线切线相离挑战自我1、设⊙O的半径为r，点O到直线a的距离为d，
若⊙O与直线a至多只有一个公共点，则d与r的
关系是……………………（ ）
A、d≤r B、d＜r C、d≥r D、d＝r2、设⊙O的半径为r，直线a上一点到圆心的
距离为d，若d=r，则直线a与⊙O的位置关系
是……………………………………………（ ）
A、相交 B、相切 C、相离 D、相切或相交CD挑战极限（１）圆心O到直线l的距离为d,⊙O的半径为R，若d、R是方程x2－4x＋m＝0的两根，且直线l与⊙O相切，则m的值是________．（2006.山东）（２）设⊙O的半径为r,点O到直线l的距离为d,若⊙O与l最多只有一个公共点，则d与r的关系为_________.（2005.河北）d≥ r中　考　考　场4你说，我说，大家一起说！通过本节课的学习，你掌握了哪些知识？谈谈你本节课的收获：相离 0——d>r直线1个 切点d=r切线2个交点d过点A作AB⊥MN于点B.在Rt△ABP中， ∠APN＝30o, AP＝160m，所以AB= 80m. ∵ AB<100 ∴学校受噪音的影响.在MN上取AC=AD=100m.
在Rt△ABC中, ∵ AB= 80m, AC=100m, ∴BC=60m.同理,BD=60m. ∴120÷18=20/3秒.
∴学校受影响的时间为20/3秒.数学与生活课外作业巩固性作业：
课本第40页第4、5题
研究体验性练习：
1、完成39页练习题
2、课余时间，留心观察周围事物，找出直线和圆相交，相切，相离的实例，说给大家听。
预习性作业：
35.3 切线的画法、判定和性质。结束寄语悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.愿你拥有一个能用数学思维思考世界的头脑。一双能用数学视觉观察世界的眼睛；讨论在Rt△ABC中，∠C=90°，AC=3cm，
BC=4cm，以C为圆心，r为半径作圆．1、当r满足________________时，
⊙C与直线AB相离．2、当r满足____________ 时，
⊙C与直线AB相切．3、当r满足____________时，
⊙C与直线AB相交．BCAD45d=2.4cm30cm