12.3.2等边三角形
图片预览


文档简介
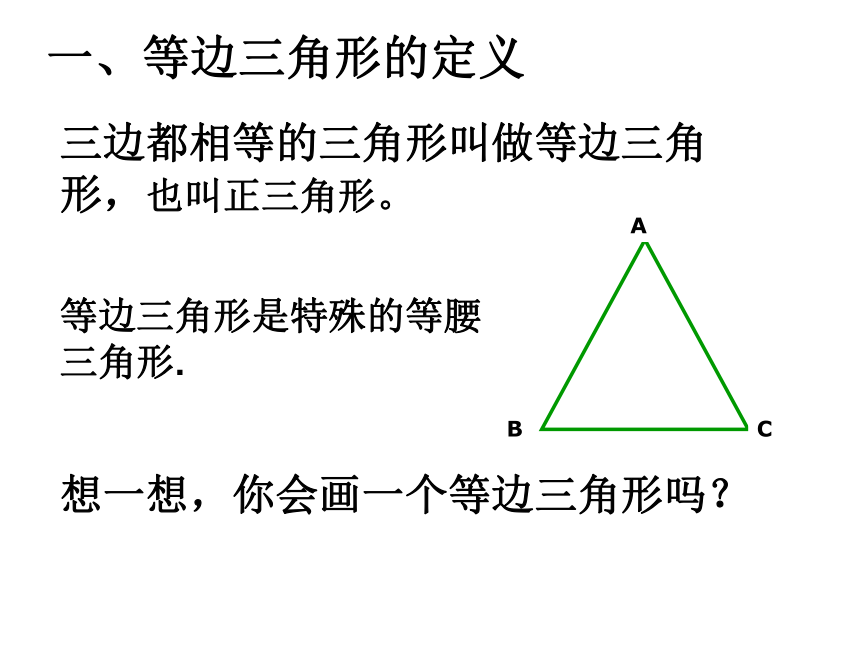
课件22张PPT。观察下列图片,找出你熟悉的图形.12.3.2等边三角形我思考 我进步一、等边三角形的定义三边都相等的三角形叫做等边三角形,也叫正三角形。想一想,你会画一个等边三角形吗?等边三角形是特殊的等腰三角形.开启 智慧 一. 等边三角形是特殊的等腰三角形,那么等腰三角形的所有性质是否都适用于等边三角形呢?
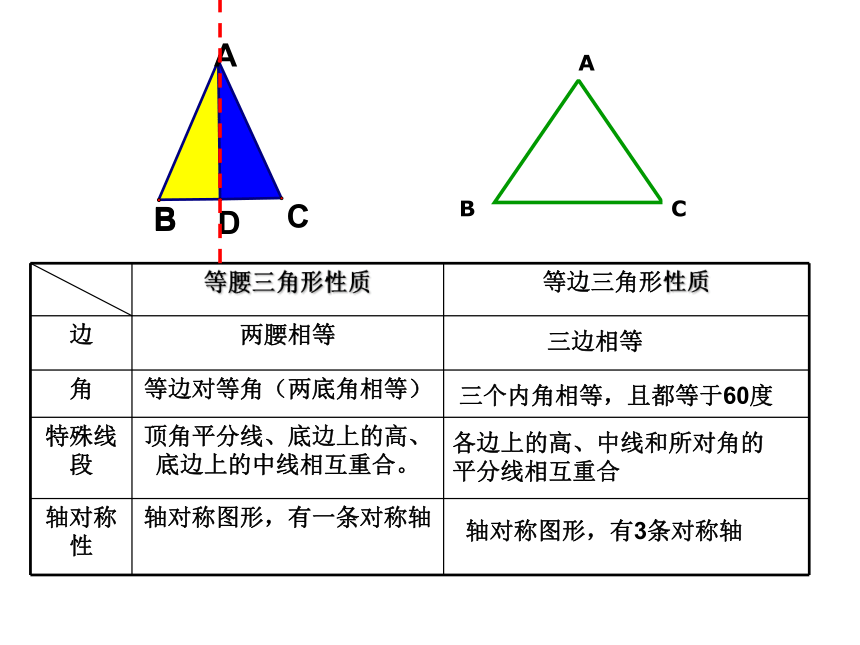
等边三角形还有哪些性质呢?1等腰三角形的所有性质都适用于等边三角形。三边相等三个内角相等,且都等于60度各边上的高、中线和所对角的平分线相互重合轴对称图形,有3条对称轴二.如何判定一个三角形是等边三角形?三个角都相等的三角形是否是等边三角形?求证:三个角都相等的三角形是等边三角形.已知:如图,在△ABC中,∠A=∠B=∠C.
求证:△ABC是等边三角形.开启 智慧已知: △ABC中, AB=AC,并且有一个角为60 °,
求证: △ABC是等边三角形
60°你认为有一个角是600的等腰三角形是等边三角形吗?你能证明你的结论吗?
求证:。开启 智慧求证:有一个内角等于60 °的等腰三角形是等边三角形.
已知: △ABC中, AB=AC,并且有一个角为60 °
求证: △ABC是等边三角形
证明: ∵ AB=AC. ∴ ∠ B= ∠ C
(1)当顶角∠A=60 °时,
(2)当底角∠ B= 60 °时,
善于归纳一、等边三角形的性质二. 等边三角形的判定1、三边相等的三角形是等边三角形。(定义)
2、三个角都相等的三角形是等边三角形。
3、有一个内角等于60 °的等腰三角形是等边三角形.1.等边三角形的三边相等。(定义)
2.等边三角形的三个内角都相等,并且每一个角都等于600.
3.等边三角形各边上的高线、中线和它对角的平分线相互重合。
4.等边三角形是轴对称图形,它有三条对称轴.理解定理,融会贯通例1、如图△ABC是等边三角形,DE∥BC,交AB、AC于D、E。
求证:△ADE是等边三角形。 应用定理60°60°60°60°60°练习:如图,等边三角形ABC中,AD是BC上的高.∠ BDE=∠CDF=60 °,图中与BD相等的线 段 . 巧用定理你准备好了吗?练习:如图,等边三角形ABC中,AD是BC上的高.∠ BDE=∠CDF=60 °,图中
与BD相等的线 段 BE、DE、DF、FC、DC、AE、AF .
请找出图中的所有等边三角形。60°已知:D、E、F分别是等边△ABC各边上的一点,且AD=BE=CF.
试说明△ DEF是等边三角形.
变式1如图, △ABC为等边三角形,∠ 1= ∠ 2= ∠ 3
△DEF为等边三角形吗?为什么?变式2?如图, D、E、F分别是等边△ABC各边的延长线上的点,当满足什么条件时△DEF为等边三角形.课后思考等边三角形与等腰三角形在定义,性质和判定的异同.有二条边相等1、两个底角相等
2、三线合一
3、对称轴一条1、三个角都相等
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、三个角都相等
3、等腰三角形有
一个角是600本节课你学到了哪些知识?教师寄语愿你用勤奋的汗水
浇灌智慧的花朵谢谢老师们
光临指导!已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F.MN(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?(4)MN与BC平行吗?为什么?
(5)若△ABD绕B点旋转,在旋转过程中AE与CD相等吗?画出图形证明.性质我们一起回忆:两个底角相等两腰相等判定顶角平分线、底边上的高线和中线相互重合两边相等的三角形是
等腰三角形。有两个角相等的三角形是等腰三角形。等腰三角形是轴对称图形,对称轴是顶角平分线(或底边上的中线或底边上的高)所在的直线。边角主要
线段
等边三角形还有哪些性质呢?1等腰三角形的所有性质都适用于等边三角形。三边相等三个内角相等,且都等于60度各边上的高、中线和所对角的平分线相互重合轴对称图形,有3条对称轴二.如何判定一个三角形是等边三角形?三个角都相等的三角形是否是等边三角形?求证:三个角都相等的三角形是等边三角形.已知:如图,在△ABC中,∠A=∠B=∠C.
求证:△ABC是等边三角形.开启 智慧已知: △ABC中, AB=AC,并且有一个角为60 °,
求证: △ABC是等边三角形
60°你认为有一个角是600的等腰三角形是等边三角形吗?你能证明你的结论吗?
求证:。开启 智慧求证:有一个内角等于60 °的等腰三角形是等边三角形.
已知: △ABC中, AB=AC,并且有一个角为60 °
求证: △ABC是等边三角形
证明: ∵ AB=AC. ∴ ∠ B= ∠ C
(1)当顶角∠A=60 °时,
(2)当底角∠ B= 60 °时,
善于归纳一、等边三角形的性质二. 等边三角形的判定1、三边相等的三角形是等边三角形。(定义)
2、三个角都相等的三角形是等边三角形。
3、有一个内角等于60 °的等腰三角形是等边三角形.1.等边三角形的三边相等。(定义)
2.等边三角形的三个内角都相等,并且每一个角都等于600.
3.等边三角形各边上的高线、中线和它对角的平分线相互重合。
4.等边三角形是轴对称图形,它有三条对称轴.理解定理,融会贯通例1、如图△ABC是等边三角形,DE∥BC,交AB、AC于D、E。
求证:△ADE是等边三角形。 应用定理60°60°60°60°60°练习:如图,等边三角形ABC中,AD是BC上的高.∠ BDE=∠CDF=60 °,图中与BD相等的线 段 . 巧用定理你准备好了吗?练习:如图,等边三角形ABC中,AD是BC上的高.∠ BDE=∠CDF=60 °,图中
与BD相等的线 段 BE、DE、DF、FC、DC、AE、AF .
请找出图中的所有等边三角形。60°已知:D、E、F分别是等边△ABC各边上的一点,且AD=BE=CF.
试说明△ DEF是等边三角形.
变式1如图, △ABC为等边三角形,∠ 1= ∠ 2= ∠ 3
△DEF为等边三角形吗?为什么?变式2?如图, D、E、F分别是等边△ABC各边的延长线上的点,当满足什么条件时△DEF为等边三角形.课后思考等边三角形与等腰三角形在定义,性质和判定的异同.有二条边相等1、两个底角相等
2、三线合一
3、对称轴一条1、三个角都相等
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、三个角都相等
3、等腰三角形有
一个角是600本节课你学到了哪些知识?教师寄语愿你用勤奋的汗水
浇灌智慧的花朵谢谢老师们
光临指导!已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F.MN(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?(4)MN与BC平行吗?为什么?
(5)若△ABD绕B点旋转,在旋转过程中AE与CD相等吗?画出图形证明.性质我们一起回忆:两个底角相等两腰相等判定顶角平分线、底边上的高线和中线相互重合两边相等的三角形是
等腰三角形。有两个角相等的三角形是等腰三角形。等腰三角形是轴对称图形,对称轴是顶角平分线(或底边上的中线或底边上的高)所在的直线。边角主要
线段
