锐角三角函数的应用

课件19张PPT。宇宙之大，粒子之微，
火箭之速，化工之巧；
地球之变，生物之谜，
日用之繁，无处不用数学。——华罗庚31.3锐角三角函数的应用茶棚中学 苏英茹复习提问三个锐角三角函数的表示方法：
正弦：
余弦：
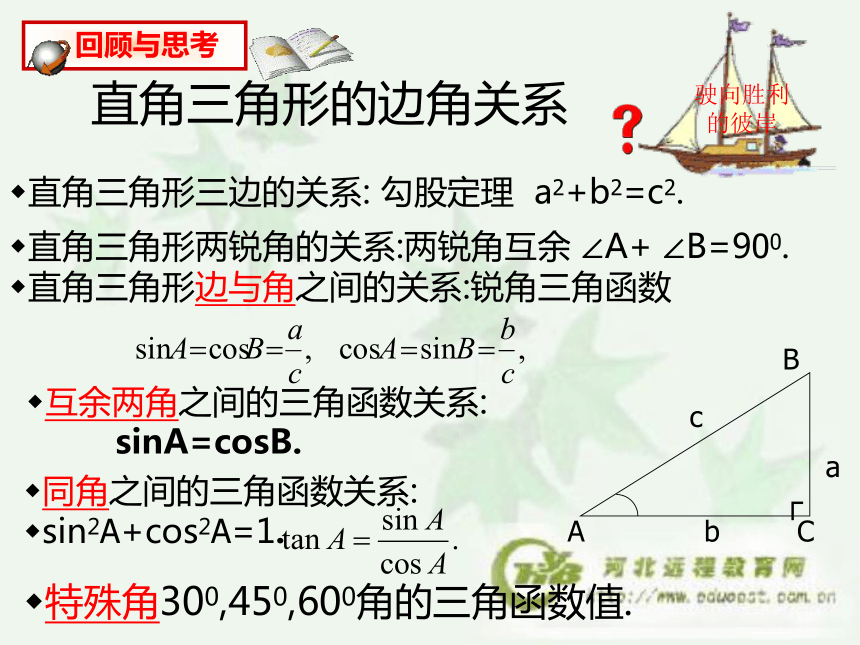
正切：直角三角形两锐角的关系:两锐角互余 ∠A+ ∠B=900.直角三角形的边角关系直角三角形三边的关系: 勾股定理 a2+b2=c2.互余两角之间的三角函数关系:
sinA=cosB.特殊角300,450,600角的三角函数值.直角三角形边与角之间的关系:锐角三角函数同角之间的三角函数关系:
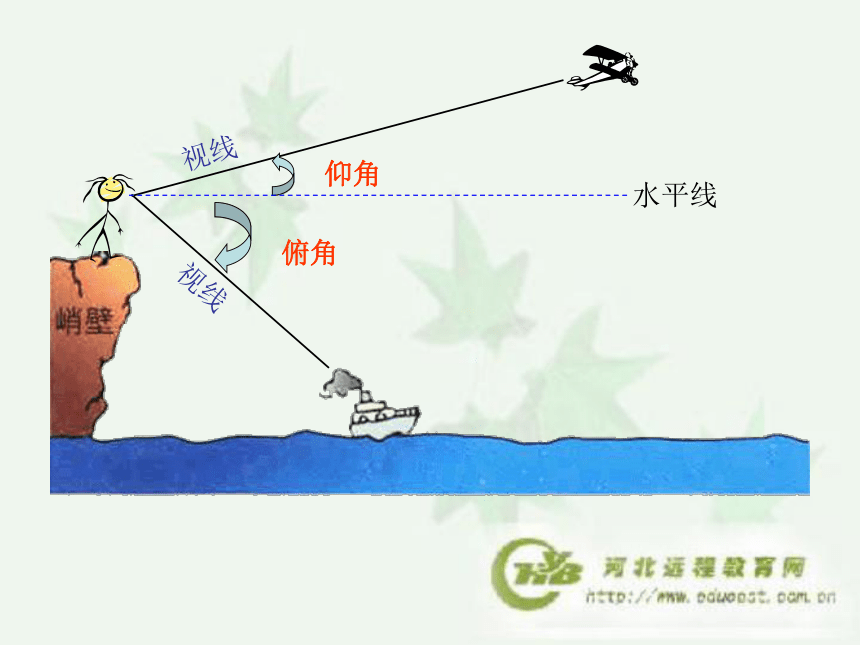
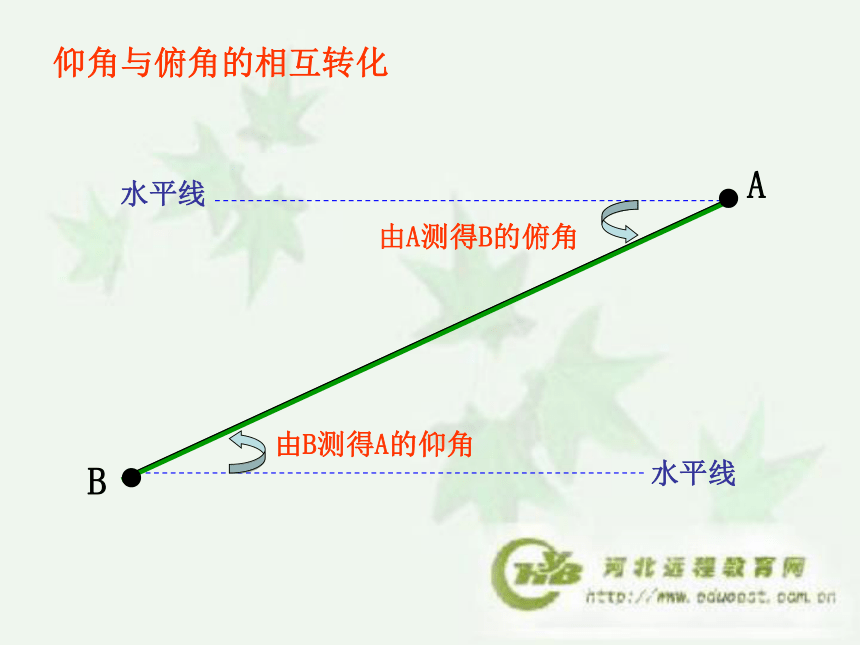
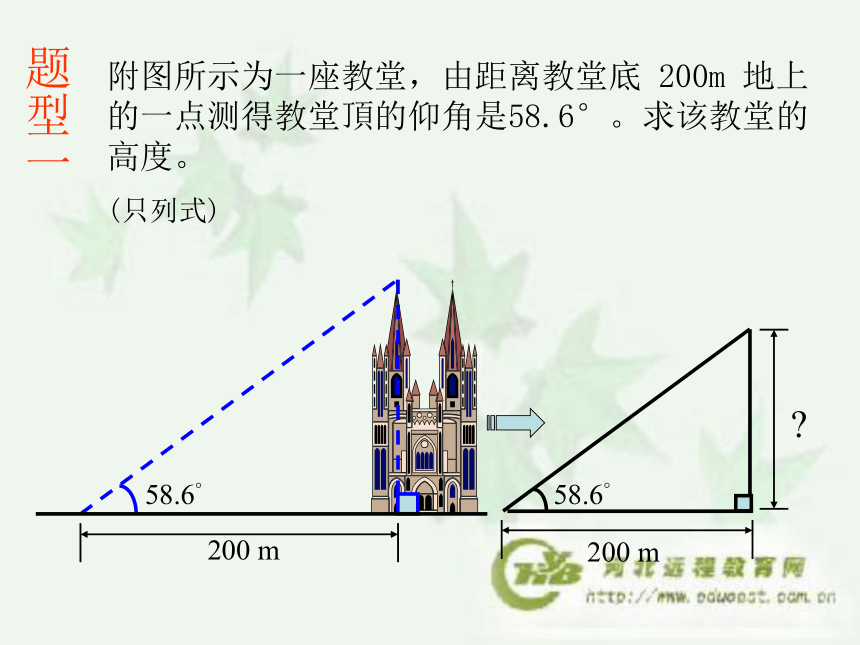
sin2A+cos2A=1.俯角仰角水平线视线视线由A测得B的俯角由B测得A的仰角水平线水平线仰角与俯角的相互转化58.6°200 m附图所示为一座教堂，由距离教堂底 200m 地上的一点测得教堂頂的仰角是58.6°。求该教堂的高度。
(只列式)58.6°200 m题型一步骤:如右图标明，
= tan 58.6°
h = 200 x tan 58.6°

58.6°200 m 如图,当奇奇乘坐登山缆车的吊箱研某条直线经过点A到达点B时,它走过了200m. 在这段路程中由A点看B点的仰角为30°,你知道缆车垂直上升的距离是多少吗?ABABD30°200真挚在实践中产生ABC 当奇奇要乘缆车继续从点B到达比点B高 200m的点C, 如果这段路程由B点看C点的仰角为60°,缆车行进速度为1m/s,奇奇需要多长时间能到达目的地？ABDCE拓展一60°200如图，一艘渔船正以30海里/时的速度由西向东追赶鱼群，在A处看见小岛C在船北偏东60°的方向上；40min后，渔船行驶到B处，此时小岛C在船北偏东30°的方向上。已知以小岛C为中心，10海里为半径的范围内是多暗礁的危险区。这艘渔船如果继续向东追赶鱼群，有没有进入危险区的可能？(实际问题先数学化) 题型二船有无危险一起探究： 3．在什么条件下，渔船才会驶入危险区？1．A，B两点间的距离是多少？2．怎样计算小岛C到航线AB的距离？D船有无触礁的危险如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.要解决这个问题,我们可以将其数学化,如图:请与同伴交流你是怎么想的? 怎么去做?你认为货轮继续向东航行途中会有触礁的危险吗?联想的功能你说，我说，大家一起说！通过本节课的学习，你掌握了哪些知识？谈谈你本节课的收获：由特殊锐角的三角函数值反求锐角填表:已知一个角的三角函数值,求这个角的度数(逆向思维)回味无穷试一试谁拥有“火眼”分组到网上去寻找锐角三角函数应用的相关习题，并把它记下来，课下组内完成它。看哪组找到的类型题多并且完成的也好，有外的收获啊，请拭目以待吧！P121 习题 2题;
祝你成功！结束寄语悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.愿你拥有一个能用数学思维思考世界的头脑。一双能用数学视觉观察世界的眼睛；