平行线的性质(无答案)

平行线的性质
1、 教学目标：通过实际操作，探索平行线的性质。
会运用平行线的性质，解决与“三线八角”有关的计算问题。
2、 重难点：会利用平行线的性质解决一些实际问题。
3、 教学过程：
自主探究
1.学生画图活动:两条平行线a∥b,再画一条截线c与直线a、b相交,标出所形成的八角
2.学生测量这些角的度数,把结果填入表内.
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
3.学生根据测量所得数据作出猜想.
图中哪些角是同位角 它们具有怎样的数量关系
图中哪些角是内错角 它们具有怎样的数量关系
图中哪些角是同旁内角 它们具有怎样的数量关系
4. 能否将我们发现的结论给予较为准确的文字表述
平行线具有性质:
性质1: .
性质2: .
性质3: .
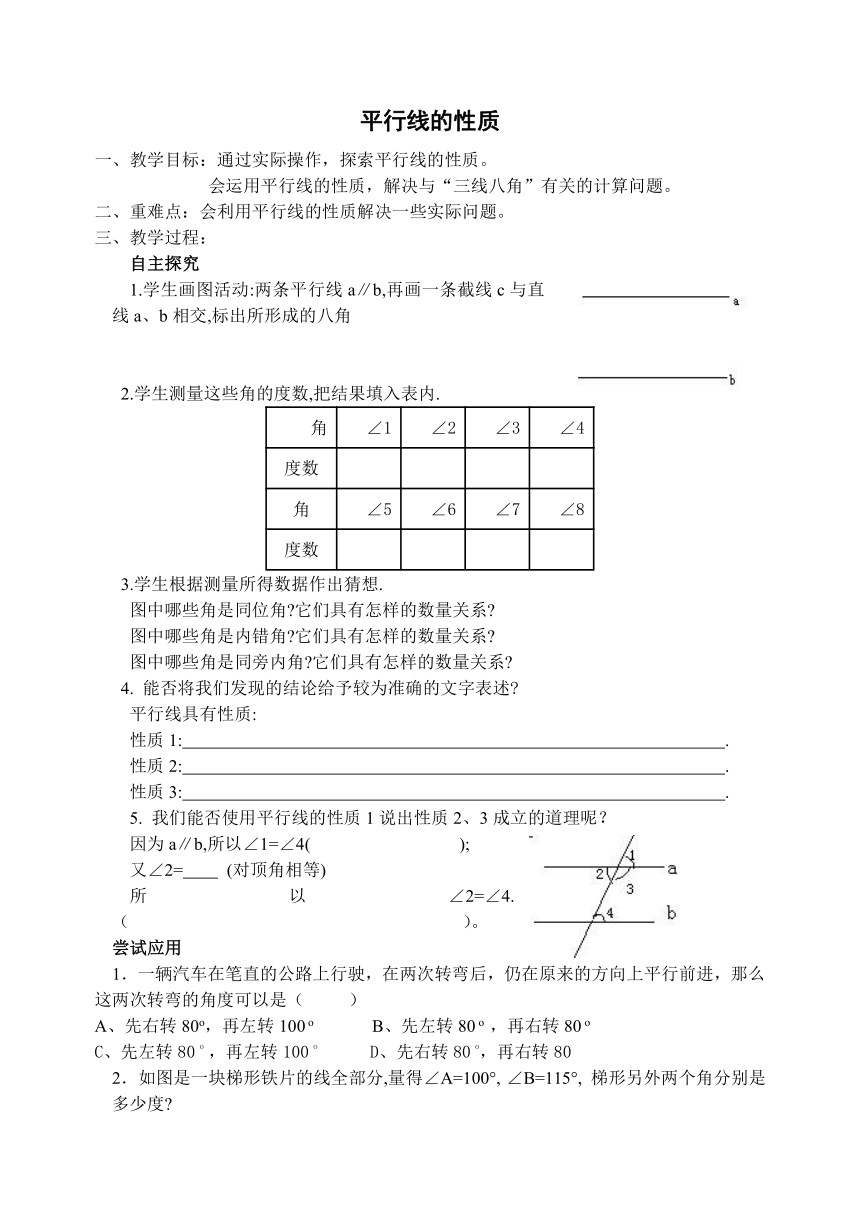
5. 我们能否使用平行线的性质1说出性质2、3成立的道理呢？
因为a∥b,所以∠1=∠4( );
又∠2= (对顶角相等)
所以∠2=∠4.（ ）。
尝试应用
1．一辆汽车在笔直的公路上行驶，在两次转弯后，仍在原来的方向上平行前进，那么这两次转弯的角度可以是（ ）
A、先右转80o，再左转100 o 　　　B、先左转80 o ，再右转80 o
C、先左转80 o ，再左转100 o　　　D、先右转80 o，再右转80
2．如图是一块梯形铁片的线全部分,量得∠A=100°, ∠B=115°, 梯形另外两个角分别是多少度
课堂展示
1、如图7，已知，AB∥CD，EF交AB，CD于G，H，GM，HN分别平分∠AGF，∠EHD.试说明GM∥HN.
2、∠1和∠2是直线AB、CD被直线EF所截而成的内错角,那么∠1和∠2 的大小关系是( )
A.∠1=∠2 B.∠1>∠2; C.∠1<∠2 D.无法确定
3、判断题
(1).两条直线被第三条直线所截,则同旁内角互补.( )
(2).两条直线被第三条直线所截,如果同旁内角互补,那么同位角相等.( )
(3).两条平行线被第三条直线所截,则一对同旁内角的平分线互相平行.( )
拓展提高
1.:如图,BCD是一条直线,∠A=75°,∠1=53°,∠2=75°,求∠B的度数.
2.如图,已知:∠1=110°,∠2=110°,∠3=70°,求∠4的度数.
3． 如图10，直线a／／b，点B在直线b上，且AB ⊥BC ,∠1 = 55 ，则∠2 的度数为 ( ) D .
A . 35 B . 45 C . 55 D . 125
4.已知:如图11,AB∥CD.
求证: ∠D+∠E+∠B=360°.
作业
1.课本23页练习习题。
A
B
C
E
D
F
G
H
M
N
1
2
图7
图10
图11
B
A
C
D
E
PAGE