苏州市某重点中学八年级数学阶段练习试题

苏州市某重点中学八年级数学阶段练习试题
1、 细心选一选
(本题有9小题，每小题3分，共27分.）
1．下列图形中，不是轴对称图形的是 （ ）
A.　 B.　 C.　 D.　
2．如图， BE、CF分别是△ABC的高，M为BC的中点， EF=5，BC=8，则△EFM的周长是（ ）
A、21 B、18 C、13 D、15
3、在实数－，0，，－3.14，， 中，无理数有( )
A 1个 B 2个 C 3个 D. 4个
4、16的平方根是（ ）
A.±4 B.4 C.±2 D.2
5、、化简的结果是 （ ）
A． B． C． D．2
6、下列各组数中不能作为直角三角形的三边长的是（ ）
A. 2, 3，4; B. 7, 24, 25; C. 6, 8, 10; D. 9, 12, 15.
7、△ABC中，①若AB＝BC＝CA，则△ABC是等边三角形；②一个底角为60°的等腰三角形是等边三角形；③顶角为60°的等腰三角形是等边三角形;④有两个角都是60°的三角形是等边三角形．上述结论中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
8．对于四舍五入得到的近似数4.70×104，下列说法正确的是（ ）
A．有3个有效数字，精确到百分位 B．有5个有效数字，精确到个位 C．有2个有效数字，精确到万位　 D．有3个有效数字，精确到百位
9．如图，在Rt△ABC 中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△绕点顺时针旋转90后，得到△，连接．下列结论中正确的个数有（ ）
① ②△≌△
③平分 ④
A．１个　 B．２个　 C．３个　　 D．４个　　
二、专心填一填（每题3分，共18分）
10、等腰三角形的一个外角是130°，则它的底角等于 ；
11、写出一个3到4之间的无理数 。
12、已知，在△ABC中，∠A= 45°，AC= ，AB= +1，则边BC的长为 ．
( http: / / )
13．在一个长为2米，宽为1米的矩形草地上，如图堆放着一根长方体的木块，它的棱长和场地宽AD平行且大于AD，木块的正视图是边长为0.2米的正方形，一只蚂蚁从点A处，到达C处需要走的最短路程是 米.
14、若a，b都是无理数，且a＋b＝2，则a，b的值可以是 （填上两组满足条件的值即可）．
15、如下图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若，，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是 ．
三、耐心答一答（本题共52分，解答时必须写明演算过程、说理过程或必要的文字说明。）
16、（6分）求下列各式中的实数x.
(1) (x＋10)＝－27； (2) =25
17、作图题（6分）：
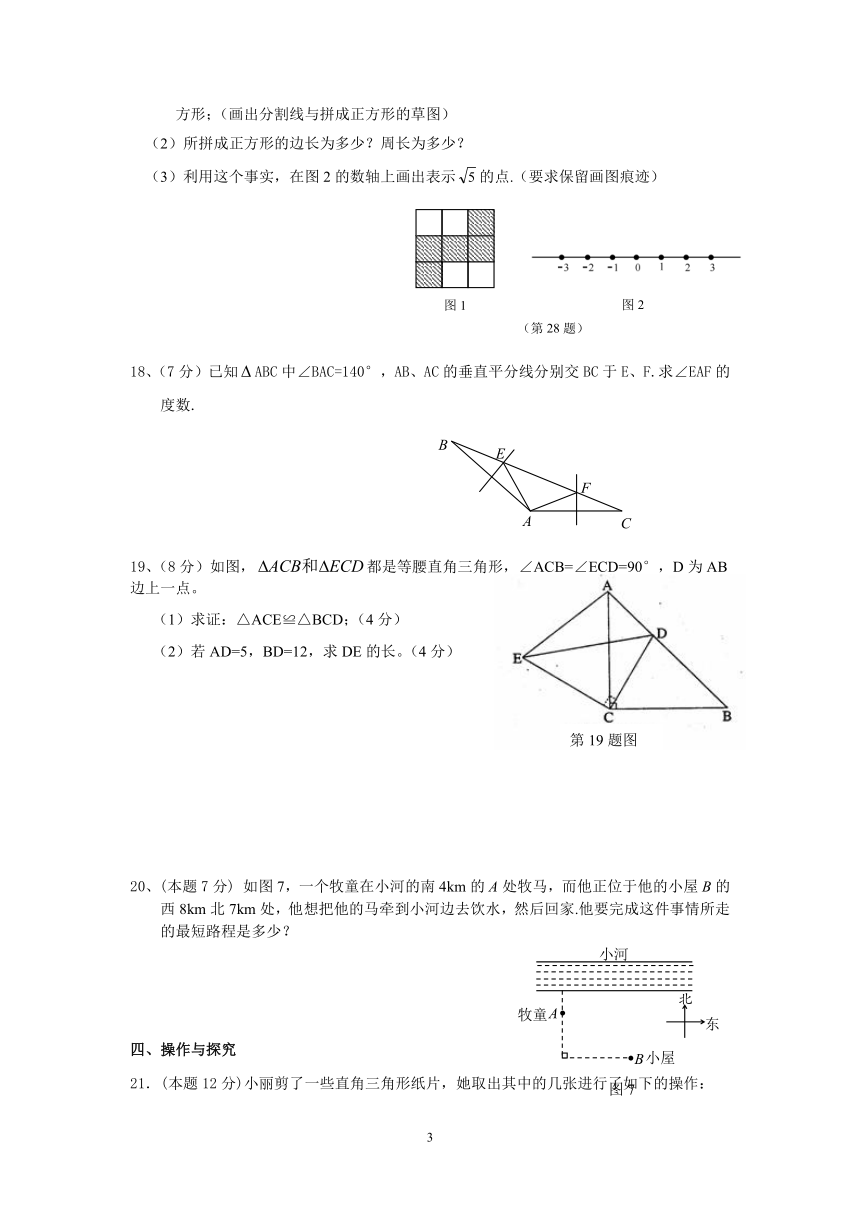
如图1是单位为1的方格图. （1）请把方格图中的带阴影的图形适当剪开，重新拼成正方形；（画出分割线与拼成正方形的草图）
（2）所拼成正方形的边长为多少？周长为多少？
（3）利用这个事实，在图2的数轴上画出表示的点.（要求保留画图痕迹）
18、（7分）已知ABC中∠BAC=140°，AB、AC的垂直平分线分别交BC于E、F.求∠EAF的度数.
( http: / / )
19、（8分）如图，都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点。 全品中考网
（1）求证：△ACE≌△BCD；（4分）
（2）若AD=5，BD=12，求DE的长。（4分）
20、(本题7分) 如图7，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家.他要完成这件事情所走的最短路程是多少？
四、操作与探究
21．(本题12分)小丽剪了一些直角三角形纸片，她取出其中的几张进行了如下的操作：
操作一：如图，将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE.
⑴如果AC=6cm,BC=8cm,试求△ACD的周长.
⑵如果∠CAD:∠BAD=4:7,求∠B的度数.
操作二：如图，小丽拿出另一张Rt△ABC纸片，将直角边AC沿直线AD折叠，使它落在斜边AB上,且与AE重合,已知两直角边AC=6cm，BC=8cm，你能求出CD的长吗？
操作三：如图，小丽又拿出另一张Rt△ABC纸片，将纸片折叠，折痕CD⊥AB。
你能证明：BC2+AD2=AC2+BD2 吗？
22. (本题9分)为美化环境，计划在某小区内用30平方米的草皮铺设一块有一边长为10米的等腰三角形绿地，请你求出这个等腰三角形绿地的另两边长.（结果精确到0.1米）
答案
一、细心选一选：
1.C 2.C 3.A 4.A 5.C 6.A 7.D 8.D 9.C
10.50或65 11. 12.2 13.2.6 14.答案不止一个 15.76
16.（1）x=-13 （2）x=或
17．
（1）如图1，…………………………………………………………………………2分
（2）边长为，周长为4……………………………………………………………2分
（3）如图2，………………………………………………………………………………2分
18.设∠B=x ∠C=y 可得x+y=40 所以∠EAF=∠BAC-（x+y）=140-40=100
19.（1）可用“角边角”证得△ACE≌△BCD
（2）由△ACE≌△BCD可得AE=BD=12，在Rt△AED中，由勾股定理得：
DE=
20．如图，作出A点关于MN的对称点A′，连接A′B交MN于点P，
则A′B就是最短路线.在Rt△A′DB中，由勾股定理求得A′B＝17km.
21.操作一：
(1)由对称性可得AD=BD,∵△ACD的周长=AC+CD+AD ∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14(㎝)
(2) 设∠CAD=4x ， ∠BAD=7x 由题意得方程：7x+7x＋4x=90 解之得 x =5
所以∠B=35
操作二：
设CD= x 则BD=8－x DE=x 由题意可得方程
解之得 x=3 所以 CD=3㎝
操作三：
在Rt△BCD中，由勾股定理可得
在Rt△ACD中，由勾股定理可得 AD2＋CD2= AC2
∴BC2+AD2= ＋ AD2= AC2+BD2
22．设△ABC为面积为30m2的等腰三角形，且AB=10m，过C作CH⊥AB于点H.
（1）如图1，AC=10.0m，BC=≈6.3m；………………………………………………3分
（2）如图2，AC=BC=≈7.8m； ………………………………………………………3分
（3）如图3，BC=10，AC=≈19.0m. …………………………………………………3分
（第2题）
（第13题）
A
B
C
图1
图2
图1
图2
（第28题）
第19题图
A
B
小河
东
北
牧童
小屋
图7
B
A
C
D
图1
图2
（第28题答案）
A
B
D
P
N
A′
M
（第32题答案）
（图1）
（图2）
（图3）
PAGE
1