(苏教版选修2-3)数学:3.2《 回归分析》课件
文档属性
| 名称 | (苏教版选修2-3)数学:3.2《 回归分析》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 247.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-27 08:10:00 | ||
图片预览






文档简介
课件20张PPT。3.1回归分析的基本思想及其初步应用 比《数学3》中“回归”增加的内容数学3——统计
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题选修2-3——统计案例
引入线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用
利用线性回归模型解决一类非线性回归问题
正确理解分析方法与结果复习回顾2、数据点和它在回归直线上相应位置的差异 是随机误差的效应,称 为残差。3、对每名女大学生计算这个差异,然后分别将所得的值平方后加起来,用数学符号表示为:
称为残差平方和,它代表了随机误差的效应。4、两个指标:
(1)类比样本方差估计总体方差的思想,可以用作
为 的估计量, 越小,预报精度越高。(2)我们可以用相关指数R2来刻画回归的效果,其
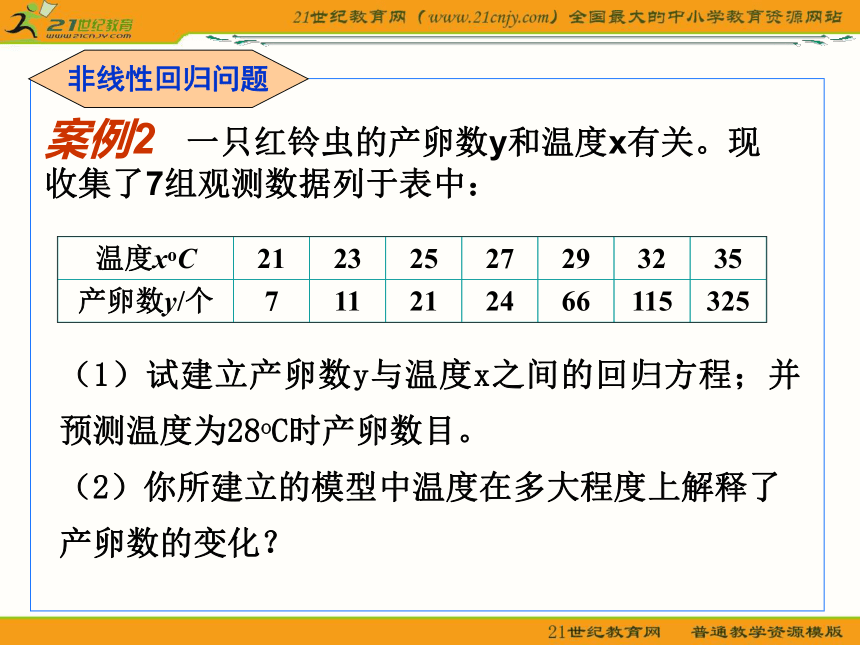
计算公式是: R2 ?1,说明回归方程拟合的越好;R2?0,说明回归方程拟合的越差。 在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否线性相关,是否可以用回归模型来拟合数据。5、残差分析与残差图的定义: 然后,我们可以通过残差 来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析。 我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。案例2 一只红铃虫的产卵数y和温度x有关。现收集了7组观测数据列于表中:(1)试建立产卵数y与温度x之间的回归方程;并预测温度为28oC时产卵数目。
(2)你所建立的模型中温度在多大程度上解释了产卵数的变化?
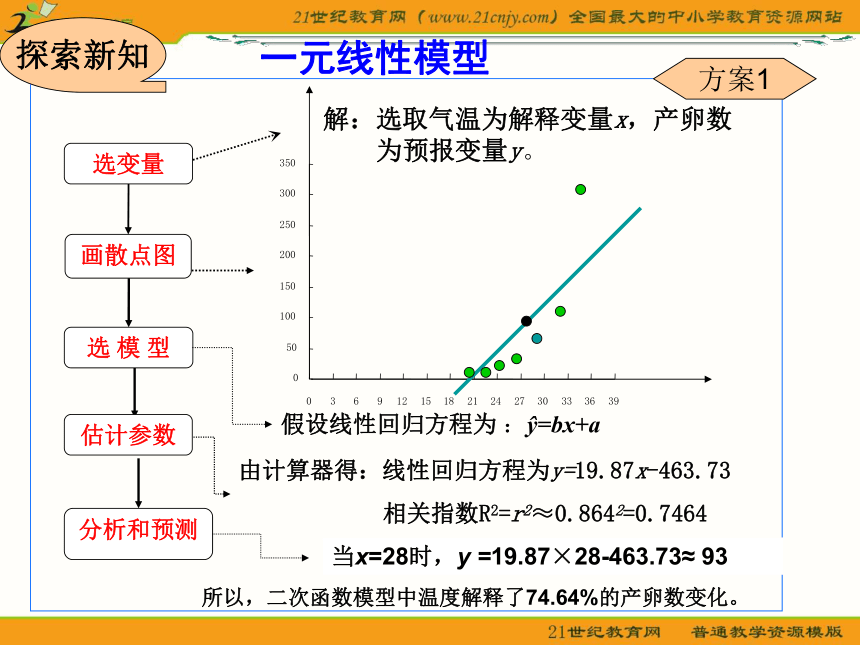
非线性回归问题假设线性回归方程为 :?=bx+a选 模 型由计算器得:线性回归方程为y=19.87x-463.73
相关指数R2=r2≈0.8642=0.7464估计参数
解:选取气温为解释变量x,产卵数
为预报变量y。所以,二次函数模型中温度解释了74.64%的产卵数变化。探索新知方案1分析和预测当x=28时,y =19.87×28-463.73≈ 93一元线性模型奇怪?93>66 ?
模型不好?
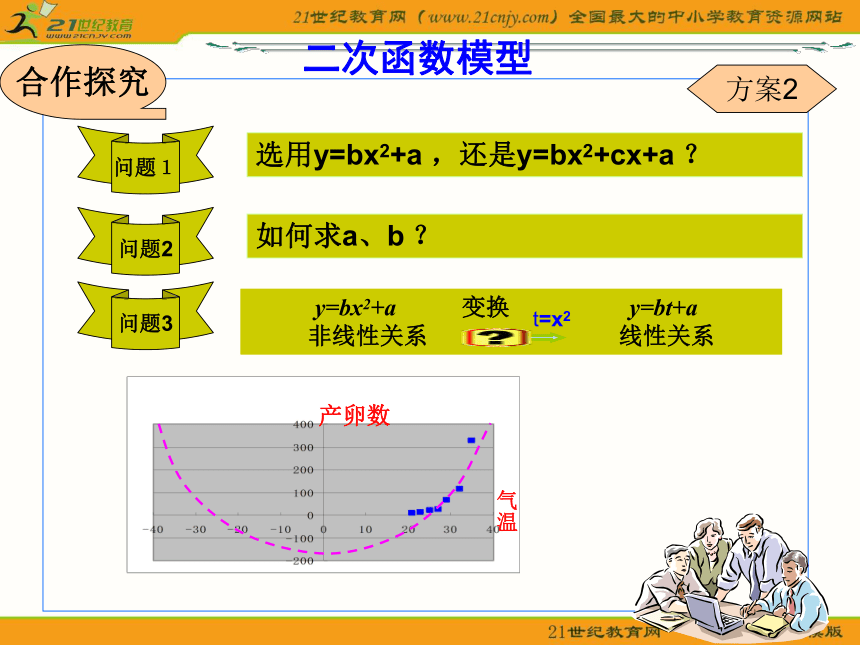
方案2问题3合作探究 t=x2二次函数模型
方案2解答平方变换:令t=x2,产卵数y和温度x之间二次函数模型y=bx2+a就转化为产卵数y和温度的平方t之间线性回归模型y=bt+a作散点图,并由计算器得:y和t之间的线性回归方程为y=0.367t-202.543,相关指数R2=0.802将t=x2代入线性回归方程得:
y=0.367x2 -202.543
当x=28时,y=0.367×282-202.54≈85,且R2=0.802,
所以,二次函数模型中温度解
释了80.2%的产卵数变化。产卵数气温指数函数模型方案3
合作探究对数
方案3解答当x=28oC 时,y ≈44 ,指数回归模型中温度解释了98.5%的产卵数的变化由计算器得:z关于x的线性回归方程
为 对数变换:在 中两边取常用对数得令 ,则
就转换为z=bx+a.相关指数R2=0.98最好的模型是哪个?线性模型二次函数模型指数函数模型比一比最好的模型是哪个?
回归分析(二)则回归方程的残差计算公式分别为:由计算可得:因此模型(1)的拟合效果远远优于模型(2)。
总 结 对于给定的样本点
两个含有未知参数的模型:其中a和b都是未知参数。拟合效果比较的步骤为:
(1)分别建立对应于两个模型的回归方程
与 其中 和 分别是参数a和b的估计值;
(2)分别计算两个回归方程的残差平方和
与
(3)若 则 的效果比
的好;反之, 的效果不如 的好。练习:为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下: (1)用天数作解释变量,繁殖个数作预报变量,作出这些
数据的散点图;
(2) 描述解释变量与预报变量
之间的关系;
(3) 计算残差、相关指数R2.解:(1)散点图如右所示 (2)由散点图看出样本点分布在一条指数函数y= 的周围,于是令Z=lny,则由计数器算得 则有(3)即解释变量天数对预报变量繁殖细菌得个数解释了99.99%.练习 假设关于某设备的使用年限x和所支出的维修费用 y(万元),有如下的统计资料。若由资料知,y对x呈线性相关关系。试求:
(1)线性回归方程 的回归系数 ;
(2)求残差平方和;
(3)求相关系数 ;
(4)估计使用年限为10年时,维修费用是多少?解:(1)由已知数据制成表格。所以有
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题选修2-3——统计案例
引入线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用
利用线性回归模型解决一类非线性回归问题
正确理解分析方法与结果复习回顾2、数据点和它在回归直线上相应位置的差异 是随机误差的效应,称 为残差。3、对每名女大学生计算这个差异,然后分别将所得的值平方后加起来,用数学符号表示为:
称为残差平方和,它代表了随机误差的效应。4、两个指标:
(1)类比样本方差估计总体方差的思想,可以用作
为 的估计量, 越小,预报精度越高。(2)我们可以用相关指数R2来刻画回归的效果,其
计算公式是: R2 ?1,说明回归方程拟合的越好;R2?0,说明回归方程拟合的越差。 在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否线性相关,是否可以用回归模型来拟合数据。5、残差分析与残差图的定义: 然后,我们可以通过残差 来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析。 我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。案例2 一只红铃虫的产卵数y和温度x有关。现收集了7组观测数据列于表中:(1)试建立产卵数y与温度x之间的回归方程;并预测温度为28oC时产卵数目。
(2)你所建立的模型中温度在多大程度上解释了产卵数的变化?
非线性回归问题假设线性回归方程为 :?=bx+a选 模 型由计算器得:线性回归方程为y=19.87x-463.73
相关指数R2=r2≈0.8642=0.7464估计参数
解:选取气温为解释变量x,产卵数
为预报变量y。所以,二次函数模型中温度解释了74.64%的产卵数变化。探索新知方案1分析和预测当x=28时,y =19.87×28-463.73≈ 93一元线性模型奇怪?93>66 ?
模型不好?
方案2问题3合作探究 t=x2二次函数模型
方案2解答平方变换:令t=x2,产卵数y和温度x之间二次函数模型y=bx2+a就转化为产卵数y和温度的平方t之间线性回归模型y=bt+a作散点图,并由计算器得:y和t之间的线性回归方程为y=0.367t-202.543,相关指数R2=0.802将t=x2代入线性回归方程得:
y=0.367x2 -202.543
当x=28时,y=0.367×282-202.54≈85,且R2=0.802,
所以,二次函数模型中温度解
释了80.2%的产卵数变化。产卵数气温指数函数模型方案3
合作探究对数
方案3解答当x=28oC 时,y ≈44 ,指数回归模型中温度解释了98.5%的产卵数的变化由计算器得:z关于x的线性回归方程
为 对数变换:在 中两边取常用对数得令 ,则
就转换为z=bx+a.相关指数R2=0.98最好的模型是哪个?线性模型二次函数模型指数函数模型比一比最好的模型是哪个?
回归分析(二)则回归方程的残差计算公式分别为:由计算可得:因此模型(1)的拟合效果远远优于模型(2)。
总 结 对于给定的样本点
两个含有未知参数的模型:其中a和b都是未知参数。拟合效果比较的步骤为:
(1)分别建立对应于两个模型的回归方程
与 其中 和 分别是参数a和b的估计值;
(2)分别计算两个回归方程的残差平方和
与
(3)若 则 的效果比
的好;反之, 的效果不如 的好。练习:为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下: (1)用天数作解释变量,繁殖个数作预报变量,作出这些
数据的散点图;
(2) 描述解释变量与预报变量
之间的关系;
(3) 计算残差、相关指数R2.解:(1)散点图如右所示 (2)由散点图看出样本点分布在一条指数函数y= 的周围,于是令Z=lny,则由计数器算得 则有(3)即解释变量天数对预报变量繁殖细菌得个数解释了99.99%.练习 假设关于某设备的使用年限x和所支出的维修费用 y(万元),有如下的统计资料。若由资料知,y对x呈线性相关关系。试求:
(1)线性回归方程 的回归系数 ;
(2)求残差平方和;
(3)求相关系数 ;
(4)估计使用年限为10年时,维修费用是多少?解:(1)由已知数据制成表格。所以有
