(苏教版选修2-3)数学:离散型随机变量的方差
文档属性
| 名称 | (苏教版选修2-3)数学:离散型随机变量的方差 |  | |
| 格式 | rar | ||
| 文件大小 | 144.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-27 08:10:00 | ||
图片预览



文档简介
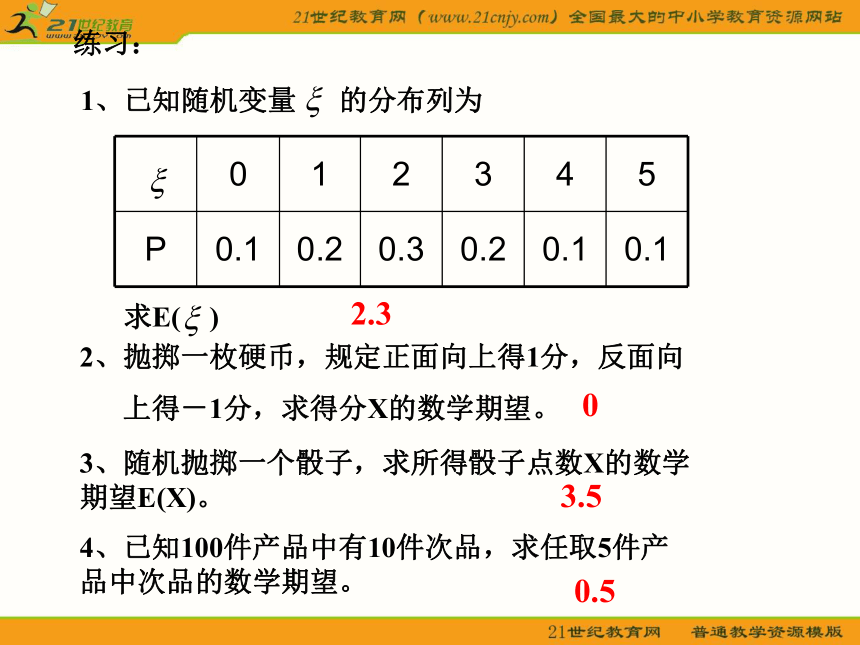
课件11张PPT。离散型随机变量的方差一般地,若离散型随机变量X的概率分布为 则称 E(X)=x1p1+x2p2+…+xnpn为X的均值或数学期望,记为E(X)或μ.其中pi≥0,i=1,2,…,n;p1+p2+…+pn=11、离散型随机变量的均值的定义一、复习若X~H(n,M,N)则E(X)=若X~B(n,p)则E(X)=np2、两个分布的数学期望练习:1、已知随机变量 的分布列为求E( )2、抛掷一枚硬币,规定正面向上得1分,反面向
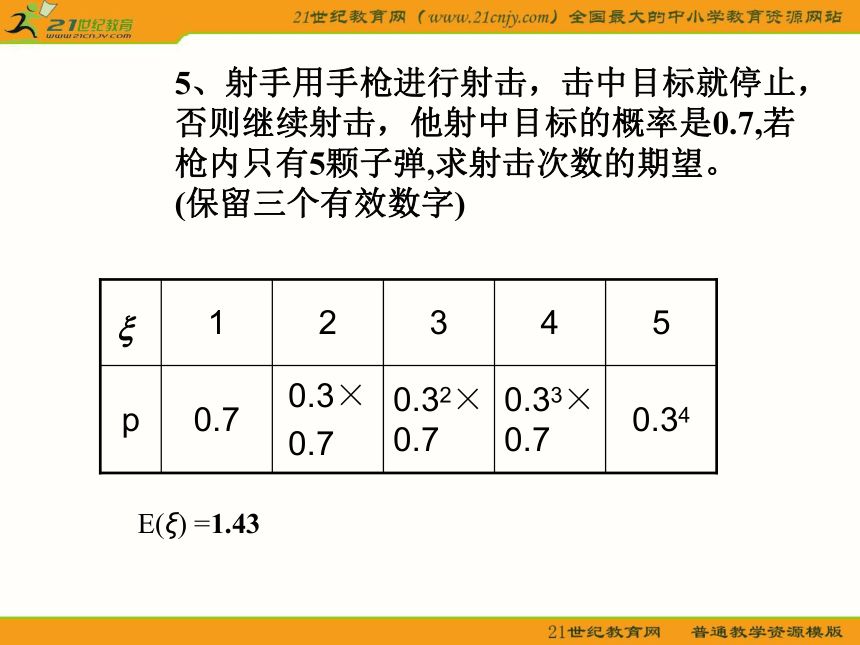
上得-1分,求得分X的数学期望。 2.303、随机抛掷一个骰子,求所得骰子点数X的数学期望E(X)。3.54、已知100件产品中有10件次品,求任取5件产品中次品的数学期望。0.55、射手用手枪进行射击,击中目标就停止,否则继续射击,他射中目标的概率是0.7,若枪内只有5颗子弹,求射击次数的期望。 (保留三个有效数字)E(ξ) =1.43甲、乙两个工人生产同一产品,在相同的条件下,他们生产100件产品所出的不合格品数分别用X1,X2表示, X1,X2的概率分布下:如何比较甲、乙两个工人的技术?E(X1)=0×0.6+1×0.2+2×0.1+3×0.1=0.7E(X2)=0×0.5+1×0.3+2×0.2+3×0=0.7二、离散型随机变量的方差与标准差 对于离散型随机变量X的概率分布如下表,(其中pi≥0,i=1,2,…,n;p1+p2+…+pn=1) 设μ=E(X),则(xi-μ)2描述了xi(i=1,2,...,n)相对于均值μ的偏离程度,故
(x1-μ)2 p1+ (x2-μ)2 p2+...+ (xn-μ)2pn称为离散型随机变量X的方差,记为V(X)或σ2离散型随机变量X的标准差:σ=甲、乙两个工人生产同一产品,在相同的条件下,他们生产100件产品所出的不合格品数分别用X1,X2表示, X1,X2的概率分布下:如何比较甲、乙两个工人的技术?V(X1)=0.6×(0-0.7)2+0.2×(1-0.7)2+0.1×(2-0.7)2+0.1×(3-0.7)2=1.01V(X2)=0.5×(0-0.7)2+0.3×(1-0.7)2+0.2×(2-0.7)2+0×(3-0.7)2=0.61乙的技术稳定性较好例.设随机变量X的分布列为 X 1 2 … n P n1 n1 … n1 求V(X) E(X)= (1+2+...+n)=V(X)= 故 V(X)= V(X)考察0-1分布E(X)=0×(1-p)+1×p=p方差V(X)=(0-p)2(1-p)+(1-p)2×p=p(1-p)标准差σ=若X~H(n,M,N)则V(X)=若X~B(n,p)则V(X)=np(1-p)
上得-1分,求得分X的数学期望。 2.303、随机抛掷一个骰子,求所得骰子点数X的数学期望E(X)。3.54、已知100件产品中有10件次品,求任取5件产品中次品的数学期望。0.55、射手用手枪进行射击,击中目标就停止,否则继续射击,他射中目标的概率是0.7,若枪内只有5颗子弹,求射击次数的期望。 (保留三个有效数字)E(ξ) =1.43甲、乙两个工人生产同一产品,在相同的条件下,他们生产100件产品所出的不合格品数分别用X1,X2表示, X1,X2的概率分布下:如何比较甲、乙两个工人的技术?E(X1)=0×0.6+1×0.2+2×0.1+3×0.1=0.7E(X2)=0×0.5+1×0.3+2×0.2+3×0=0.7二、离散型随机变量的方差与标准差 对于离散型随机变量X的概率分布如下表,(其中pi≥0,i=1,2,…,n;p1+p2+…+pn=1) 设μ=E(X),则(xi-μ)2描述了xi(i=1,2,...,n)相对于均值μ的偏离程度,故
(x1-μ)2 p1+ (x2-μ)2 p2+...+ (xn-μ)2pn称为离散型随机变量X的方差,记为V(X)或σ2离散型随机变量X的标准差:σ=甲、乙两个工人生产同一产品,在相同的条件下,他们生产100件产品所出的不合格品数分别用X1,X2表示, X1,X2的概率分布下:如何比较甲、乙两个工人的技术?V(X1)=0.6×(0-0.7)2+0.2×(1-0.7)2+0.1×(2-0.7)2+0.1×(3-0.7)2=1.01V(X2)=0.5×(0-0.7)2+0.3×(1-0.7)2+0.2×(2-0.7)2+0×(3-0.7)2=0.61乙的技术稳定性较好例.设随机变量X的分布列为 X 1 2 … n P n1 n1 … n1 求V(X) E(X)= (1+2+...+n)=V(X)= 故 V(X)= V(X)考察0-1分布E(X)=0×(1-p)+1×p=p方差V(X)=(0-p)2(1-p)+(1-p)2×p=p(1-p)标准差σ=若X~H(n,M,N)则V(X)=若X~B(n,p)则V(X)=np(1-p)
