(苏教版选修2-3)数学:离散型随机变量的均值
文档属性
| 名称 | (苏教版选修2-3)数学:离散型随机变量的均值 |  | |
| 格式 | rar | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-27 08:10:00 | ||
图片预览




文档简介
课件10张PPT。离散型随机变量的均值1、什么叫n次独立重复试验?一.复习 一般地,由n次试验构成,且每次试验互相独立完成,每次试验的结果仅有两种对立的状态,即A与 ,每次试验中P(A)=p>0。称这样的试验为n次独立重复试验,也称伯努利试验。1).每次试验是在同样的条件下进行的;
2).各次试验中的事件是相互独立的
3).每次试验都只有两种结果:发生与不发生
4).每次试验,某事件发生的概率是相同的.2、什么叫二项分布? 一般地,设离散型随机变量ξ可能取的值为 x1,x2,……,xi,…, ξ取每一个值xi(i=1,2,…)的概率P(ξ=xi)=pi,则称下表为随机变量ξ的概率分布, 由概率的性质可知,任一离散型随机变量的分布列都具有下述两个性质:
(1)pi≥0,i=1,2,…;
(2)p1+p2+…=1.
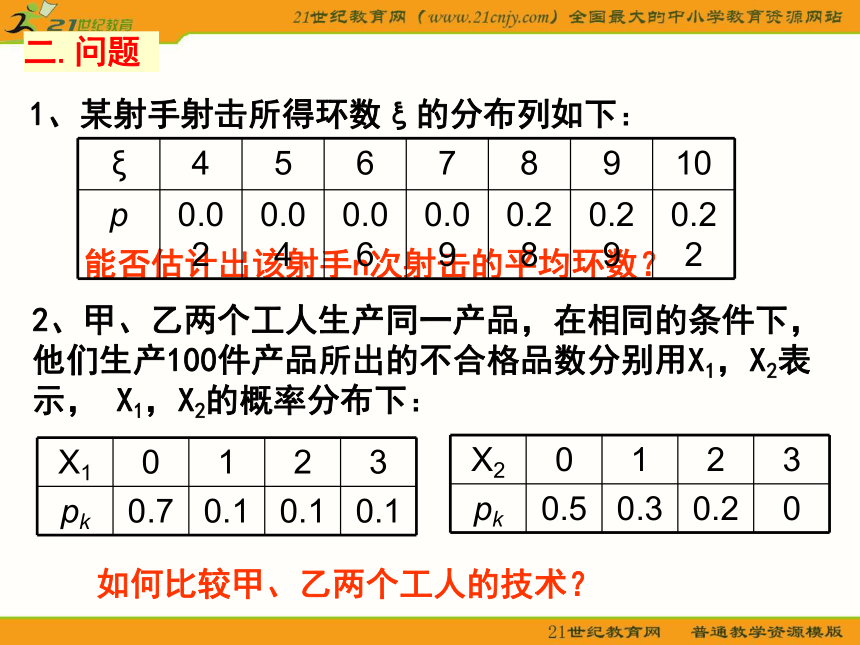
3、离散型随机变量的概率分布1、某射手射击所得环数ξ的分布列如下:能否估计出该射手n次射击的平均环数?二.问题2、甲、乙两个工人生产同一产品,在相同的条件下,他们生产100件产品所出的不合格品数分别用X1,X2表示, X1,X2的概率分布下:如何比较甲、乙两个工人的技术?1、在n次射击之前,虽然不能确定各次射击所得的环数,但可以根据已知的分布列估计n次射击的平均环数.根据这个射手射击所得环数ξ的分布列,他在n次射击中,预计有大约P(ξ=4)×n=0.02n 次得4环,P(ξ=5)×n=0.04n 次得5环,……P(ξ=10)×n=0.22n 次得10环.n次射击的总环数约等于4×0.02×n+5×0.04×n+…+10×0.22×n
=(4×0.02+5×0.04+…+10×0.22)×n,从而,n次射击的平均环数约等于(4×0.02+5×0.04+…+10×0.22)×n÷n=8.32.一般地,若离散型随机变量X的概率分布为 则称 E(X)=x1p1+x2p2+…+xnpn为X的均值或数学期望,记为E(X)或μ.类似地,对任一射手,若已知其射击所得环数X的分布列,即已知各个P(X=i)(i=0,1,2,…,10),则可预计他任意n次射击的平均环数是
E(X)=0×P(X=0)+1×P(X=1)+…+10×P(X=10).我们称E(X)为此射手射击所得环数X的期望,它刻划了随机变量X所取的平均值,从一个方面反映了射手的射击水平.其中pi≥0,i=1,2,…,n;p1+p2+…+pn=1E(X1)=0×0.7+1×0.1+2×0.1+3×0.1=0.6E(X2)=0×0.5+1×0.3+2×0.2+3×0=0.7对于问题2由于E(X1)<E(X2),即甲工人生产出废品数的均值小,从这个意义上讲,甲的技术比乙的技术好。例2 从批量较大的成品中随机取出10件产品进行质量检查,若这批产品的不合格品率为0.05,随机变量X表示这10件产品中的不合格品数,求随机变量X的数学期望E(X).例1 高三(1)班的联欢会上设计了一项游戏,在一个口袋中装有10个红球,20个白球,这些球除颜色外完全相同。某学生一次从中摸出5个球,其中红球的个数为X,求X的数学期望.练习:1、已知随机变量 的分布列为求E( )2、抛掷一枚硬币,规定正面向上得1分,反面向
上得-1分,求得分X的数学期望。 2.303、随机抛掷一个骰子,求所得骰子点数X的数学期望E(X)。3.5考察0-1分布E(X)=0×(1-p)+1×p=p若X~H(n,M,N)则E(X)=若X~B(n,p)则E(X)=np
2).各次试验中的事件是相互独立的
3).每次试验都只有两种结果:发生与不发生
4).每次试验,某事件发生的概率是相同的.2、什么叫二项分布? 一般地,设离散型随机变量ξ可能取的值为 x1,x2,……,xi,…, ξ取每一个值xi(i=1,2,…)的概率P(ξ=xi)=pi,则称下表为随机变量ξ的概率分布, 由概率的性质可知,任一离散型随机变量的分布列都具有下述两个性质:
(1)pi≥0,i=1,2,…;
(2)p1+p2+…=1.
3、离散型随机变量的概率分布1、某射手射击所得环数ξ的分布列如下:能否估计出该射手n次射击的平均环数?二.问题2、甲、乙两个工人生产同一产品,在相同的条件下,他们生产100件产品所出的不合格品数分别用X1,X2表示, X1,X2的概率分布下:如何比较甲、乙两个工人的技术?1、在n次射击之前,虽然不能确定各次射击所得的环数,但可以根据已知的分布列估计n次射击的平均环数.根据这个射手射击所得环数ξ的分布列,他在n次射击中,预计有大约P(ξ=4)×n=0.02n 次得4环,P(ξ=5)×n=0.04n 次得5环,……P(ξ=10)×n=0.22n 次得10环.n次射击的总环数约等于4×0.02×n+5×0.04×n+…+10×0.22×n
=(4×0.02+5×0.04+…+10×0.22)×n,从而,n次射击的平均环数约等于(4×0.02+5×0.04+…+10×0.22)×n÷n=8.32.一般地,若离散型随机变量X的概率分布为 则称 E(X)=x1p1+x2p2+…+xnpn为X的均值或数学期望,记为E(X)或μ.类似地,对任一射手,若已知其射击所得环数X的分布列,即已知各个P(X=i)(i=0,1,2,…,10),则可预计他任意n次射击的平均环数是
E(X)=0×P(X=0)+1×P(X=1)+…+10×P(X=10).我们称E(X)为此射手射击所得环数X的期望,它刻划了随机变量X所取的平均值,从一个方面反映了射手的射击水平.其中pi≥0,i=1,2,…,n;p1+p2+…+pn=1E(X1)=0×0.7+1×0.1+2×0.1+3×0.1=0.6E(X2)=0×0.5+1×0.3+2×0.2+3×0=0.7对于问题2由于E(X1)<E(X2),即甲工人生产出废品数的均值小,从这个意义上讲,甲的技术比乙的技术好。例2 从批量较大的成品中随机取出10件产品进行质量检查,若这批产品的不合格品率为0.05,随机变量X表示这10件产品中的不合格品数,求随机变量X的数学期望E(X).例1 高三(1)班的联欢会上设计了一项游戏,在一个口袋中装有10个红球,20个白球,这些球除颜色外完全相同。某学生一次从中摸出5个球,其中红球的个数为X,求X的数学期望.练习:1、已知随机变量 的分布列为求E( )2、抛掷一枚硬币,规定正面向上得1分,反面向
上得-1分,求得分X的数学期望。 2.303、随机抛掷一个骰子,求所得骰子点数X的数学期望E(X)。3.5考察0-1分布E(X)=0×(1-p)+1×p=p若X~H(n,M,N)则E(X)=若X~B(n,p)则E(X)=np
