新课标A版选修四4-4参数方程学案
文档属性
| 名称 | 新课标A版选修四4-4参数方程学案 |
|
|
| 格式 | rar | ||
| 文件大小 | 52.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-27 16:56:00 | ||
图片预览




文档简介
2.1 参数方程的概念
一、【学习目标】
了解抛物运动轨迹的参数方程及参数的意义,理解参数方程的概念。
二、【创设情境】
1.探究:
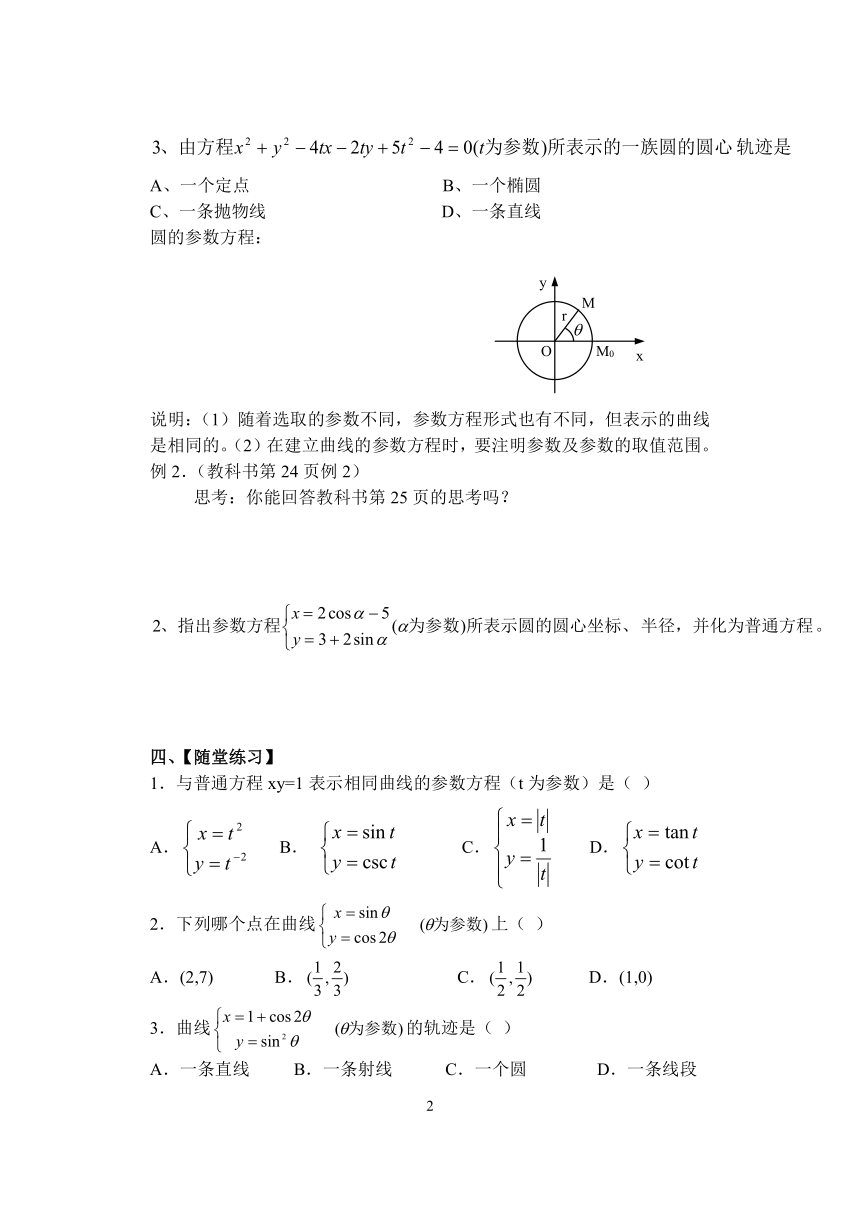
(1)平抛运动:
练习:斜抛运动:
三、【新知探究】
参数方程的概念:(见教科书第22页)
说明:(1)一般来说,参数的变化范围是有限制的。
(2)参数是联系变量x,y的桥梁,可以有实际意义,也可无实际意义。
例1.(教科书第22页例1)已知曲线C的参数方程是 (t为参数)
(1)判断点M1(0,1),M2(5,4)与曲线C的位置关系;
(2)已知点M3(6,a)在曲线C上,求a的值。
A、一个定点 B、一个椭圆
C、一条抛物线 D、一条直线
圆的参数方程:
说明:(1)随着选取的参数不同,参数方程形式也有不同,但表示的曲线是相同的。(2)在建立曲线的参数方程时,要注明参数及参数的取值范围。
例2.(教科书第24页例2)
思考:你能回答教科书第25页的思考吗?
四、【随堂练习】
1.与普通方程xy=1表示相同曲线的参数方程(t为参数)是( )
A. B. C. D.
2.下列哪个点在曲线上( )
A.(2,7) B. C. D.(1,0)
3.曲线的轨迹是( )
A.一条直线 B.一条射线 C.一个圆 D.一条线段
2.2圆的参数方程及应用
一、【学习目标】
利用圆的几何性质求最值(数形结合)
能选取适当的参数,求圆的参数方程
二、【例题精讲】
(一)、最值问题
1.已知P(x,y)圆C:x2+y2-6x-4y+12=0上的点。
(1)求 的最小值与最大值
(2)求x-y的最大值与最小值
2.圆x2+y2=1上的点到直线3x+4y-25=0的距离最小值是 ;
3圆(x-1)2+(y+2)2=4上的点到直线2x-y+1=0的最短距离是_______;
4 过点(2,1)的直线中,被圆x2+y2-2x+4y=0截得的弦:
为最长的直线方程是_________;为最短的直线方程是__________;
5若实数x,y满足x2+y2-2x+4y=0,则x-2y的最大值为 ;
(二)、参数法求轨迹
1)一动点在圆x2+y2=1上移动,求它与定点(3,0)连线的中点的轨迹方程
2)已知点A(2,0),P是x2+y2=1上任一点,的平分线交PA于Q点,求Q点的轨迹.
解题思想:将要求点的坐标x,y分别用同一个参数来表示
例题:1)点P(m,n)在圆x2+y2=1上运动,求点Q(m+n,2mn)的轨迹方程
2)方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0.若该方
程表示一个圆,求m的取值范围和圆心的轨迹方程。
三【课堂小结】
小结:本节学习内容要求掌握
1.用圆的参数方程求最值;
2.用参数法求轨迹方程,消参。
2.3圆锥曲线的参数方程
一、【学习目标】
了解圆锥曲线的参数方程及参数的意义
能选取适当的参数,求简单曲线的参数方程
二、【复习引入】
1.写出圆方程的标准式和对应的参数方程。
2.写出椭圆、双曲线和抛物线的标准方程。
3.能模仿圆参数方程的推导,写出圆锥曲线的参数方程吗?
三、【新知探究】
1.椭圆的推导:椭圆参数方程:
2.双曲线的参数方程:双曲线参数方程:
3.抛物线的参数方程:抛物线参数方程:
关于参数几点说明:
(1) 参数方程中参数可以是有物理意义,几何意义,也可以没有明显意义。
(1) 同一曲线选取的参数不同,曲线的参数方程形式也不一样
(1) 在实际问题中要确定参数的取值范围
参数方程的意义:
参数方程是曲线点的位置的另一种表示形式,它借助于中间变量把曲线上的动点的两个坐标间接地联系起来,参数方程与变通方程同等地描述,了解曲线,参数方程实际上是一个方程组,其中,分别为曲线上点M的横坐标和纵坐标。
1、 参数方程求法
1、 关于参数方程中参数的选取
四、【例题精讲】
例1.设炮弹发射角为,发射速度为,
(1)求子弹弹道曲线的参数方程(不计空气阻力)
(2)若,,当炮弹发出2秒时,
1 求炮弹高度
1 求出炮弹的射程
例2.求椭圆的参数方程(见教材P.40)
椭圆参数方程 (为参数)
变式训练1. 已知椭圆 (为参数)
求 (1)时对应的点P的坐标
(2)直线OP的倾斜角
变式训练2 A点椭圆长轴一个端点,若椭圆上存在一点P,使∠OPA=90°,其中O为椭圆中心,求椭圆离心率的取值范围。
例3.把圆化为参数方程
(1) 用圆上任一点过原点的弦和轴正半轴夹角为参数
(1) 用圆中过原点的弦长为参数
2.4圆锥曲线参数方程的应用
一、【学习目标】
利用圆锥曲线的参数方程来确定最值,解决有关点的轨迹问题
选择适当的参数方程求最值。
二、【复习引入】
通过参数简明地表示曲线上任一点坐标将解析几何中以计算问题化为三角问题,从而运用三角性质及变换公式帮助求解诸如最值,参数取值范围等问题。
三、【新知探究】
例1.求椭圆的内接矩形面积的最大值
变式训练1
椭圆 ()与轴正向交于点A,若这个椭圆上存在点P,使OP⊥AP,(O为原点),求离心率的范围。
例2.AB为过椭圆中心的弦,, 为焦点,求△ABF1面积的最大值。
例3.抛物线的内接三角形的一个顶点在原点,其重心恰是抛物线的焦点,求内接三角形的周长。
例4
例5 、过P(0,1)到双曲线最小距离
变式训练2:
设P为等轴双曲线上的一点,,为两个焦点,证明
例5,在抛物线的顶点,引两互相垂直的两条弦OA,OB,求顶点O在AB上射影H的轨迹方程。
三、巩固与练习
四、小 结:本节课学习了以下内容:
适当使用参数表示已知曲线上的点用以求最值问题
五、课后作业:
2.5直线的参数方程
一、【学习目标】
了解直线参数方程的条件及参数的意义
能根据直线的几何条件,写出直线的参数方程及参数的意义
二、【复习引入】
1.写出圆方程的标准式和对应的参数方程。
2.写出椭圆参数方程.
3.复习方向向量的概念.提出问题:已知直线的一个点和倾斜角,如何表示直线的参数方程
三、【新知探究】
1、 教师引导学生推导直线的参数方程:
过定点倾斜角为的直线的参数方程
1、 辨析直线的参数方程:
T的几何意义是指它表示点P0P的长,带符号.
直线的参数方程应用:课本例题,此略.
四、【课堂小结】
(1)直线参数方程求法
(2)直线参数方程的特点
(3)根据已知条件和图形的几何性质,注意参数的意义
五、作业:课本P39习题2.3
2.6参数方程与普通方程互化
一、【学习目标】
掌握参数方程化为普通方程几种基本方法
选取适当的参数化普通方程为参数方程
二、【复习引入】
(1)圆的参数方程
(2)椭圆的参数方程
三、【新知探究】
1、参数方程化为普通方程的过程就是消参过程常见方法有三种:
(1) 代入法:利用解方程的技巧求出参数t,然后代入消去参数
(2) 三角法:利用三角恒等式消去参数
(3) 整体消元法:根据参数方程本身的结构特征,从整体上消去。
化参数方程为普通方程为:在消参过程中注意变量、取值范围的一致性,必须根据参数的取值范围,确定和值域得、的取值范围。
2、常见曲线的参数方程
四、【例题精讲】
将下列参数方程化为普通方程
(1) (2)
(3) (4) (5)
变式训练1
(1)方程 表示的曲线
A、一条直线 B、两条射线 C、一条线段 D、抛物线的一部分
(2)下列方程中,当方程表示同一曲线的点
A、 B、 C、 D、
例2化下列曲线的参数方程为普通方程,并指出它是什么曲线。
(1) (t是参数) (2) (是参数)
(3) (t是参数)
变式训练2:P是双曲线 (t是参数)上任一点,,是该焦点,求△F1F2的重心G的轨迹的普通方程。
例3、已知圆O半径为1,P是圆上动点,Q(4,0)是轴上的定点,M是PQ的中点,当点P绕O作匀速圆周运动时,求点M的轨迹的参数方程。
变式训练3:
已知为圆上任意一点,求的最大值和最小值。
五、课后作业:见教材53页 2.3.4.5
2.7圆的渐开线与摆线
一、【学习目标】
了解圆的渐开线的参数方程, 了解摆线的生成过程及它的参数方程.
学习用向量知识推导运动轨迹曲线的方法和步骤
二、【复习引入】
1 复习:圆的参数方程
四、【新知探究】
1、以基圆圆心O为原点,直线OA为x轴,建立平面直角坐标系,可得圆渐开线的参数方程为
2、在研究平摆线的参数方程中,取定直线为轴,定点M滚动时落在直线上的一个位置为原点,建立直角坐标系,设圆的半径为r,可得摆线的参数方程为。
例1 求半径为4的圆的渐开线参数方程
变式训练1 当,时,求圆渐开线 上对应点A、B坐标并求出A、B间的距离。
变式训练2 求圆的渐开线上当对应的点的直角坐标。
例2 求半径为2的圆的摆线的参数方程
变式训练3
求摆线 与直线的交点的直角坐标
例3、设圆的半径为8,沿轴正向滚动,开始时圆与轴相切于原点O,记圆上动点为M它随圆的滚动而改变位置,写出圆滚动一周时M点的轨迹方程,画出相应曲线,求此曲线上纵坐标的最大值,说明该曲线的对称轴。
三、巩固与练习
四、小 结:.
五、课后作业:见教材P.57/16
x
y
O
v=v0
v=100m/s
A
O
500
y
x
x
y
O
r
M
M0
x
1
一、【学习目标】
了解抛物运动轨迹的参数方程及参数的意义,理解参数方程的概念。
二、【创设情境】
1.探究:
(1)平抛运动:
练习:斜抛运动:
三、【新知探究】
参数方程的概念:(见教科书第22页)
说明:(1)一般来说,参数的变化范围是有限制的。
(2)参数是联系变量x,y的桥梁,可以有实际意义,也可无实际意义。
例1.(教科书第22页例1)已知曲线C的参数方程是 (t为参数)
(1)判断点M1(0,1),M2(5,4)与曲线C的位置关系;
(2)已知点M3(6,a)在曲线C上,求a的值。
A、一个定点 B、一个椭圆
C、一条抛物线 D、一条直线
圆的参数方程:
说明:(1)随着选取的参数不同,参数方程形式也有不同,但表示的曲线是相同的。(2)在建立曲线的参数方程时,要注明参数及参数的取值范围。
例2.(教科书第24页例2)
思考:你能回答教科书第25页的思考吗?
四、【随堂练习】
1.与普通方程xy=1表示相同曲线的参数方程(t为参数)是( )
A. B. C. D.
2.下列哪个点在曲线上( )
A.(2,7) B. C. D.(1,0)
3.曲线的轨迹是( )
A.一条直线 B.一条射线 C.一个圆 D.一条线段
2.2圆的参数方程及应用
一、【学习目标】
利用圆的几何性质求最值(数形结合)
能选取适当的参数,求圆的参数方程
二、【例题精讲】
(一)、最值问题
1.已知P(x,y)圆C:x2+y2-6x-4y+12=0上的点。
(1)求 的最小值与最大值
(2)求x-y的最大值与最小值
2.圆x2+y2=1上的点到直线3x+4y-25=0的距离最小值是 ;
3圆(x-1)2+(y+2)2=4上的点到直线2x-y+1=0的最短距离是_______;
4 过点(2,1)的直线中,被圆x2+y2-2x+4y=0截得的弦:
为最长的直线方程是_________;为最短的直线方程是__________;
5若实数x,y满足x2+y2-2x+4y=0,则x-2y的最大值为 ;
(二)、参数法求轨迹
1)一动点在圆x2+y2=1上移动,求它与定点(3,0)连线的中点的轨迹方程
2)已知点A(2,0),P是x2+y2=1上任一点,的平分线交PA于Q点,求Q点的轨迹.
解题思想:将要求点的坐标x,y分别用同一个参数来表示
例题:1)点P(m,n)在圆x2+y2=1上运动,求点Q(m+n,2mn)的轨迹方程
2)方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0.若该方
程表示一个圆,求m的取值范围和圆心的轨迹方程。
三【课堂小结】
小结:本节学习内容要求掌握
1.用圆的参数方程求最值;
2.用参数法求轨迹方程,消参。
2.3圆锥曲线的参数方程
一、【学习目标】
了解圆锥曲线的参数方程及参数的意义
能选取适当的参数,求简单曲线的参数方程
二、【复习引入】
1.写出圆方程的标准式和对应的参数方程。
2.写出椭圆、双曲线和抛物线的标准方程。
3.能模仿圆参数方程的推导,写出圆锥曲线的参数方程吗?
三、【新知探究】
1.椭圆的推导:椭圆参数方程:
2.双曲线的参数方程:双曲线参数方程:
3.抛物线的参数方程:抛物线参数方程:
关于参数几点说明:
(1) 参数方程中参数可以是有物理意义,几何意义,也可以没有明显意义。
(1) 同一曲线选取的参数不同,曲线的参数方程形式也不一样
(1) 在实际问题中要确定参数的取值范围
参数方程的意义:
参数方程是曲线点的位置的另一种表示形式,它借助于中间变量把曲线上的动点的两个坐标间接地联系起来,参数方程与变通方程同等地描述,了解曲线,参数方程实际上是一个方程组,其中,分别为曲线上点M的横坐标和纵坐标。
1、 参数方程求法
1、 关于参数方程中参数的选取
四、【例题精讲】
例1.设炮弹发射角为,发射速度为,
(1)求子弹弹道曲线的参数方程(不计空气阻力)
(2)若,,当炮弹发出2秒时,
1 求炮弹高度
1 求出炮弹的射程
例2.求椭圆的参数方程(见教材P.40)
椭圆参数方程 (为参数)
变式训练1. 已知椭圆 (为参数)
求 (1)时对应的点P的坐标
(2)直线OP的倾斜角
变式训练2 A点椭圆长轴一个端点,若椭圆上存在一点P,使∠OPA=90°,其中O为椭圆中心,求椭圆离心率的取值范围。
例3.把圆化为参数方程
(1) 用圆上任一点过原点的弦和轴正半轴夹角为参数
(1) 用圆中过原点的弦长为参数
2.4圆锥曲线参数方程的应用
一、【学习目标】
利用圆锥曲线的参数方程来确定最值,解决有关点的轨迹问题
选择适当的参数方程求最值。
二、【复习引入】
通过参数简明地表示曲线上任一点坐标将解析几何中以计算问题化为三角问题,从而运用三角性质及变换公式帮助求解诸如最值,参数取值范围等问题。
三、【新知探究】
例1.求椭圆的内接矩形面积的最大值
变式训练1
椭圆 ()与轴正向交于点A,若这个椭圆上存在点P,使OP⊥AP,(O为原点),求离心率的范围。
例2.AB为过椭圆中心的弦,, 为焦点,求△ABF1面积的最大值。
例3.抛物线的内接三角形的一个顶点在原点,其重心恰是抛物线的焦点,求内接三角形的周长。
例4
例5 、过P(0,1)到双曲线最小距离
变式训练2:
设P为等轴双曲线上的一点,,为两个焦点,证明
例5,在抛物线的顶点,引两互相垂直的两条弦OA,OB,求顶点O在AB上射影H的轨迹方程。
三、巩固与练习
四、小 结:本节课学习了以下内容:
适当使用参数表示已知曲线上的点用以求最值问题
五、课后作业:
2.5直线的参数方程
一、【学习目标】
了解直线参数方程的条件及参数的意义
能根据直线的几何条件,写出直线的参数方程及参数的意义
二、【复习引入】
1.写出圆方程的标准式和对应的参数方程。
2.写出椭圆参数方程.
3.复习方向向量的概念.提出问题:已知直线的一个点和倾斜角,如何表示直线的参数方程
三、【新知探究】
1、 教师引导学生推导直线的参数方程:
过定点倾斜角为的直线的参数方程
1、 辨析直线的参数方程:
T的几何意义是指它表示点P0P的长,带符号.
直线的参数方程应用:课本例题,此略.
四、【课堂小结】
(1)直线参数方程求法
(2)直线参数方程的特点
(3)根据已知条件和图形的几何性质,注意参数的意义
五、作业:课本P39习题2.3
2.6参数方程与普通方程互化
一、【学习目标】
掌握参数方程化为普通方程几种基本方法
选取适当的参数化普通方程为参数方程
二、【复习引入】
(1)圆的参数方程
(2)椭圆的参数方程
三、【新知探究】
1、参数方程化为普通方程的过程就是消参过程常见方法有三种:
(1) 代入法:利用解方程的技巧求出参数t,然后代入消去参数
(2) 三角法:利用三角恒等式消去参数
(3) 整体消元法:根据参数方程本身的结构特征,从整体上消去。
化参数方程为普通方程为:在消参过程中注意变量、取值范围的一致性,必须根据参数的取值范围,确定和值域得、的取值范围。
2、常见曲线的参数方程
四、【例题精讲】
将下列参数方程化为普通方程
(1) (2)
(3) (4) (5)
变式训练1
(1)方程 表示的曲线
A、一条直线 B、两条射线 C、一条线段 D、抛物线的一部分
(2)下列方程中,当方程表示同一曲线的点
A、 B、 C、 D、
例2化下列曲线的参数方程为普通方程,并指出它是什么曲线。
(1) (t是参数) (2) (是参数)
(3) (t是参数)
变式训练2:P是双曲线 (t是参数)上任一点,,是该焦点,求△F1F2的重心G的轨迹的普通方程。
例3、已知圆O半径为1,P是圆上动点,Q(4,0)是轴上的定点,M是PQ的中点,当点P绕O作匀速圆周运动时,求点M的轨迹的参数方程。
变式训练3:
已知为圆上任意一点,求的最大值和最小值。
五、课后作业:见教材53页 2.3.4.5
2.7圆的渐开线与摆线
一、【学习目标】
了解圆的渐开线的参数方程, 了解摆线的生成过程及它的参数方程.
学习用向量知识推导运动轨迹曲线的方法和步骤
二、【复习引入】
1 复习:圆的参数方程
四、【新知探究】
1、以基圆圆心O为原点,直线OA为x轴,建立平面直角坐标系,可得圆渐开线的参数方程为
2、在研究平摆线的参数方程中,取定直线为轴,定点M滚动时落在直线上的一个位置为原点,建立直角坐标系,设圆的半径为r,可得摆线的参数方程为。
例1 求半径为4的圆的渐开线参数方程
变式训练1 当,时,求圆渐开线 上对应点A、B坐标并求出A、B间的距离。
变式训练2 求圆的渐开线上当对应的点的直角坐标。
例2 求半径为2的圆的摆线的参数方程
变式训练3
求摆线 与直线的交点的直角坐标
例3、设圆的半径为8,沿轴正向滚动,开始时圆与轴相切于原点O,记圆上动点为M它随圆的滚动而改变位置,写出圆滚动一周时M点的轨迹方程,画出相应曲线,求此曲线上纵坐标的最大值,说明该曲线的对称轴。
三、巩固与练习
四、小 结:.
五、课后作业:见教材P.57/16
x
y
O
v=v0
v=100m/s
A
O
500
y
x
x
y
O
r
M
M0
x
1
