第24章圆24.1.1---24.1.3复习学案
文档属性
| 名称 | 第24章圆24.1.1---24.1.3复习学案 |
|
|
| 格式 | rar | ||
| 文件大小 | 39.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-28 11:18:00 | ||
图片预览

文档简介
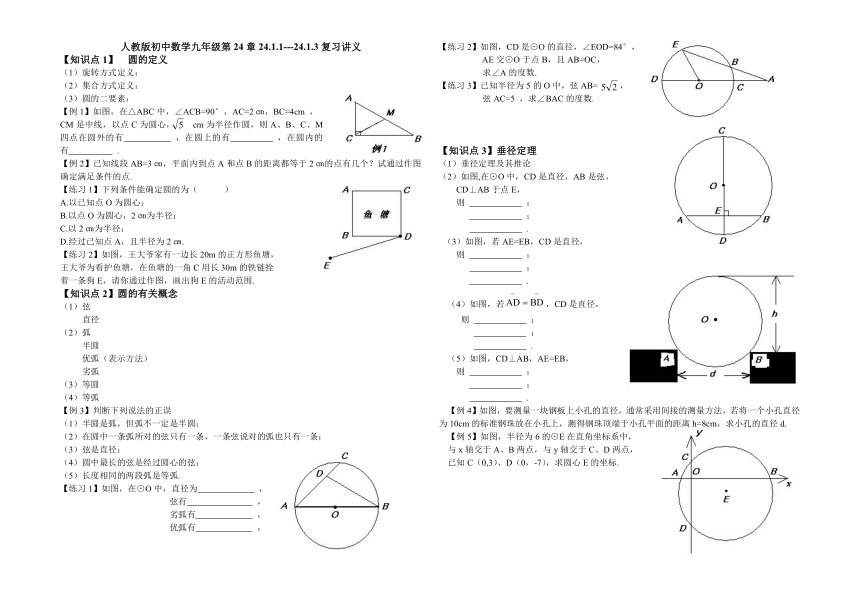
人教版初中数学九年级第24章24.1.1---24.1.3复习讲义
【知识点1】 圆的定义
旋转方式定义:
集合方式定义:
圆的二要素:
【例1】如图,在△ABC中,∠ACB=90°,AC=2㎝,BC=4cm ,
CM是中线,以点C为圆心, cm为半径作圆,则A、B、C、M四点在圆外的有 ,在圆上的有 ,在圆内的有 .
【例2】已知线段AB=3㎝,平面内到点A和点B的距离都等于2㎝的点有几个?试通过作图确定满足条件的点.
【练习1】下列条件能确定圆的为( )
以已知点O为圆心;
以点O为圆心,2㎝为半径;
以2㎝为半径;
经过已知点A,且半径为2㎝.
【练习2】如图,王大爷家有一边长20m的正方形鱼塘,
王大爷为看护鱼塘,在鱼塘的一角C用长30m的铁链拴
着一条狗E,请你通过作图,画出狗E的活动范围.
【知识点2】圆的有关概念
弦
直径
弧
半圆
优弧(表示方法)
劣弧
等圆
等弧
【例3】判断下列说法的正误
半圆是弧,但弧不一定是半圆;
在圆中一条弧所对的弦只有一条,一条弦说对的弧也只有一条;
弦是直径;
圆中最长的弦是经过圆心的弦;
长度相同的两段弧是等弧.
【练习1】如图,在⊙O中,直径为 ,
弦有 ,
劣弧有 ,
优弧有 ,
【练习2】如图,CD是⊙O的直径,∠EOD=84°,
AE交⊙O于点B,且AB=OC,
求∠A的度数.
【练习3】已知半径为5的O中,弦AB= ,
弦AC=5 ,求∠BAC的度数.
【知识点3】垂径定理
垂径定理及其推论
如图,在⊙O中,CD是直径,AB是弦,
CD⊥AB于点E,
则 ;
;
.
(3)如图,若AE=EB,CD是直径,
则 ;
;
.
(4)如图,若,CD是直径,
则 ;
;
.
如图,CD⊥AB,AE=EB,
则 ;
;
.
【例4】如图,要测量一块钢板上小孔的直径,通常采用间接的测量方法,若将一个小孔直径为10cm的标准钢珠放在小孔上,测得钢珠顶端于小孔平面的距离h=8cm,求小孔的直径d.
【例5】如图,半径为6的⊙E在直角坐标系中,
与x轴交于A、B两点,与y轴交于C、D两点,
已知C(0,3)、D(0,-7),求圆心E的坐标.
【练习1】如图,AB是⊙O的弦,OC⊥AB于点C,已知AB=8cm,OC=3cm,
则⊙O的半径为 .
【练习2】如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,
则弦AB的长度为_________ .
【练习3】如图是一个圆弧形门,圆弧所在圆的圆心的高度与该圆的半径相同,AB=CD=20cm,
BD=200cm,且AB、CD于水平面都是垂直的,根据以上数据请计算这个圆弧形门
的最高点离地面的高度.
【知识点4】圆心角、弧、弦、弦心距之间的关系
圆心角的定义
圆心角、弧、弦、弦心距之间的关系
如图,AB、CD是⊙O的两条弦,OE⊥AB,OF⊥CD.
①若AB=CD,则__________, ②若∠AOB=∠COD则__________,
__________, __________,
__________, __________,
③若 ,则__________, ④若OE=OF,则__________,
__________, __________,
__________, __________,
(3)一条弧的度数等于它所对圆心角的度数.
【例6】如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,
CA的长为半径的圆交AB于点D,求的度数.
【例7】如图,在⊙O中,AB为直径,弦DE与AB相交于点C,
且CD=CO.若的度数为30°,求的度数.
【例8】如图,AB、CD是⊙O的两条直径CE∥AB.
求证:
【例9】如图,P为⊙O外一点,PB、PD分别交O于
A、B、C、D四点,PO平分∠BPD。
试说明∠AOB=∠COD
【例10】如图,已知OA、OB是⊙O的半径,C为弧AB的
中点,M、N分别为OA、OB的中点.
求证:MC=NC
【练习1】如图,AB是⊙O的直径,AC∥OD,若 = 70° 求 的度数.
【练习2】如图,在△ABC中,AB=AC,以AB为直径的半圆交BC于点D,交AC于
点E,若弧DE的度数为40°,求A的度数.
【练习3】如图,已知在⊙O中,∠AOD=∠COB ,求证:AB=CD
【练习4】如图,BC是⊙O的直径,OA是⊙O的半径,弦BE∥OA,求证:
【知识点1】 圆的定义
旋转方式定义:
集合方式定义:
圆的二要素:
【例1】如图,在△ABC中,∠ACB=90°,AC=2㎝,BC=4cm ,
CM是中线,以点C为圆心, cm为半径作圆,则A、B、C、M四点在圆外的有 ,在圆上的有 ,在圆内的有 .
【例2】已知线段AB=3㎝,平面内到点A和点B的距离都等于2㎝的点有几个?试通过作图确定满足条件的点.
【练习1】下列条件能确定圆的为( )
以已知点O为圆心;
以点O为圆心,2㎝为半径;
以2㎝为半径;
经过已知点A,且半径为2㎝.
【练习2】如图,王大爷家有一边长20m的正方形鱼塘,
王大爷为看护鱼塘,在鱼塘的一角C用长30m的铁链拴
着一条狗E,请你通过作图,画出狗E的活动范围.
【知识点2】圆的有关概念
弦
直径
弧
半圆
优弧(表示方法)
劣弧
等圆
等弧
【例3】判断下列说法的正误
半圆是弧,但弧不一定是半圆;
在圆中一条弧所对的弦只有一条,一条弦说对的弧也只有一条;
弦是直径;
圆中最长的弦是经过圆心的弦;
长度相同的两段弧是等弧.
【练习1】如图,在⊙O中,直径为 ,
弦有 ,
劣弧有 ,
优弧有 ,
【练习2】如图,CD是⊙O的直径,∠EOD=84°,
AE交⊙O于点B,且AB=OC,
求∠A的度数.
【练习3】已知半径为5的O中,弦AB= ,
弦AC=5 ,求∠BAC的度数.
【知识点3】垂径定理
垂径定理及其推论
如图,在⊙O中,CD是直径,AB是弦,
CD⊥AB于点E,
则 ;
;
.
(3)如图,若AE=EB,CD是直径,
则 ;
;
.
(4)如图,若,CD是直径,
则 ;
;
.
如图,CD⊥AB,AE=EB,
则 ;
;
.
【例4】如图,要测量一块钢板上小孔的直径,通常采用间接的测量方法,若将一个小孔直径为10cm的标准钢珠放在小孔上,测得钢珠顶端于小孔平面的距离h=8cm,求小孔的直径d.
【例5】如图,半径为6的⊙E在直角坐标系中,
与x轴交于A、B两点,与y轴交于C、D两点,
已知C(0,3)、D(0,-7),求圆心E的坐标.
【练习1】如图,AB是⊙O的弦,OC⊥AB于点C,已知AB=8cm,OC=3cm,
则⊙O的半径为 .
【练习2】如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,
则弦AB的长度为_________ .
【练习3】如图是一个圆弧形门,圆弧所在圆的圆心的高度与该圆的半径相同,AB=CD=20cm,
BD=200cm,且AB、CD于水平面都是垂直的,根据以上数据请计算这个圆弧形门
的最高点离地面的高度.
【知识点4】圆心角、弧、弦、弦心距之间的关系
圆心角的定义
圆心角、弧、弦、弦心距之间的关系
如图,AB、CD是⊙O的两条弦,OE⊥AB,OF⊥CD.
①若AB=CD,则__________, ②若∠AOB=∠COD则__________,
__________, __________,
__________, __________,
③若 ,则__________, ④若OE=OF,则__________,
__________, __________,
__________, __________,
(3)一条弧的度数等于它所对圆心角的度数.
【例6】如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,
CA的长为半径的圆交AB于点D,求的度数.
【例7】如图,在⊙O中,AB为直径,弦DE与AB相交于点C,
且CD=CO.若的度数为30°,求的度数.
【例8】如图,AB、CD是⊙O的两条直径CE∥AB.
求证:
【例9】如图,P为⊙O外一点,PB、PD分别交O于
A、B、C、D四点,PO平分∠BPD。
试说明∠AOB=∠COD
【例10】如图,已知OA、OB是⊙O的半径,C为弧AB的
中点,M、N分别为OA、OB的中点.
求证:MC=NC
【练习1】如图,AB是⊙O的直径,AC∥OD,若 = 70° 求 的度数.
【练习2】如图,在△ABC中,AB=AC,以AB为直径的半圆交BC于点D,交AC于
点E,若弧DE的度数为40°,求A的度数.
【练习3】如图,已知在⊙O中,∠AOD=∠COB ,求证:AB=CD
【练习4】如图,BC是⊙O的直径,OA是⊙O的半径,弦BE∥OA,求证:
同课章节目录
