对数函数及其性质

课件38张PPT。学点一学点二学点三学点四学点五学点六学点七学点八1.对数函数的概念
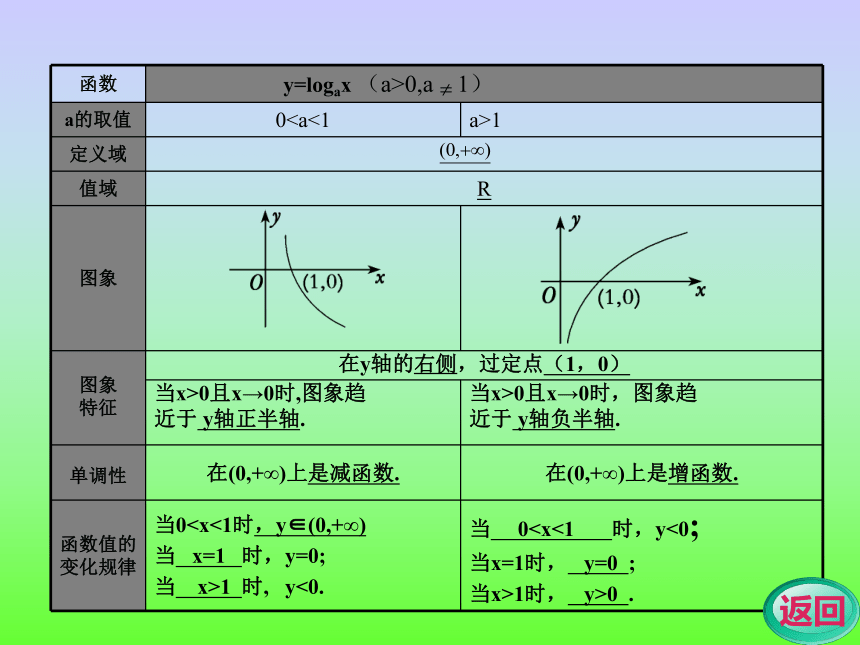
函数 叫做对数函数.
2.对数函数的图象和性质. 图在下一页y=logax(a>0,且a≠1)3.对数函数y=logax(a>0,且a≠1)与指数函数y=ax(a>0,且a≠1)互为 .它们的图象关于 对称.反函数y=x学点一 比较大小比较大小：
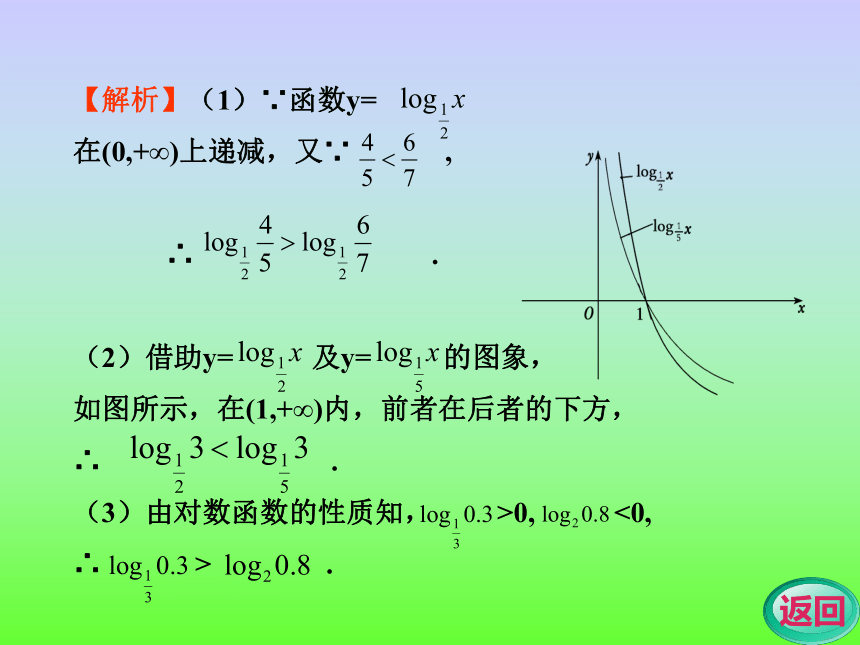
（1） ， ；
（2） , ;
（3） , .【分析】从对数函数单调性及图象变化规律入手.【解析】（1）∵函数y=
在(0,+∞)上递减，又∵ ,
∴ .
（2）借助y= 及y= 的图象，
如图所示，在(1,+∞)内，前者在后者的下方，
∴ .
（3）由对数函数的性质知， >0, <0,
∴ > .【评析】比较两个对数值的大小，常用方法：
（1）当底数相同，真数不同时，用函数的单调性来比较；
（2）当底数不同而真数相同时，常借助图象比较，也可用换底公式转化为同底数的对数后比较；
（3）当底数与真数都不同时，需寻求中间值比较.比较下列各组数中两个值的大小：
（1） ;
（2） ;
（3） (a>0，且a≠1).
（1）考查对数函数y=log2x，因为它的底数2>1,所以它在(0,+∞)上是增函数，于是log23.4（2）考查对数函数y=log0.3x，因为它的底数满足0<0.3<1,所以它在(0,+∞)上是减函数，于是log0.31.8>log0.32.7.
（3）对数函数的增减性决定于对数的底数是大于1还是小于1，而已知条件中并未明确指出底数a与1哪个大，因此，要对底数a进行讨论：
当a>1时，函数y=logax在(0,+∞)上是增函数，于是loga5.1当0loga5.9.求下列函数的定义域：
（1） y= ;
（2） .
【解析】(1)要使函数有意义，必须且只需
x>0 x>0
log0.8x-1≥0 即 x≤0.8
2x-1≠0, x≠ ,
∴0因此，函数的定义域是 .学点二 求定义域【分析】注意考虑问题要全面，切忌丢三落四.（2）要使函数有意义，必须且满足
2x+3>0 x>
x-1>0 解得 x>1
3x-1>0 x>
3x-1 0 x
因此，函数的定义域为 (1,+∞) .【评析】求函数定义域实质上就是据题意列出函数成立的不等式（组）并解之，对于含有对数式的函数定义域的求解，必须同时考虑底数和真数的取值条件，在本例（2）（4）中还用到指数、对数的单调性.求下列函数的定义域：
（1）
（2）
（1）由log0.5(4x-3)≥0
4x-3>0得0<4x-3≤1,
∴ ∴函数的定义域是 .(2)由 16-4x>0 x<2
x+1>0 得 x>-1
x+1≠1 x≠0.
∴-1∴函数的定义域是(-1,0)∪(0,2).学点三 求值域求下列函数的值域：
（1）
（2）
（3）y=loga(a-ax)(a>1).【分析】复合函数的值域问题，要先求函数的定义域，再由单调性求解.【解析】（1）∵-x2-4x+12=-(x2+4x)+12
=-(x+2)2+16≤16,
又∵-x2-4x+12>0, ∴0<-x2-4x+12≤16.
∵y=log x在(0,16］上是减函数,
∴y≥log 16=-4. ∴函数的值域为［-4,+∞).
（2）∵x2-2x-3=(x-1)2-4≥-4,
又∵x2-2x-3>0,且y=log x在(0,+∞)上是减函数,
∴y∈R,
∴函数的值域为实数集R.（3）令u=a-ax,
∵u>0,a>1,∴ax∴y=loga(a-ax)的定义域为{x|x<1},
∵ax0,u=a-ax∴y=loga(a-ax)∴函数的值域为{y|y<1}.【评析】求函数的值域一定要注意定义域对它的影响，然后利用函数的单调性求之，当函数中含有参数时，有时需要讨论参数的取值.求值域：
（1）y=log2(x2-4x+6); （2） .(1)∵x2-4x+6=(x-2)2+2≥2,又∵y=log2x在(0,+∞)上是增函数,
∴log2(x2-4x+6)≥log22=1.
∴函数的值域是［1,+∞).
(2) ∵-x2+2x+2=-(x-1)2+3≤3,
∴ <0或 ≥ .
∴ ≥
∴函数的值域是 , 学点三 对数函数的图像 已知a＞0且a≠1，函数y=ax与y=loga(-x)的图像只能是（ ）【分析】应先由函数定义域判断图像的位置，再对底数a进行讨论，最后选出正确选项.【解析】解法一:首先,曲线y=ax只可能在上半平面,y=loga(-x)只可能在左半平面上,从而排除A,C.
其次,从单调性着眼,y=ax与y=loga(-x)的增减性正好相反,又可排除D.
故应选B.【评析】要正确识别函数的图像，一是要熟悉各种基本初等函数的图像，如一次函数、二次函数、反比例函数、指数函数、对数函数的图像等；二是把握函数图像的性质，根据图像的性质去判断，如过定点、定义域、值域、单调性、奇偶性等.解法二:若0若a>1,则曲线y=ax上升且过(0,1),而曲线y=loga(-x)下降且过(-1,0),只有B满足条件.
解法三:如果注意到y=loga(-x)的图象关于y轴的对称图象为y=logax,又y=logax与y=ax互为反函数(图象关于直线y=x对称),则可直接选定B.函数y=ax与y=-logax(a＞0,a≠1,x＞0)在同一坐标系中的图像形状只能是（ ）(a＞1时,y=ax是增函数,y=logax
也是增函数，∴y=-logax为减函数.
∴两函数的单调性相反，除C，D,
而B中，y=-logax中x＜0不成立.
故应选A.)A学点五 求最值已知f(x)=2+log3x,x∈［1,9］,求y=［f(x)］2+f(x2)的最大值及当y取最大值时x的值.【分析】要求函数y=［f(x)］2+f(x2)的最大值，首先要求函数的解析式，然后求出函数的定义域，最后用换元法求出函数的值域.【解析】∵f(x)=2+log3x,
∴y=［f(x)］2+f(x2)=(2+log3x)2+(2+log3x2)
=log32x+6log3x+6
=(log3x+3)2-3.
∵函数f(x)的定义域为［1,9］,
∴要使函数y=［f(x)］2+f(x2)有定义，必须 1≤x2≤9
1≤x≤9.
∴1≤x≤3,∴0≤log3x≤1.
令u=log3x，则0≤u≤1.
又∵函数y=(u+3)2-3在［-3,+∞)上是增函数,
∴当u=1时，函数y=(u+3)2-3有最大值13.
即当log3x=1,即x=3时，函数y=［f(x)］2+f(x2)有最大值为13.【评析】求函数的值域和最值，必须考虑函数的定义域，同时应注意求值域或最值的常用方法.已知x满足不等式-3≤ ≤ ,求函数f(x)=
的最大值和最小值.∵-3≤ ≤ ，即 ≤x≤8,
∴ ≤log2x≤3,
∵f(x)=(log2x-2)·(log2x-1)=（log2x- ）2 - ,
∴当log2x= ,即x=2 时，f(x)有最小值- .
又∵当log2x=3,即x=8时，f(x)有最大值2,
∴f(x)min=- ,f(x)max=2.学点六 求变量范围已知函数f(x)=lg(ax2+2x+1).
（1）若f(x)的定义域为R，求实数a的取值范围；
（2）若f(x)的值域为R，求实数a的取值范围.【分析】若f(x)的定义域为R，则对一切x∈R,f(x)有意义；若f(x)值域为R，则f(x)能取到一切实数值.【解析】（1）要使f(x)的定义域为R，只要使μ(x)=ax2+2x+1的值恒为正值，
∴ a>0
Δ=4-4a<0，（2）若f(x)的值域为R，则要求μ(x)=ax2+2x+1的值域包含(0,+∞).
当a<0时，这不可能；当a=0时，μ(x)=2x+1∈R成立；当a>0时，μ(x)=ax2+2x+1要包含(0,+∞)，需
a>0
Δ=4-4a≥0?
综上所述，0 ≤a≤1.【评析】本题两小题的函数的定义域与值域正好错位.
（1）中函数的定义域为R,由判别式小于零确定；
（2）中函数的值域为R，由判别式不小于零确定.函数y=logax在x∈［2,+∞)上总有|y|>1，求a的取值范围.依题意得|logax|>1对一切x∈［2,+∞)都成立，
当a>1时，因为x≥2,所以|y|=logax>1，即logax>log22.所以1当01,所以logax<-1，即logax综上，可知a的取值范围为a∈（ ,1）∪(1,2).学点七 对数的综合应用已知函数f(x)= .
（1）判断f(x)的奇偶性；
（2）证明：f(x)在(1,+∞)上是增函数.【分析】由函数的奇偶性、单调性的证明方法作出证明.【评析】无论什么函数，证明单调性、奇偶性，定义是最基本、最常用的方法.
u(x1)-u(x2)=
∵x2>x1>1,
∴x2-x1>0,x1-1>0,x2-1>0,
∴u(x1)-u(x2)>0,即u(x1)>u(x2)>0,
∵y=log u在(0,+∞)上是减函数,
∴log u(x1)即log ∴f(x1)∴f(x)在(1,+∞)上是增函数.设f(x)=log2 +log2(x-1)+log2(p-x).
（1）求函数f(x)的定义域；
（2）f(x)是否存在最大值或最小值？如果存在，请把它求出来;如果不存在，请说明理由.
（1）由 >0
x - 1>0
p - x>0?
∴当p>1时，函数f(x)的定义域为(1,p)(p>1).（2）因为f(x)=
所以当 ≤1,即1值；当1< 3,x= 时，f(x)取得最大
值，log2 =2log2(p+1)-2，但无最小值学点八 反函数已知a>0,且a≠1，函数y=ax与y=loga(-x)的图象只能是（ ）【分析】分a>1,0其次，从单调性着手，y=ax与y=loga(-x)的增减性正好相反，又可排除D，故只能选B.
解法二：若01，则曲线y=ax上升且过点(0,1)，而曲线y=loga(-x)下降且过(-1,0)，只有B满足条件.
解法三：如果注意到y=loga(-x)的图象关于y轴的对称图象为y=logax的图象，因为y=logax与y=ax互为反函数（图象关于直线y=x对称），则可直接选B.【评析】本题可以从图象所在的位置及单调性来判别，也可利用函数的性质识别图象，特别注意底数a对图象的影响.要养成从多角度分析问题、解决问题的习惯，培养思维的灵活性.原函数y=f(x)与其反函数的图象关于y=x对称是其重要性质.若函数f(x)=ax(a>0，且a≠1)的反函数的图象过点
(2,-1),则a= . 反函数的图象过点(2,-1)，则f(x)=ax的图象过
(-1,2),得a-1=2,a= .1.如何确定对数函数的单调区间？（1）图象法：此类方法的关键是图象变换.
（2）形如y=logaf(x)的函数的单调区间的确定方法：
首先求满足f(x)>0的x的范围，即求函数的定义域.假设f(x)在定义域的子区间I1上单调递增，在子区间I2上单调递减，则
①当a>1时，原函数与内层函数f(x)的单调区间相同，即在I1上单调递增，在I2上单调递减.
②当0对数函数与指数函数的学习要对比着进行，如它们的定义域和值域互换，它们的单调性与底数a的关系完全一致，指数函数和对数函数的图象分别过点(0,1)和点(1,0)等，这样有助于理解和把握这两个函数.3.如何理解反函数？学习过程中要注意指数函数与对数函数的关系和它们间的相互转化，掌握反函数的图象关于直线y=x对称，在解决有关指数函数和对数函数的问题时，要注意数形结合，注意运用复合函数“同增异减”的单调性原则，注意分类讨论.1.在指数函数与对数函数中，对底数的要求是一致的，均是a>0，且a≠1.但指数函数的定义域是R，对数函数的定义域是(0,+∞).对数函数的图象在y轴的右侧，真数大于零，这一切必须熟记.
2.反函数
（1）在写指数函数或对数函数的反函数时，注意函数的定义域且底数必须相同；
（2）互为反函数的两个函数在各自的定义域内单调性相同；（3）对数函数与指数函数互为反函数，因此，对数函数图象画法有两种：一是描点法，二是利用指数函数与对数函数互为函数的关系作图；
（4）互为反函数的两个函数的定义域与值域发生互换，即原函数的定义域是反函数的值域，原函数的值域是反函数的定义域；
（5）互为反函数的两函数的图象关于直线y=x对称.祝同学们学习上天天有进步！