函数的表示法一

课件21张PPT。学点一学点二学点三学点四学点五
1.通过列出自变量与对应函数值的表格来表达函数关系的方法叫 .
2.用图象来表示两个变量之间的函数关系的方法叫 .
3.在函数y=f(x)(x∈A)中，f(x)是用代数式来表达的，这种表示函数的方法叫 .
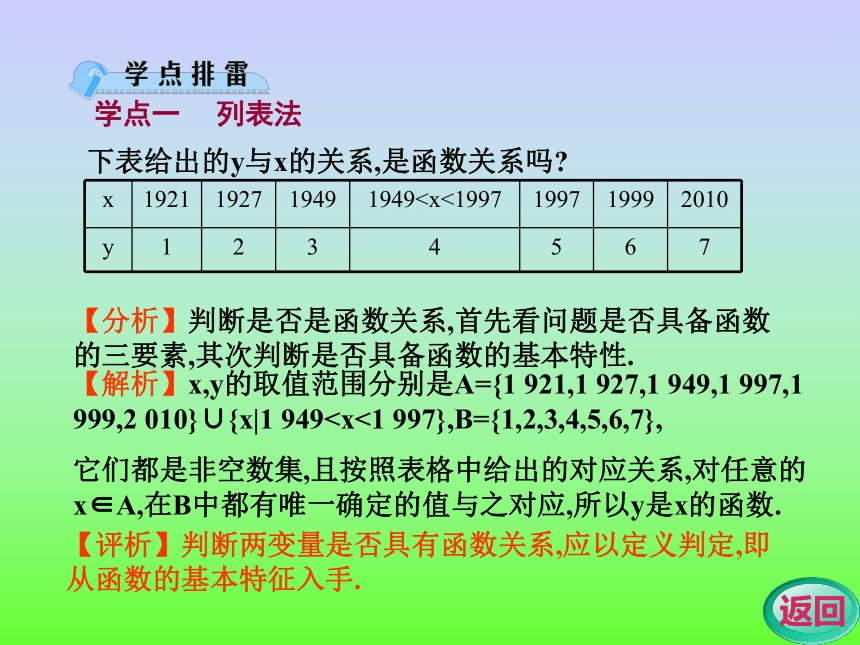
列表法图象法解析法学点一 列表法下表给出的y与x的关系,是函数关系吗?【分析】判断是否是函数关系,首先看问题是否具备函数的三要素,其次判断是否具备函数的基本特性.【解析】x,y的取值范围分别是A={1 921,1 927,1 949,1 997,1 999,2 010}∪{x|1 949它们都是非空数集,且按照表格中给出的对应关系,对任意的x∈A,在B中都有唯一确定的值与之对应,所以y是x的函数.【评析】判断两变量是否具有函数关系,应以定义判定,即从函数的基本特征入手.下表所示为x与y间的关系：那么它的解
析式是( )
A.y=100-10x B.y=100-5x2 C.y=100-5x-5x2 D.y=20-x-x2C【评析】函数的图象是函数的直观描述，结合学过的基本初等函数，可作出一般的函数图象.
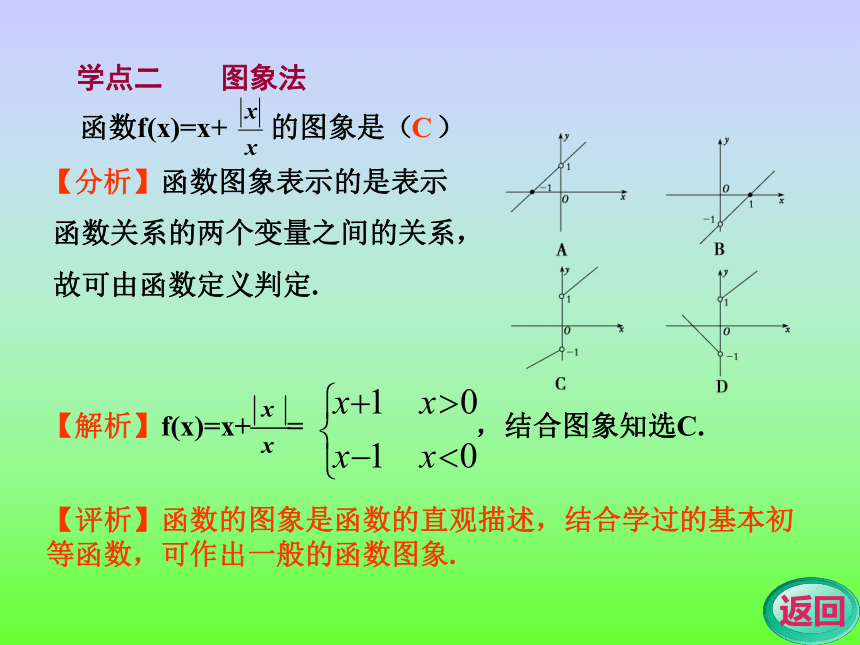
学点二 图象法 【分析】函数图象表示的是表示
函数关系的两个变量之间的关系，
故可由函数定义判定.函数f(x)=x+ 的图象是（ ）【解析】f(x)=x+ = ，结合图象知选C.C作出下列函数的图象.
(1)y=1-x(x∈Z);
(2)y=2x2-4x-3(0≤x<3).(1)这个函数的图象由一些点组成,这些点都在直线y=1-x上(∵x∈Z,从而y∈Z),这些点称为整点(如图甲).
(2)∵0≤x<3,∴这个函数的图象是抛物线y=2x2-4x-3介于0≤x<3之间的一段曲线(如图乙).学点三 求函数解析式（1）如果 ，则f(x)= ;
（2）如果 ,则f(x+1)= ;
（3）如果f［f(x)］=2x-1，则一次函数f(x)= ;
（4）如果函数f(x)满足方程af(x)+ =ax,x∈R,且x≠0,a为常数，且a≠±1,则f(x)= .【分析】求f(x)的关键就在于弄清相对于“x”而言，
“f”是一种怎样的对应关系.【解析】（1）∵ ∴ .
（2）∵
∴f(x)=x2+4, ∴f(x+1)=(x+1)2+4.
（3）∵f(x)为一次函数，设f(x)=kx+b(k≠0),
∴f［f(x)］=f(kx+b)=k(kx+b)+b=k2x+kb+b=2x-1.
比较系数得
或 .（4）∵ ,用 替换上式中的x得
∴由
可得【评析】①求f(x)解析式的方法比较多，如上述例子中就分别用了换元法、配方法、待定系数法、解方程组的方法，其他方法请试用.
②换元法求f(x)是常用的方法，但要特别注意正确确定中间变量的取值范围，否则就不能正确确定f(x)的定义域.
③（4）题的解法基于这样一种认识：函数是定义域到值域上的映射，定义域中的每一个元素都应满足函数表达式.在已知条件下，x满
足已知的式子，那么 在定义域内也满足这个式子，这样就得到两个关于f(x)与 的方程，因而能解出f(x).（1）已知f( )=x+2 ,求f(x)；
（2）已知 求f(x);
（3）已知函数f(x)满足 ，求f(x)的表达式.（1）解法一：
解法二：令t= +1,则x=(t-1)2(t≥1)，代入原式有
f(t)=(t-1)2+2(t-1)=t2-2t+1+2t-2=t2-1,
∴f(x)=x2-1(x≥1). 学点四 由函数图象求函数解析式已知函数f(x)在［-1,2］上的图象如图所示，求f(x)的解析式.【分析】由图象特点先确定函数类型，再求解析式.【评析】熟练掌握学过的函数图象，有利于这类问题的解决.【解析】当-1≤x≤0时，设y=ax+b,
∵过点(-1,0)和(0,1),∴
同样，当0∴函数y=f(x)的图象如图所示，则函数y=f(x)的解析式为（ ）
A.f(x)=(x-a)2(b-x) B.f(x)=(x-a)2(x+b)
C.f(x)=-(x-a)2(x+b) D.f(x)=(x-a)2(x-b)（由图象知,当x=b时,f(x)=0,故排除B,C；又当x>b时,f(x)<0.故排除D.
故应选A.）A学点五 应用问题用长为l的铁丝弯成下部为矩形,上部为半圆形的框架,
若矩形底边长为2x,求此框架围成的面积y与x的函数
关系式,并写出其定义域.【分析】要表示y,需先用x表示出矩形的另一边长.【解析】∵AB=2x,∴弧长CD =πx,AD= .
∴y=
∴函数关系式为 ,其定义域为 .【评析】由实际问题求函数解析式,先进行分析,找出
所需的中间量,如本题中的AD.同时要十分重视函数的定义域.某农产品去年各季度的市场价格如下表：
今年某公司计划按去年各季度市场价的“最佳近似值m”（m是与上表中各售价差的平方和取最小值时的值）收购该种农产品，并按每100元纳税10元（又称征税率为10个百分点），计划可收购a万担.政府为了鼓励收购公司多收购这种农产品，决定将税率降低x个百分点，预测收购量可增加2x个百分点.
（1）根据题中条件填空，m= 元/担；
（2）写出税收y（万元）与x的函数关系式.设平方和为y，则
（1）y=(m-195.5)2+(m-200.5)2+(m-204.5)2+(m-199.5)2=
4m2-2×(195.5+200.5+204.5+199.5)m+195.52+200.52+
204.52+199.52取最小值时，
m= =200.
故应填200.
（2）降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担，收购总金额200·a(1+2x%)，依题意得
y=200a(1+2x%)(10-x)%= a·(100+2x)(10-x)
= a·(100+2x)(10-x)(0(1)由具体的实际问题建立函数关系求解析式，一般是通过研究自变量、函数及其他量之间的等量关系，将函数用自变量和其他量的关系表示出来.需要注意的是，一定不能忘记确定自变量的取值范围.
(2)由含有函数f(x)的关系式求f(x)，一般采用配凑法、换元法、待定系数法及解方程组等方法.2.简单函数图象的画法有哪些？
（1）描点法.这是作函数图象的基本方法.用描点法作函数图象的基本操作步骤：首先就函数的关系式探讨函数的一些性质，如定义域、值域以及后面要学到的奇偶性、单调性等，从而对函数图象的轮廓有一个大致的认识；然后选点，将x与y的一些对应值用表列出（对一些不熟悉的函数的值，有条件的可用函数计算器计算得出）；再将表中的x,y的对应值作为点的坐标在坐标系中描出；最后用平滑的曲线依次连结各点即可.
（2）函数图象变换法.为了简化函数图象的作法，我们可以利用后面将要学到的一些知识，利用图象的点对称、轴对称以及图象的移动等变换方法快捷地将函数的图象画出.1.把两个变量之间的函数关系，用一个等式来表示，这个等式就叫做这个函数的解析表达式，简称解析式.用解析法表示函数的优点是函数关系清楚，易从自变量的值求出其对应的函数值，便于用解析式来研究函数的性质.求函数f(x)的解析式常用的方法：
（1）如果已知函数式较简单时，可用直接法求解.
（2）如果已知复合函数f［g(x)］的表达式时，可用换元法求解，但要注意在换元时引起的定义域的变化.最后结果要注明所求函数的定义域.
（3）如果已知函数的种类时，可用待定系数法求解.
2.列表法就是列出表格来表示两个变量的函数关系.其优点为不必通过计算就知道当自变量取某些值时函数的对应值.
3.图象法就是用函数图象表示两个变量之间的关系.其优点为能直观形象地表示出函数的变化情况.祝同学们学习上天天有进步！