幂函数

课件24张PPT。学点一学点二学点三学点四学点五1.一般地,函数y=xa叫做 ，其中x是自变量,a是常数.
2.幂函数y=xa具有下面性质：
（1）所有的幂函数在区间 上都有定义，并且函数图象都通过 点.
（2）如果a>0，则幂函数的图象都通过点 ，并且在区间 上是增函数.
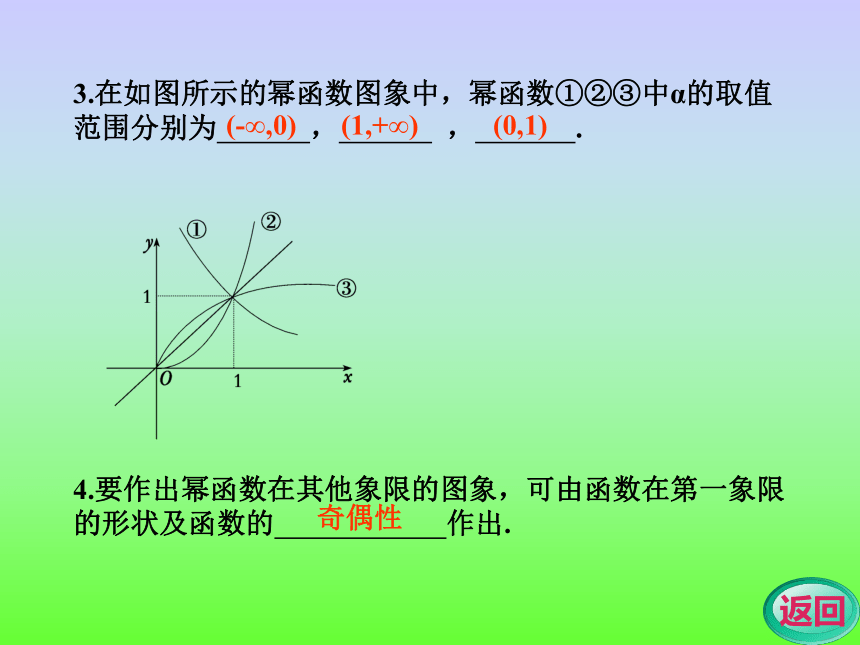
（3）如果a<0，则幂函数在区间 上是减函数，当x从右边趋向于 时，图象在y轴右方无限地逼近 ；当x趋向于+∞时，图象在x轴上方无限地逼近 轴.幂函数(0,+∞)(1,1)(0,0)［0,+∞)(0,+∞)y轴y轴x3.在如图所示的幂函数图象中，幂函数①②③中α的取值范围分别为 ， ， .

4.要作出幂函数在其他象限的图象，可由函数在第一象限的形状及函数的 作出.(-∞,0)(1,+∞)(0,1)奇偶性学点一 幂函数的定义【分析】根据幂函数、正比例函数、反比例函数的定义可求.（2）由题意得 a2-5a+5=1
a2-3a+2≠0,
（3）由题意得 a2-5a+5=-1
a2-3a+2≠0, 【评析】正确理解幂函数与以往所学函数的关系，有利于温故知新.学点二 比较大小【分析】依据幂函数的图象和性质比较大小.【评析】比较大小题要综合考虑函数的性质，特别是单调性的应用，更要善于运用“搭桥法”进行分组，常数0和1是常用的参数.学点三 奇偶性的判定【分析】判定函数奇偶性应用函数奇偶性定义. 判断下列函数的奇偶性 【评析】一般先将函数式化成正指数幂或根式形式，确定定义域，再用定义判断奇偶性；也可通过图象特征来判断.学点四 幂函数的单调性【分析】由函数单调性定义作出证明.【评析】在证明函数的单调性时，既可以用作差的方法，也可以用作商的方法，都可以证明函数f(x)=x在［0,+∞)上是增函数.已知函数f(x)= - xm,且f(4)=- .
（1）求m的值；
（2）判断f(x)在(0,+∞)上的单调性.(1)f(4)= -4m=-72,
即4m=4,∴m=1.
∴f(x)= -x.(2)任取x1,x2∈(0,+∞),且x1f(x1)-f(x2)= -x1-( -x2)
=( - )-(x1-x2)
= -(x1-x2)
=
∵x2-x1>0,x1x2>0,
∴f(x1)-f(x2)>0,
即函数f(x)在(0,+∞)上单调递减.学点五 幂函数的简单应用【分析】根据幂函数图象、单调性比较大小.【解析】（1）∵根据幂函数y=x1.3的图象知当01时,y>1，∴1.30.7>1,于是有0.71.3<1.30.7,
考查幂函数y=xm，由(0.71.3)m<(1.30.7)m知,当x>0时，随着x增大，函数值也增大，∴m>0.（2）∵函数y=x 与y=x 的定义域都是R，y=x 的图
象分布在第一、二象限；y=x 的图象分布在第一、三象限.
∴当x∈(-∞,0)时，x >x ;
当x=0时，显然不合题意；
当x∈(0,+∞)时，x >0,x >0, =x >1, ∴x>1.
即x>1时，x >x .
综上所述，满足条件的x的取值范围为{x|x<0或x>1}.
【评析】由幂函数不等式求变量范围，实质上仍是对图象与单调性的考查.
1.学习幂函数时，应注意什么问题？
（1）并不是任意的一次函数、二次函数都是幂函数，如y=x+1,y=x2-2x都不是幂函数.
（2）求幂函数的定义域时，可分四种情况：一是α为正整数；二是α为正分数；三是α为负整数；四是α为负分数.2.如何更好地掌握幂函数的图象与性质？
要想更好地掌握幂函数的图象与性质，首先必须熟练地掌握幂函数在第一象限的图象与性质，其次掌握幂函数的奇偶性，这样幂函数的图象由对称性即可确定其完整图形，则其性质即可由图象得到.1.把握好幂函数定义的结构特点
幂函数定义仍是结构定义，其特点是xα的系数为1，底数是自变量x的系数为1的单项式.
2.幂函数定义域的求法
幂函数的定义域随着α取值不同而不同,若遇到分数指数型幂函数，应先化为根式，再由根式性质求定义域.3.幂函数图象凸凹性
（1）当α>1时，在第一象限为下凹的；
（2）当0<α<1时，在第一象限为上凸的；
（3）当α<0时，在第一象限为下凹的.
4.幂函数的单调性与奇偶性
（1）单调性要由α的取值范围确定；
（2）奇偶性讨论：由于我们主要研究指数为分数的幂函数，因而先将其化为根式，再由奇偶性定义判断.
祝同学们学习上天天有进步！