方程的根与函数的零点
图片预览








文档简介
课件22张PPT。学点一学点二学点三学点四1.函数零点的概念
对于函数y=f(x),我们把使 的实数x叫做函数y=f(x)的 .
2.函数零点与方程根的关系
函数y=f(x)的零点就是方程f(x)=0的 ,也就是函 数y=f(x)的图象与 的交点的 .所以方程 f(x)=0有 ? 函数y=f(x)的图象与 ? 函数y=f(x) . f(x)=0零点实数根x轴横坐标实数根x轴有交点有零点3.函数零点的判断
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b) ,那么,函数y=f(x)在区间 内有零点,即存在c∈(a,b),使得 ,这个c也就是方程f(x)=0的根.
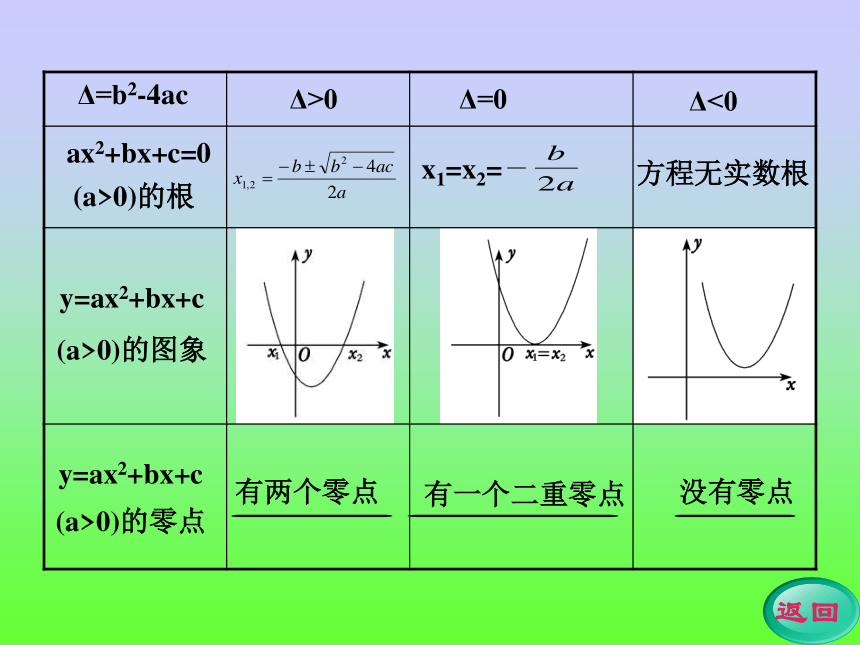
4.二次函数的零点、二次函数图象与x轴的交点、一元二次方程的根三者之间的关系.<0(a,b)f(c)=0有两个零点Δ=b2-4acΔ>0Δ<0Δ=0ax2+bx+c=0(a>0)的根y=ax2+bx+c
(a>0)的图象y=ax2+bx+c(a>0)的零点方程无实数根x1=x2=有一个二重零点没有零点学点一 函数的零点求下列函数的零点:
(1)f(x)=4x-3;
(2)f(x)=-x2-2x+3;
(3)f(x)=x4-1.【分析】根据函数零点与方程的根之间的关系,要求函数的零点就是求相应方程的实数根.【解析】
(1)由f(x)=4x-3=0得x= ,所以函数的零点是 .
(2)由于f(x)=-x2-2x+3=-(x+3)(x-1),因此方程f(x)=0的根为-3,1,故函数的零点是-3,1.
(3)由于f(x)=x4-1=(x2+1)(x+1)(x-1),令f(x)=0,得x=1,-1,故函数的零点是1,-1.【评析】求函数的零点就是求相应方程的实数根,一般可以借助求根公式或因式分解等方法求出方程的根,从而得到函数的零点.(1)令lnx-3=0,得x=e3,
∴函数的零点为x=e3.
(2)方程x3-7x+6=0可化为
x3-6x-x+6=x(x2-1)-6(x-1)=x(x+1)(x-1)-6(x-1)
=(x-1)(x2+x-6)=(x-1)(x-2)(x+3)=0.
即(x-1)(x-2)(x+3)=0得x1=-3,x2=1,x3=2,
∴函数y=-x2-2x+3的零点为1,-3;
函数y=x3-7x+6的零点为-3,1,2.求下列函数的零点:
(1)y=lnx-3; (2)y=x3-7x+6.学点二 判断零点判断函数f(x)=x2-x-6的零点是否存在,若存在,说明零点所在的一个区间.【分析】要判断函数的零点的个数,实际就是考查方程x2-x-6=0的解的个数,即y=x2-x-6的图象与x轴的交点个数.【解析】考查函数f(x)=x2-x-6
知图象为抛物线(如图所示),
容易看出f(0)=-6<0,f(4)=6>0,f(-4)=14>0.【评析】
(1)方程的解与函数零点的关系是解决本题的桥梁;
(2)体会数形结合和函数与方程的思想的运用.由于函数f(x)的图象是连续曲线,因此,点B(0,-6)与点C(4,6)之间的那部分曲线必然穿过x轴,即在区间(0,4)内必有一个点x1,使f(x1)=0;同样在区间(-4,0)内也必有一个点x2,使f(x2)=0,所以函数f(x)=x2-x-6有两个零点,分别在区间(0,4)和(-4,0)内.求证:方程5x2-7x-1=0的根一个在区间(-1,0)上,另一个在区间(1,2)上.证明:令f(x)=5x2-7x-1,则
f(0)=-1,f(1)=-3,f(-1)=11,f(2)=5.
由f(-1)>0,f(0)<0知在(-1,0)上f(x)有一个零点,即方程f(x)=0有一根,
同理,由f(1)<0,f(2)>0知方程在(1,2)上也有一根.学点三 函数值符号的判定函数y=-2x2+x+3的自变量x分别在什么范围内取值时,函数值大于0,小于0,等于0?【分析】首先求出函数的零点,然后利用零点,结合函数的两个性质,可以求出函数值大于0,小于0,等于0时自变量x的取值范围.【解析】由-2x2+x+3=0得x1=-1,x2= ,所以函数的零
点是-1和 ,亦即当自变量x取-1和 时,函数值等于0.
函数的两个零点-1和 将数轴分成3个区间:(-∞,-1),(-1, ),( ,+∞),在区间(-1, )内取特殊值x=0,得其函数值f(0)=3>0,依函数零点的性质
(2)知当x∈(-1, )时,有f(x)>0;再依据函数零
点的性质(1)知,当x∈(-∞,-1)和x∈( ,+∞)时,
都有f(x)<0.
因此,当自变量x∈(-1, )时,函数值大于0;
当x∈(-∞,-1)∪( ,+∞)时,函数值小于0;
当x=-1和 时,函数值等于0.【评析】求出函数的零点后,充分利用函数零点的两个性质,得到在不同的自变量的取值范围内,函数值的不同取值情况.求函数y=x2-2x-8在y>0时,x的取值范围.
解:∵y=x2-2x-8=(x+2)(x-4),
∴函数的两个零点是-2和4,由图象可知
当x∈(-∞,-2)∪(4,+∞)时,y>0.学点四 零点与不等式已知函数f(x)=x3-4x.
(1)求函数的零点并画函数的图象;
(2)解不等式:xf(x)<0.【分析】由函数的零点判断作出函数图象.【解析】
(1)因为 x3-4x= x(x-2)(x+2),所以函数的零点为0,-2,2.三个零点把数轴分成4个区间:(-∞,-2],(-2,0],(0,2],(2,+∞).由于相邻两个零点之间的所有函数值保持同号,函数的图象如图所示.(2)不等式xf(x)<0?
x>0 x<0
f(x)<0 f(x)>0,
结合函数图象,得不等式的解集为(0,2)∪(-2,0).【评析】根据函数的零点定义与性质,可以用来帮助画函数的图象,结合函数图象不仅可以直观的研究函数的性质,而且能够求解相关的不等式,这体现了以数辅形,以形助数的思想方法.已知函数f(x)=x2+2x-3m,当x∈(0,+∞)时,f(x)>0,求m的取值范围.可分两种情况处理,即分无零点和有零点。
(1)当f(x)无零点时,Δ=4+12m<0,解得m<- .
所以当m<- 时,对于x∈(0,+∞),有f(x)>0.
(2)当f(x)有零点,且又满足x∈(0,+∞)时,f(x)>0,
有两个零点必落在(-∞,0)内,此时有
Δ≥0 m≥-
-ba≤0 -2≤0
ca≥0, -3m≥0,即 解得- ≤m≤0.
综上所述,得当x∈(0,+∞),f(x)>0时,m的取值范围是
m≤0.1.怎样判定函数f(x)在[a,b]上是否有零点?判定f(x)在区间[a,b]上是否有零点,可用下面方法:
(1)函数在区间[a,b]上的图象连续,且它在区间[a,b]端点的函数值异号,则函数在[a,b]上一定存在零点;
(2)函数图象连续且在区间[a,b]上存在零点,则它在区间[a,b]端点的函数值可能异号,也可能同号;
上述方法只能用来判断函数零点的存在性,不能用来判断函数零点的个数.2.怎样理解函数零点与方程根的关系?
3.函数值与零点有什么关系?返回目录设给出函数y=f(x),则有方程f(x)=0有实数根?函数y=f(x)有零点?函数y=f(x)的图象与x轴有交点.
若方程f(x)=0有二重实根,则称函数y=f(x)有二阶零点.对于任意函数y=f(x),只要它的图象是连续不间断的,则有
(1)当通过零点时,函数值变号.如函数y=x2-x-6的图象在零点-2的左边时,函数值取正号;向右通过零点-2时,函数值由正变负;继续向右通过零点3时,函数值又由负变正.
(2)在相邻两个零点之间所有的函数值保持同号.2.求出函数的零点后,充分利用函数零点的两个性质,得到在不同的自变量的取值范围内,函数值的不同取值情况.1.求函数的零点就是求相应方程的实数根,一般可以借助求根公式或因式分解等方法求出方程的根,从而得到函数的零点.祝同学们学习上天天有进步!
对于函数y=f(x),我们把使 的实数x叫做函数y=f(x)的 .
2.函数零点与方程根的关系
函数y=f(x)的零点就是方程f(x)=0的 ,也就是函 数y=f(x)的图象与 的交点的 .所以方程 f(x)=0有 ? 函数y=f(x)的图象与 ? 函数y=f(x) . f(x)=0零点实数根x轴横坐标实数根x轴有交点有零点3.函数零点的判断
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b) ,那么,函数y=f(x)在区间 内有零点,即存在c∈(a,b),使得 ,这个c也就是方程f(x)=0的根.
4.二次函数的零点、二次函数图象与x轴的交点、一元二次方程的根三者之间的关系.<0(a,b)f(c)=0有两个零点Δ=b2-4acΔ>0Δ<0Δ=0ax2+bx+c=0(a>0)的根y=ax2+bx+c
(a>0)的图象y=ax2+bx+c(a>0)的零点方程无实数根x1=x2=有一个二重零点没有零点学点一 函数的零点求下列函数的零点:
(1)f(x)=4x-3;
(2)f(x)=-x2-2x+3;
(3)f(x)=x4-1.【分析】根据函数零点与方程的根之间的关系,要求函数的零点就是求相应方程的实数根.【解析】
(1)由f(x)=4x-3=0得x= ,所以函数的零点是 .
(2)由于f(x)=-x2-2x+3=-(x+3)(x-1),因此方程f(x)=0的根为-3,1,故函数的零点是-3,1.
(3)由于f(x)=x4-1=(x2+1)(x+1)(x-1),令f(x)=0,得x=1,-1,故函数的零点是1,-1.【评析】求函数的零点就是求相应方程的实数根,一般可以借助求根公式或因式分解等方法求出方程的根,从而得到函数的零点.(1)令lnx-3=0,得x=e3,
∴函数的零点为x=e3.
(2)方程x3-7x+6=0可化为
x3-6x-x+6=x(x2-1)-6(x-1)=x(x+1)(x-1)-6(x-1)
=(x-1)(x2+x-6)=(x-1)(x-2)(x+3)=0.
即(x-1)(x-2)(x+3)=0得x1=-3,x2=1,x3=2,
∴函数y=-x2-2x+3的零点为1,-3;
函数y=x3-7x+6的零点为-3,1,2.求下列函数的零点:
(1)y=lnx-3; (2)y=x3-7x+6.学点二 判断零点判断函数f(x)=x2-x-6的零点是否存在,若存在,说明零点所在的一个区间.【分析】要判断函数的零点的个数,实际就是考查方程x2-x-6=0的解的个数,即y=x2-x-6的图象与x轴的交点个数.【解析】考查函数f(x)=x2-x-6
知图象为抛物线(如图所示),
容易看出f(0)=-6<0,f(4)=6>0,f(-4)=14>0.【评析】
(1)方程的解与函数零点的关系是解决本题的桥梁;
(2)体会数形结合和函数与方程的思想的运用.由于函数f(x)的图象是连续曲线,因此,点B(0,-6)与点C(4,6)之间的那部分曲线必然穿过x轴,即在区间(0,4)内必有一个点x1,使f(x1)=0;同样在区间(-4,0)内也必有一个点x2,使f(x2)=0,所以函数f(x)=x2-x-6有两个零点,分别在区间(0,4)和(-4,0)内.求证:方程5x2-7x-1=0的根一个在区间(-1,0)上,另一个在区间(1,2)上.证明:令f(x)=5x2-7x-1,则
f(0)=-1,f(1)=-3,f(-1)=11,f(2)=5.
由f(-1)>0,f(0)<0知在(-1,0)上f(x)有一个零点,即方程f(x)=0有一根,
同理,由f(1)<0,f(2)>0知方程在(1,2)上也有一根.学点三 函数值符号的判定函数y=-2x2+x+3的自变量x分别在什么范围内取值时,函数值大于0,小于0,等于0?【分析】首先求出函数的零点,然后利用零点,结合函数的两个性质,可以求出函数值大于0,小于0,等于0时自变量x的取值范围.【解析】由-2x2+x+3=0得x1=-1,x2= ,所以函数的零
点是-1和 ,亦即当自变量x取-1和 时,函数值等于0.
函数的两个零点-1和 将数轴分成3个区间:(-∞,-1),(-1, ),( ,+∞),在区间(-1, )内取特殊值x=0,得其函数值f(0)=3>0,依函数零点的性质
(2)知当x∈(-1, )时,有f(x)>0;再依据函数零
点的性质(1)知,当x∈(-∞,-1)和x∈( ,+∞)时,
都有f(x)<0.
因此,当自变量x∈(-1, )时,函数值大于0;
当x∈(-∞,-1)∪( ,+∞)时,函数值小于0;
当x=-1和 时,函数值等于0.【评析】求出函数的零点后,充分利用函数零点的两个性质,得到在不同的自变量的取值范围内,函数值的不同取值情况.求函数y=x2-2x-8在y>0时,x的取值范围.
解:∵y=x2-2x-8=(x+2)(x-4),
∴函数的两个零点是-2和4,由图象可知
当x∈(-∞,-2)∪(4,+∞)时,y>0.学点四 零点与不等式已知函数f(x)=x3-4x.
(1)求函数的零点并画函数的图象;
(2)解不等式:xf(x)<0.【分析】由函数的零点判断作出函数图象.【解析】
(1)因为 x3-4x= x(x-2)(x+2),所以函数的零点为0,-2,2.三个零点把数轴分成4个区间:(-∞,-2],(-2,0],(0,2],(2,+∞).由于相邻两个零点之间的所有函数值保持同号,函数的图象如图所示.(2)不等式xf(x)<0?
x>0 x<0
f(x)<0 f(x)>0,
结合函数图象,得不等式的解集为(0,2)∪(-2,0).【评析】根据函数的零点定义与性质,可以用来帮助画函数的图象,结合函数图象不仅可以直观的研究函数的性质,而且能够求解相关的不等式,这体现了以数辅形,以形助数的思想方法.已知函数f(x)=x2+2x-3m,当x∈(0,+∞)时,f(x)>0,求m的取值范围.可分两种情况处理,即分无零点和有零点。
(1)当f(x)无零点时,Δ=4+12m<0,解得m<- .
所以当m<- 时,对于x∈(0,+∞),有f(x)>0.
(2)当f(x)有零点,且又满足x∈(0,+∞)时,f(x)>0,
有两个零点必落在(-∞,0)内,此时有
Δ≥0 m≥-
-ba≤0 -2≤0
ca≥0, -3m≥0,即 解得- ≤m≤0.
综上所述,得当x∈(0,+∞),f(x)>0时,m的取值范围是
m≤0.1.怎样判定函数f(x)在[a,b]上是否有零点?判定f(x)在区间[a,b]上是否有零点,可用下面方法:
(1)函数在区间[a,b]上的图象连续,且它在区间[a,b]端点的函数值异号,则函数在[a,b]上一定存在零点;
(2)函数图象连续且在区间[a,b]上存在零点,则它在区间[a,b]端点的函数值可能异号,也可能同号;
上述方法只能用来判断函数零点的存在性,不能用来判断函数零点的个数.2.怎样理解函数零点与方程根的关系?
3.函数值与零点有什么关系?返回目录设给出函数y=f(x),则有方程f(x)=0有实数根?函数y=f(x)有零点?函数y=f(x)的图象与x轴有交点.
若方程f(x)=0有二重实根,则称函数y=f(x)有二阶零点.对于任意函数y=f(x),只要它的图象是连续不间断的,则有
(1)当通过零点时,函数值变号.如函数y=x2-x-6的图象在零点-2的左边时,函数值取正号;向右通过零点-2时,函数值由正变负;继续向右通过零点3时,函数值又由负变正.
(2)在相邻两个零点之间所有的函数值保持同号.2.求出函数的零点后,充分利用函数零点的两个性质,得到在不同的自变量的取值范围内,函数值的不同取值情况.1.求函数的零点就是求相应方程的实数根,一般可以借助求根公式或因式分解等方法求出方程的根,从而得到函数的零点.祝同学们学习上天天有进步!
