集合的基本运算
图片预览







文档简介
课件27张PPT。学点一学点二学点三学点四学点五学点六学点七1.一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的 ,记作 ,即A∪B= 。
2.一般地,由属于集合A且属于集合B的所有元素组成的集合,称为集合A与B的 ,记作 ,即A∩B= .
3.(1)一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为 ,通常记作 .
(2)对于一个集合,由全集U中不属于集合A的所有元素组成的集合称
为集合A相对于全集U的 ,记作 ,
即 .
并集A∪B{x|x∈A或x∈B}交集A∩B{x|x∈A,且x∈B}全集U补 集U?4.(1)1.并集A∪B{x|x∈A或x∈B}对于任意的集合A, B,有A∪A= ,A∩A= ,A∪B= ,
A∩B= .
若A∪B=B,则A B;若A∩B=B,则B A.
(2)由补集的定义可知,对任意集合A,有A∪(CUA)= , A∩(CUA)= .5.用集合语言描述下面几个图:
(1)A B,A∩B= ,A∪B= ;
(2)A B,A∩B= ,A∪B= ;
(3)A =B,A∩B= ,A∪B= .BAABA(B)A(B)AAB∪AB∩AU学点一 基本概念的考查已知U={1,2,3,…,8},A={1,2,3,4},B={2,3,4,5}.求:
(1)A∩B; (2)A∪(CUB);
(3)(CUA)∩(CUB); (4)(CUA)∪(CUB)
【分析】由集合的交、并、补概念直接求解. 【解析】 ∵U={1,2,3,…,8},A={1,2,3,4},B={2,3,4,5},
∴CUA={5,6,7,8}, CUB={1,6,7,8}.
∴(1)A∩B={1,2,3,4}∩{2,3,4,5}={2,3,4}.
(2)A∪(CUB)={1,2,3,4}∪{1,6,7,8}={1,2,3,4,6,7,8}.
(3)(CUA)∩(CUB)={5,6,7,8}∩{1,6,7,8}= {6,7,8}.
(4)(CUA)∪(CUB)={5,6,7,8}∪{1,6,7,8}={1,5,6,7,8 }.【评析】集合的简单运算可由基本概念直接求解.已知集合S={x|1(1)(CSA)∩(CSB); (2)CS(A∪B);
(3)(CSA)∪(CSB); (4)CS(A∩B).解:A∩B={x|3≤x<5}, A∪B={x|2≤x<7},
CSA={x|1(1)(CSA)∩(CSB)={x|1(2)CS(A∪B)={x|1(3)(CSA)∪(CSB)={x|1(4)CS(A∩B)={x|1 P={x|y2=-2(x-3)}={x|x≤3},
∴M∩P={x|x≥-1,且x≤3}={x|-1≤x≤3}.故应选C.学点二 交 集【分析】由集合的定义,集合M表示方程y2=x+1中x的范围,
集合P表示方程y2=-2(x-3)中x的范围,故应先化简集合M,P.【评析】理解集合的表示形式,掌握其意义,利用交 集定义可解决所给问题.
已知集合M={x|y2=x+1},P={x|y2=-2(x-3)},那么M∩P=( )
A. {(x,y)x= ,y=± } B.{x|-1C.{x|-1≤x≤3} D.{x|x≤3 }
C设集合A={(x,y)|2x+y=1,x,y∈R},B={(x,y)|a2x+2y=a,x,y∈R},
若A∩B=?,求a的值.解:集合A,B的元素分别是二元一次方程2x+y=1和a2x+2y=a的解,因为两方程的公共解集A∩B=?,所以方程组无解.
列方程组 得(4-a2)x=2-a
则 即a=-2.
学点三 并 集设A={4,5,6,8},B={3,5,7,8},下列集合中与A∪B相等的集合是( )
A.{4,5,6,7,8} B.{3,4,6,7,10,16}
C.{3,4,5,6,7,8,9} D.{3,4,5,6,7,8}【分析】注意到集合A与集合B的并集的定义中:
(1)集合A∪B中的元素必须是集合A或集合B的元素,
(2)集合A∪B包含集合A与集合B中的所有元素.D【评析】在判定或书写集合A与集合B的并集时,既不能遗
漏元素, 也不能增添元素,要严格地理解、掌握并集的定义.
【解析】A.3∈B,但3?{4,5,6,7,8},{4,5,6,7,8}?A∪B;
B.10?A,10?B,16?A,16?B,{3,4,6,7,10,16}≠A∪B;
C.9?A,9?B,A∪B?{3,4,5,6,7,8,9};
D.显然A∪B={3,4,5,6,7,8}.
故应选D.已知A={x|x≤-1或x≥3},B={x|aA.3≤a<4 B.-1解:∵A={x|x≤-1或x≥3},B={x|a∴由数轴知,a≤-1.
故应选C.C学点四 补集与全集设A={0,2,4,6},CUA={-1,-3,1,3},CUB={-1,0,2},求B.【分析】由A∪(CUA)=U确定全集U,则B可求.【解析】∵A={0,2,4,6},CUA={-1,-3,1,3},
∴U={-3,-1,0,1,2,3,4,6},
又∵CUB={-1,0,2},∴B={-3,1,3,4,6}.【评析】解决与补集有关的问题时,应明确全集是什么,
同时注意补集的有关性质:CU?=U,CUU=?,CU(CUA)=A等.设全集U={2,3,a2+2a-3},A={|2a-1|,2},且CUA={5},求实数a的值.解:∵CUA={5},∴5∈U,且5?A.
∴a2+2a-3=5,即a=2或a= -4.
当a=2时,|2a-1|=3,这时A={3,2},U={2,3,5}.
∴CUA={5},适合题意.∴a=2.
当a=-4时,|2a-1|=9,这时A={9,2},U={2,3,5},A?U,
∴CUA无意义,故a=-4应舍去.
综上所述可知a=2.学点五 交集的应用已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},
若A∪B=A,求实数m的取值范围.【分析】由A∪B=A得A?B,故应从B?A入手讨论,
但考虑到B是A的子集,因此,不要忘记B=?的情况.【解析】由题意,A∪B=A,∴B?A.
(1)若B=?,则m+1>2m-1,即m<2,
此时总有A∪B=A∪?=A成立.
(2)若B≠?,则
解得2≤m≤3.
综合(1)(2)知,m的取值范围是{m|m<2}∪{m|2≤m≤3}={m|m≤3}.
【评析】由A∪B=A可得B?A,而B?A包括两种情况,
即B=?和B≠?.本题常犯的错误是把
B=?漏掉而只讨论B≠?这一种情况.设集合A={a2, a+1,-3},B={a-3,2a-1,a2+1},A∩B={-3},求实数a的值.解:∵A∩B={-3},∴-3∈B.
∴a-3= -3或2a-1= -3,
∴a=0或a= -1.
当a=0时,A={0,1,-3},B={-3,-1,1},此时A∩B={1,-3},与A∩B={-3}矛盾,故舍去.
当a= -1时,A={1,0,-3},B={-4,-3,2},满足A∩B={-3},
∴a= -1.学点六 Venn图的应用【分析】关于集合的交、并、补的问题,通常可以由分析法
找出集合中一定有或一定没有的元素,对它们逐一检验;
或利用Venn图,把元素一一放入图中相应位置,从而写出所
求集合.【解析】解法一:利用Venn图,在图中
标出各个元素的相应位置,可以直接写
出A与B,A={2,3,5,7},B={1,2,9}.若集合U={x|x是小于10的正整数},A?U,B?U,且(CUA)∩B={1,9},
A∩B={2},(CUA)∩(CUB)={4,6,8},试求A与B.解法二:∵A∩B={2},(CUA)∩B={1,9},
∴B=(A∩B)∪[(CUA)∩B]={1,2,9}.
∵A∪B=CU[(CUA)∩(CUB)]={1,2,3,5,7,9},
又∵B={1,2,9},A∩B={2},∴A={2,3,5,7}.【评析】事实上,在解决这类问题时,将Venn图的使用与分
析法相结合更准确简捷.设A,B都是不超过8的正整数组成的全集U的子集A∩B={3},
(CUA)∩(CUB)={1,8},(CUA)∩B={4,6},求集合A,B.解:U={1,2,3,4,5,6,7,8},在Venn图中将1,2,3,4,5,6,7,8分别填入到相应的位置中去,则由A∩B={3},CUA∩CUB={1,8},
(CUA)∩B={4,6}得A∩(CUB)={2,5,7}.
∴A={2,3,5,7},B={3,4,6}.学点七 集合运算的应用已知集合S={1,3,x3+3x2+2x},A={1,|2x-1|},如果CSA={0},
则这样的实数x是否存在?若存在,求出x;若不存在,说明理由.【分析】解决此问题的关键是正确理解CSA={0}的意义,
它有两层含义,即0∈S,但0?A,这样解题思路就清楚了.【评析】解答此题时,我们由CSA={0}求出x1=0,x2=-1,x3=-2之后,验证其是否符合题目的隐含条件A?S是必要的,否则就会误认为x1=0或x3=-2也是所求的实数x,从而得出错误的结论.集合概念及其基本理论是近、现代数学的最基础的内容之一,学好这部分知识的目的之一就是在于应用. 因此,一定要学会读懂集合的语言和符号,并能运用集合的观点研究、判断和处理简单的实际问题.解:(1)如A={1,2,3},B={2,3,4},则A-B={1}.
(2)不一定相等,由(1)知B-A={4},而A-B={1},B-A≠A-B.再如A={1,2,3},B={1,2,3},A-B=?,B-A=? ,此时A-B=B-A.故A-B与B-A
不一定相等.
(3)因为A-B={x|x≥6}, B-A={x|-6由此猜测:一般的对于两个集合A,B,有A-(A-B)=B-(B- A)
设A,B是两个非空集合,定义A与B的差集为A-B={x|x∈A且x?B}.
(1)试举出两个数集A,B,求它们的差集;
(2)差集A-B与B-A是否一定相等?并说明你的理由;
(3)已知A={x|x>4},B={x||x|<6},求A-(A-B)及B-(B-A),由此
你可以得到什么更一般的结论?(不必证明)1.在解题时如何用好集合语言?
解集合问题,不仅仅是运用集合语言,更重要的是明确集合语言所蕴含的真实的数学含义,集合语言的转换过程,实质就是在进行数学问题的等价转换时,向着我们熟悉的能够解决的问题转化.
2.在学习时应注意什么问题?
(1)对于交集、并集、全集、补集等概念的理解,要注意教材中的实例和Venn图的直观作用.
(2)要善于将三者进行比较记忆,找出它们之间的联系与区别.(3)注意在集合运算中,运用Venn图,借助于数轴等几何方法直观理解.
(4)学会集合语言的运用,并逐渐学会用集合的观点研究事物的内涵与外延.
3.怎样理解全集和补集?
全集并非包罗万象,含有任何元素的集合,它仅仅含有我们所要研究的问题中所涉及的所有元素,如研究方程实根,全集取为R;研究整数,全集取为Z,同时,要理解补集的定义的 用法.1.交集与并集是集合的两种不同运算,对它们概念的理解要特别注意“且”与“或” 的区别.交集和并集的符号“∩”“∪”既有相同的地方,但又完全不同,不要混淆.
2.对于交集“A∩B={x|x∈A,且x∈B}”,不能简单地认为A∩B中的任一元素都是A与B的公共元素,或者简单地认为A与B的公共元素都属于A∩B,这是因为并非任何两个集合总有公共元素.
3.对于并集“A∪B={x|x∈A,或x∈B}”,不能简单地理解为A∪B是由A的所有元素与B的所有元素组成的集合,这是因为A与B可能有公共元素4.Venn图在研究集合与元素、集合与集合关系中有广泛的应用,它主要体现在用图示帮助我们加强问题的理解,是数形结合在集合中的具体体现,特别是在解决列举法给出的集合运算中应用广泛.
5.解决集合问题,应从元素入手进行分析处理.在顺向思维受阻时,改用逆向思维,可能“柳暗花明”,从这个意义上讲,补集思想具有转换研究对象的功能,这是转化思想的又一体现.祝同学们学习上天天有进步!
2.一般地,由属于集合A且属于集合B的所有元素组成的集合,称为集合A与B的 ,记作 ,即A∩B= .
3.(1)一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为 ,通常记作 .
(2)对于一个集合,由全集U中不属于集合A的所有元素组成的集合称
为集合A相对于全集U的 ,记作 ,
即 .
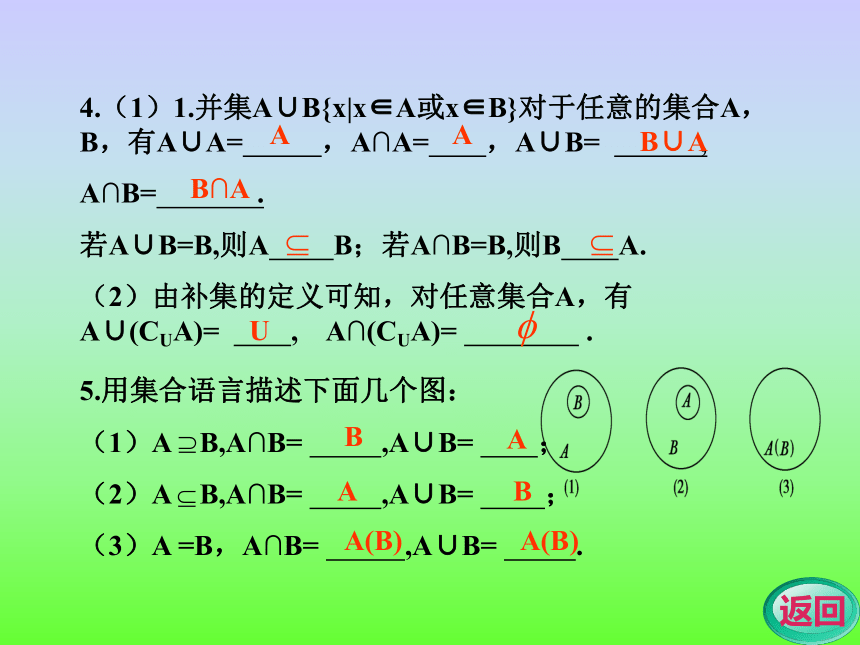
并集A∪B{x|x∈A或x∈B}交集A∩B{x|x∈A,且x∈B}全集U补 集U?4.(1)1.并集A∪B{x|x∈A或x∈B}对于任意的集合A, B,有A∪A= ,A∩A= ,A∪B= ,
A∩B= .
若A∪B=B,则A B;若A∩B=B,则B A.
(2)由补集的定义可知,对任意集合A,有A∪(CUA)= , A∩(CUA)= .5.用集合语言描述下面几个图:
(1)A B,A∩B= ,A∪B= ;
(2)A B,A∩B= ,A∪B= ;
(3)A =B,A∩B= ,A∪B= .BAABA(B)A(B)AAB∪AB∩AU学点一 基本概念的考查已知U={1,2,3,…,8},A={1,2,3,4},B={2,3,4,5}.求:
(1)A∩B; (2)A∪(CUB);
(3)(CUA)∩(CUB); (4)(CUA)∪(CUB)
【分析】由集合的交、并、补概念直接求解. 【解析】 ∵U={1,2,3,…,8},A={1,2,3,4},B={2,3,4,5},
∴CUA={5,6,7,8}, CUB={1,6,7,8}.
∴(1)A∩B={1,2,3,4}∩{2,3,4,5}={2,3,4}.
(2)A∪(CUB)={1,2,3,4}∪{1,6,7,8}={1,2,3,4,6,7,8}.
(3)(CUA)∩(CUB)={5,6,7,8}∩{1,6,7,8}= {6,7,8}.
(4)(CUA)∪(CUB)={5,6,7,8}∪{1,6,7,8}={1,5,6,7,8 }.【评析】集合的简单运算可由基本概念直接求解.已知集合S={x|1
(3)(CSA)∪(CSB); (4)CS(A∩B).解:A∩B={x|3≤x<5}, A∪B={x|2≤x<7},
CSA={x|1
∴M∩P={x|x≥-1,且x≤3}={x|-1≤x≤3}.故应选C.学点二 交 集【分析】由集合的定义,集合M表示方程y2=x+1中x的范围,
集合P表示方程y2=-2(x-3)中x的范围,故应先化简集合M,P.【评析】理解集合的表示形式,掌握其意义,利用交 集定义可解决所给问题.
已知集合M={x|y2=x+1},P={x|y2=-2(x-3)},那么M∩P=( )
A. {(x,y)x= ,y=± } B.{x|-1
C设集合A={(x,y)|2x+y=1,x,y∈R},B={(x,y)|a2x+2y=a,x,y∈R},
若A∩B=?,求a的值.解:集合A,B的元素分别是二元一次方程2x+y=1和a2x+2y=a的解,因为两方程的公共解集A∩B=?,所以方程组无解.
列方程组 得(4-a2)x=2-a
则 即a=-2.
学点三 并 集设A={4,5,6,8},B={3,5,7,8},下列集合中与A∪B相等的集合是( )
A.{4,5,6,7,8} B.{3,4,6,7,10,16}
C.{3,4,5,6,7,8,9} D.{3,4,5,6,7,8}【分析】注意到集合A与集合B的并集的定义中:
(1)集合A∪B中的元素必须是集合A或集合B的元素,
(2)集合A∪B包含集合A与集合B中的所有元素.D【评析】在判定或书写集合A与集合B的并集时,既不能遗
漏元素, 也不能增添元素,要严格地理解、掌握并集的定义.
【解析】A.3∈B,但3?{4,5,6,7,8},{4,5,6,7,8}?A∪B;
B.10?A,10?B,16?A,16?B,{3,4,6,7,10,16}≠A∪B;
C.9?A,9?B,A∪B?{3,4,5,6,7,8,9};
D.显然A∪B={3,4,5,6,7,8}.
故应选D.已知A={x|x≤-1或x≥3},B={x|a
故应选C.C学点四 补集与全集设A={0,2,4,6},CUA={-1,-3,1,3},CUB={-1,0,2},求B.【分析】由A∪(CUA)=U确定全集U,则B可求.【解析】∵A={0,2,4,6},CUA={-1,-3,1,3},
∴U={-3,-1,0,1,2,3,4,6},
又∵CUB={-1,0,2},∴B={-3,1,3,4,6}.【评析】解决与补集有关的问题时,应明确全集是什么,
同时注意补集的有关性质:CU?=U,CUU=?,CU(CUA)=A等.设全集U={2,3,a2+2a-3},A={|2a-1|,2},且CUA={5},求实数a的值.解:∵CUA={5},∴5∈U,且5?A.
∴a2+2a-3=5,即a=2或a= -4.
当a=2时,|2a-1|=3,这时A={3,2},U={2,3,5}.
∴CUA={5},适合题意.∴a=2.
当a=-4时,|2a-1|=9,这时A={9,2},U={2,3,5},A?U,
∴CUA无意义,故a=-4应舍去.
综上所述可知a=2.学点五 交集的应用已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},
若A∪B=A,求实数m的取值范围.【分析】由A∪B=A得A?B,故应从B?A入手讨论,
但考虑到B是A的子集,因此,不要忘记B=?的情况.【解析】由题意,A∪B=A,∴B?A.
(1)若B=?,则m+1>2m-1,即m<2,
此时总有A∪B=A∪?=A成立.
(2)若B≠?,则
解得2≤m≤3.
综合(1)(2)知,m的取值范围是{m|m<2}∪{m|2≤m≤3}={m|m≤3}.
【评析】由A∪B=A可得B?A,而B?A包括两种情况,
即B=?和B≠?.本题常犯的错误是把
B=?漏掉而只讨论B≠?这一种情况.设集合A={a2, a+1,-3},B={a-3,2a-1,a2+1},A∩B={-3},求实数a的值.解:∵A∩B={-3},∴-3∈B.
∴a-3= -3或2a-1= -3,
∴a=0或a= -1.
当a=0时,A={0,1,-3},B={-3,-1,1},此时A∩B={1,-3},与A∩B={-3}矛盾,故舍去.
当a= -1时,A={1,0,-3},B={-4,-3,2},满足A∩B={-3},
∴a= -1.学点六 Venn图的应用【分析】关于集合的交、并、补的问题,通常可以由分析法
找出集合中一定有或一定没有的元素,对它们逐一检验;
或利用Venn图,把元素一一放入图中相应位置,从而写出所
求集合.【解析】解法一:利用Venn图,在图中
标出各个元素的相应位置,可以直接写
出A与B,A={2,3,5,7},B={1,2,9}.若集合U={x|x是小于10的正整数},A?U,B?U,且(CUA)∩B={1,9},
A∩B={2},(CUA)∩(CUB)={4,6,8},试求A与B.解法二:∵A∩B={2},(CUA)∩B={1,9},
∴B=(A∩B)∪[(CUA)∩B]={1,2,9}.
∵A∪B=CU[(CUA)∩(CUB)]={1,2,3,5,7,9},
又∵B={1,2,9},A∩B={2},∴A={2,3,5,7}.【评析】事实上,在解决这类问题时,将Venn图的使用与分
析法相结合更准确简捷.设A,B都是不超过8的正整数组成的全集U的子集A∩B={3},
(CUA)∩(CUB)={1,8},(CUA)∩B={4,6},求集合A,B.解:U={1,2,3,4,5,6,7,8},在Venn图中将1,2,3,4,5,6,7,8分别填入到相应的位置中去,则由A∩B={3},CUA∩CUB={1,8},
(CUA)∩B={4,6}得A∩(CUB)={2,5,7}.
∴A={2,3,5,7},B={3,4,6}.学点七 集合运算的应用已知集合S={1,3,x3+3x2+2x},A={1,|2x-1|},如果CSA={0},
则这样的实数x是否存在?若存在,求出x;若不存在,说明理由.【分析】解决此问题的关键是正确理解CSA={0}的意义,
它有两层含义,即0∈S,但0?A,这样解题思路就清楚了.【评析】解答此题时,我们由CSA={0}求出x1=0,x2=-1,x3=-2之后,验证其是否符合题目的隐含条件A?S是必要的,否则就会误认为x1=0或x3=-2也是所求的实数x,从而得出错误的结论.集合概念及其基本理论是近、现代数学的最基础的内容之一,学好这部分知识的目的之一就是在于应用. 因此,一定要学会读懂集合的语言和符号,并能运用集合的观点研究、判断和处理简单的实际问题.解:(1)如A={1,2,3},B={2,3,4},则A-B={1}.
(2)不一定相等,由(1)知B-A={4},而A-B={1},B-A≠A-B.再如A={1,2,3},B={1,2,3},A-B=?,B-A=? ,此时A-B=B-A.故A-B与B-A
不一定相等.
(3)因为A-B={x|x≥6}, B-A={x|-6
设A,B是两个非空集合,定义A与B的差集为A-B={x|x∈A且x?B}.
(1)试举出两个数集A,B,求它们的差集;
(2)差集A-B与B-A是否一定相等?并说明你的理由;
(3)已知A={x|x>4},B={x||x|<6},求A-(A-B)及B-(B-A),由此
你可以得到什么更一般的结论?(不必证明)1.在解题时如何用好集合语言?
解集合问题,不仅仅是运用集合语言,更重要的是明确集合语言所蕴含的真实的数学含义,集合语言的转换过程,实质就是在进行数学问题的等价转换时,向着我们熟悉的能够解决的问题转化.
2.在学习时应注意什么问题?
(1)对于交集、并集、全集、补集等概念的理解,要注意教材中的实例和Venn图的直观作用.
(2)要善于将三者进行比较记忆,找出它们之间的联系与区别.(3)注意在集合运算中,运用Venn图,借助于数轴等几何方法直观理解.
(4)学会集合语言的运用,并逐渐学会用集合的观点研究事物的内涵与外延.
3.怎样理解全集和补集?
全集并非包罗万象,含有任何元素的集合,它仅仅含有我们所要研究的问题中所涉及的所有元素,如研究方程实根,全集取为R;研究整数,全集取为Z,同时,要理解补集的定义的 用法.1.交集与并集是集合的两种不同运算,对它们概念的理解要特别注意“且”与“或” 的区别.交集和并集的符号“∩”“∪”既有相同的地方,但又完全不同,不要混淆.
2.对于交集“A∩B={x|x∈A,且x∈B}”,不能简单地认为A∩B中的任一元素都是A与B的公共元素,或者简单地认为A与B的公共元素都属于A∩B,这是因为并非任何两个集合总有公共元素.
3.对于并集“A∪B={x|x∈A,或x∈B}”,不能简单地理解为A∪B是由A的所有元素与B的所有元素组成的集合,这是因为A与B可能有公共元素4.Venn图在研究集合与元素、集合与集合关系中有广泛的应用,它主要体现在用图示帮助我们加强问题的理解,是数形结合在集合中的具体体现,特别是在解决列举法给出的集合运算中应用广泛.
5.解决集合问题,应从元素入手进行分析处理.在顺向思维受阻时,改用逆向思维,可能“柳暗花明”,从这个意义上讲,补集思想具有转换研究对象的功能,这是转化思想的又一体现.祝同学们学习上天天有进步!
