3.4平行四边形的性质（1）

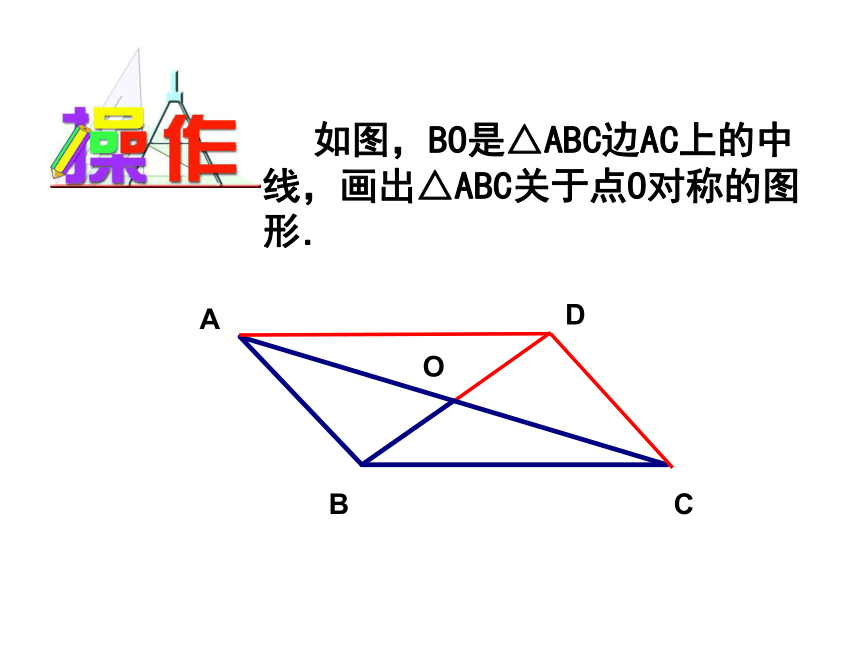
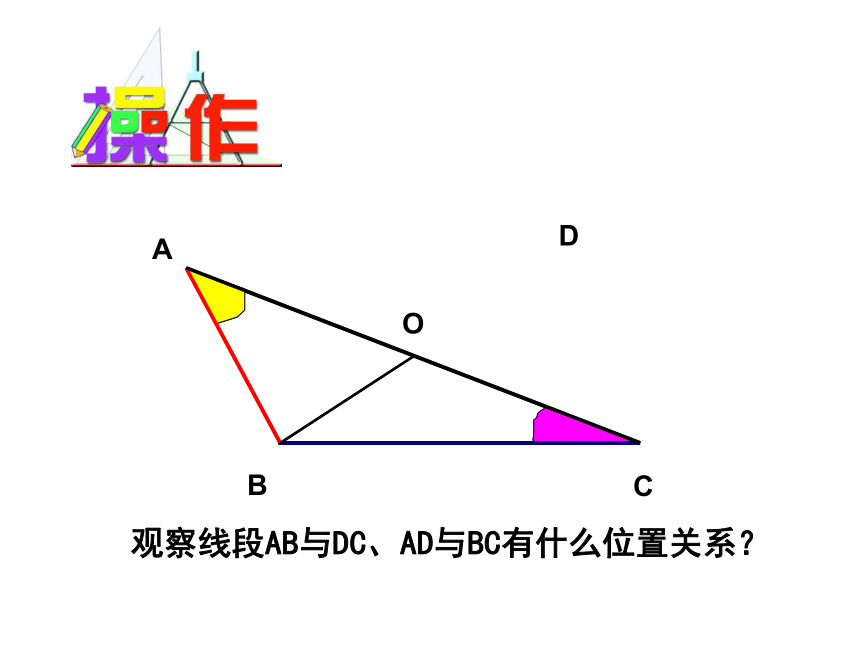
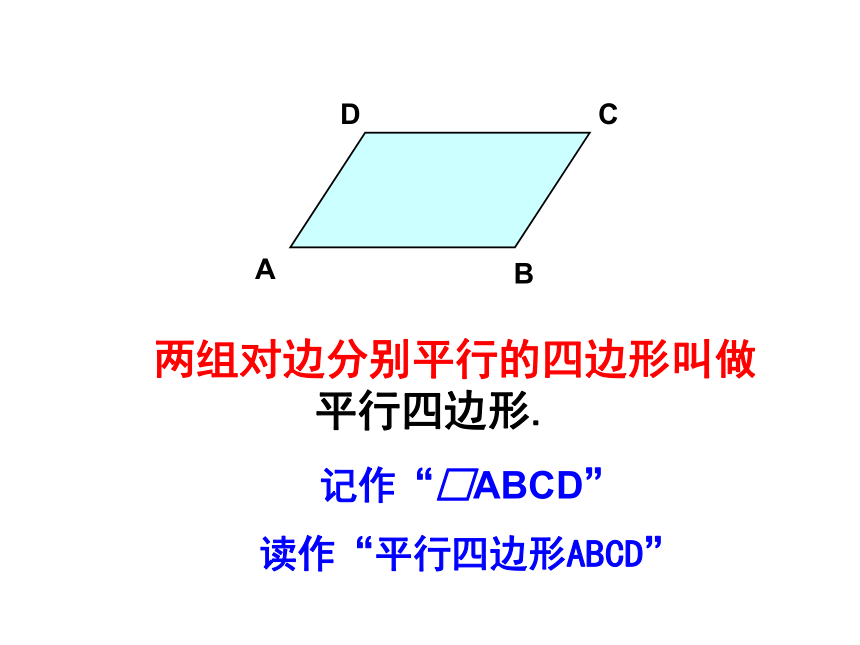
课件19张PPT。3.4平行四边形（1）ABCO 如图，BO是△ABC边AC上的中线，画出△ABC关于点O对称的图形． DABCOD观察线段AB与DC、AD与BC有什么位置关系？ 两组对边分别平行的四边形叫做平行四边形.DABC记作“□ABCD”
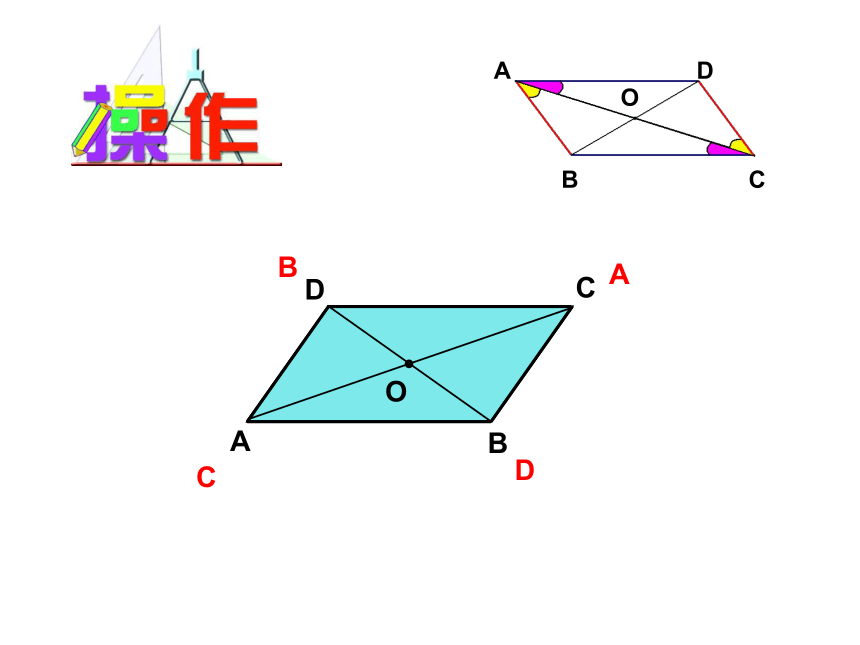
读作“平行四边形ABCD”ABCDOO平行四边形的性质： 平行四边形的对边相等平行四边形的对角相等平行四边形的对角线
互相平分平行四边形性质（关系）边角对角线∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC∵四边形ABCD是平行四边形，
∴ ∠BAD=∠BCD，∠ABC=∠ADC
∵四边形ABCD是平行四边形，
∴ A0=0C，OD=OB （平行四边形的对边相等 ）（平行四边形的对角相等 ）（平行四边形的对角线互相平分）O1.如图，□ABCD中，AC、BD相交于点O，则图中
①相等的线段有 ；
②全等三角形共有 对；
③与∠ABC互补的角有 个，它们是 .
2.考察下列关于四边形的特征：
①对角相等；②对角互补；③邻角互补；④内角和为360°；⑤外角和为360°；⑥有一个角为45°.其中平行四边形一定具有的是 . 重点透视：AB=CD，AD=BC，OA=OC，OB=OD42∠BAD，∠BCD① ，③， ④， ⑤ 如图，点D、E、F分别在边AC、AB、BC上，且AB∥DF，BC∥DE，CA∥EF. 图中有几个平行四边形?将它们用符号表示出来. 说明四边形ADFE是平行四边形的理由.解：图中共有3个平行四边形，
分别是：□ADFE、□EDFB、□EDCF.∵AB ∥DF ，CA∥EF
∴四边形ADFE是平行四边形.
（两组对边分别平行的四边形是平行四边形）
同理，得：四边形EDFB、四边形EDCF也是平行四边形.
1. 在□ABCD中，若周长是30，AB：BC=2：3，
则AD= ，CD= ．
2.已知□ABCD中， ∠A =50°，则∠B = °，
∠C= °,∠D = °.
3.如图，□ABCD的对角线交于点O, BC=7，AC=10，BD=6. 则△AOD的周长= . 如图，在□ABCD中，AD⊥BD,
AC=10cm，BD=6cm. 求AD的长. 你能解决吗？ 如图，在□ABCD中，E是BC上一点，AB=AE，AE的延长线交DC的延长线于点F.若∠F=62°，求∠BAE和∠D的度数. （3题图）课堂检测5分钟 1、 ABCD中，∠A=3 ∠B, 则∠C= ，∠D= .

2、 ABCD中, ∠A:∠B=2:1，则∠C = ,∠D= .

3、平行四边形的周长是40cm，两邻边的比是3:2，则较长边长为 .
45°135°120°60°12cm 4、 ABCD中，已知AB，BC，CD三条边的长度分别为(x+3)cm,(x－4)cm,16cm,这个平行四边形的周长是 .

5、在 ABCD中，∠B的平分线分对边所成的两条线段长分别是3cm，和4cm，则 ABCD的周长是（ ）
巩固与提高50cm20cm或22cm
通过本节课的学习，你对平行四边形有哪些新的认识？有哪些收获与体会？课堂感悟 已知：如图，□ABCD的对角线AC、BD相交
于点O，直线EF过点O与AD、BC相交于点E、F，
①请说明： OE=OF．
②若直线EF与DC、BA的延长线相交于点F、E，
上述结论是否还成立？若成立，请说明理由.
拓展延伸：