新课标A4-4曲线的极坐标方程
图片预览






文档简介
课件15张PPT。简单曲线的极坐标方程榆树市弓棚高级中学校复习提问:1、在直角坐标系中,曲线的方程是怎样定义的? 在直角坐标平面上,曲线可以用 x、y 的二元方程F(x,y)=0来表示,这种方程称为曲线的直角坐标方程。2、求曲线方程的步骤是什么? (1)、建立适当的坐标系,用有序的实数对(X,Y)表示曲线一点M的坐标;(2)、写出适合条件P的点M的集合p={M︱P(M)};(3)、用坐标表示条件P(M),列出方程f(x,y)=0;(4)、化方程f(x,y)=0为最简形式; (5)、说明以化简后的方程的解为坐标的点都在曲线上。 探究:半径为 a 的圆的圆心在C(a,0)(a>0),你能用一个等式表示圆上任意一点的极坐标(ρ,θ)满足的条件吗?如图所示,|OP|=|OA|cos∠POA设P(ρ,θ)为圆上任意一点,由于OP⊥AP即 ρ=2acosθ|OA|=2a,∠POA=θ则这个等式就是圆上任意一点的 极坐标(ρ,θ)满足的条件。曲线的极坐标方程 在极坐标系中,如果平面曲线C上任意一点的极坐标中至少有一个满足方程f(ρ,θ )=0,并且坐标适合方程 f(ρ,θ )=0 的点都在曲线C上,那么方程 f(ρ,θ )=0叫做曲线C的极坐标方程。 类似于曲线直角坐标方程的求法,可以求曲线的极坐标方程。 例1:已知圆O的半径为r,建立怎样的极坐标系,可以使圆的极坐标方程更简单?设M (ρ,θ)为圆上任意一点,
则︱MO︳=r,即
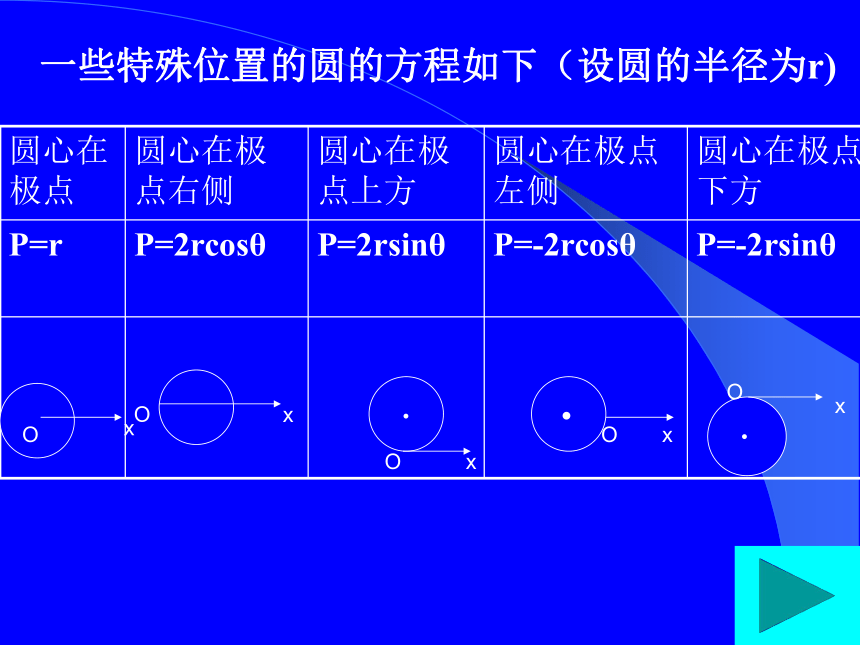
Ρ=r解:以圆心O为极点,射线OX为极轴建立极坐标系一些特殊位置的圆的方程如下(设圆的半径为r)xO·. 探究:如图,直线L经过极点,从极轴到直线L的角是 ,求直线L的极坐标方程。N 以极点O为分界点,直线L上点的极坐标分成射线OM、射线ON两部分。射线OM上任意一点的极角都是 ,因此射线OM的极坐标方程是θ= (ρ≥0) 射线ON上任意一点的极角都是 ,因此射线ON的极坐标方程是θ= (ρ≥0)
因此,直线L的方程可以用θ=
和θ= 表示。如果ρ取全体实数,那么极坐标方程θ= 或θ= 例2 求过点A(2,0)且垂直于极轴的直线的极坐标方程。解:如图所示,在所求直线 l 上任取一点P(ρ,θ),连结OP,则|OP|= ρ,∠POA=θ在Rt△POA中,由于OA/OP=cosθ,所以 2/ρ=cosθ,所以 ρcosθ=2为所求直线的极坐标方程。求曲线的极坐标方程的步骤是:(1)、建立适当的极坐标系,用( ρ,θ )表示曲线上任意一点M的坐标;(2)、寻求点M所满足条件;(3)、用 ρ,θ 表示上述条件,列出方程;(4)、如果所得的方程比较复杂,那么还需要化简方程。课堂练习1、下列方程各表示什么曲线?(1)、Y=K (K为常数), 答:_________;(3)、ρ = 8 , 答:______________;(4)、 = (ρ∈R), 答:______________;θ直线圆直线(2)、X=K (K为常数), 答:_________;直线特别地 我们知道,在直角坐标系中,x=k(k为常数)表示一条平行于y轴的直线;y=k(k为常数)表示一条平行于x轴的直线。 我们可以证明(具体从略),在极坐标系中, ρ =k(k为常数,k>0 )表示圆心在极点、半径为k的圆; θ=k(k为常数 , ρ∈R)表示极角为k的一条直线(过极点)。2、求圆心在C(r,π/2)、半径为r的圆的极坐标方程?解:如图所示,由题意可知,所求圆的圆心在垂直于极轴且位于极轴上方的射线上,而圆周经过极点。设圆与垂直于极轴的射线的另一交点为A,则A点的极坐标为(2r, π /2)。设圆上任意一点为P(ρ,θ),连结PA,则|OP|=ρ,∠POx=θ在Rt△POA中,由于cos∠POA=|OP|/|OA|,所以所以 ρ=2rsinθ为所求圆的极坐标方程。小 结 在极坐标系中,求曲线的极坐标方程与在直角坐标系中求曲线的直角坐标方程的方法是类似的。 在求曲线的极坐标方程时,所取的动点M ( ρ,θ ) 要具有任意性,找出用已知条件表示 ρ,θ 之间的关系式是关键。
则︱MO︳=r,即
Ρ=r解:以圆心O为极点,射线OX为极轴建立极坐标系一些特殊位置的圆的方程如下(设圆的半径为r)xO·. 探究:如图,直线L经过极点,从极轴到直线L的角是 ,求直线L的极坐标方程。N 以极点O为分界点,直线L上点的极坐标分成射线OM、射线ON两部分。射线OM上任意一点的极角都是 ,因此射线OM的极坐标方程是θ= (ρ≥0) 射线ON上任意一点的极角都是 ,因此射线ON的极坐标方程是θ= (ρ≥0)
因此,直线L的方程可以用θ=
和θ= 表示。如果ρ取全体实数,那么极坐标方程θ= 或θ= 例2 求过点A(2,0)且垂直于极轴的直线的极坐标方程。解:如图所示,在所求直线 l 上任取一点P(ρ,θ),连结OP,则|OP|= ρ,∠POA=θ在Rt△POA中,由于OA/OP=cosθ,所以 2/ρ=cosθ,所以 ρcosθ=2为所求直线的极坐标方程。求曲线的极坐标方程的步骤是:(1)、建立适当的极坐标系,用( ρ,θ )表示曲线上任意一点M的坐标;(2)、寻求点M所满足条件;(3)、用 ρ,θ 表示上述条件,列出方程;(4)、如果所得的方程比较复杂,那么还需要化简方程。课堂练习1、下列方程各表示什么曲线?(1)、Y=K (K为常数), 答:_________;(3)、ρ = 8 , 答:______________;(4)、 = (ρ∈R), 答:______________;θ直线圆直线(2)、X=K (K为常数), 答:_________;直线特别地 我们知道,在直角坐标系中,x=k(k为常数)表示一条平行于y轴的直线;y=k(k为常数)表示一条平行于x轴的直线。 我们可以证明(具体从略),在极坐标系中, ρ =k(k为常数,k>0 )表示圆心在极点、半径为k的圆; θ=k(k为常数 , ρ∈R)表示极角为k的一条直线(过极点)。2、求圆心在C(r,π/2)、半径为r的圆的极坐标方程?解:如图所示,由题意可知,所求圆的圆心在垂直于极轴且位于极轴上方的射线上,而圆周经过极点。设圆与垂直于极轴的射线的另一交点为A,则A点的极坐标为(2r, π /2)。设圆上任意一点为P(ρ,θ),连结PA,则|OP|=ρ,∠POx=θ在Rt△POA中,由于cos∠POA=|OP|/|OA|,所以所以 ρ=2rsinθ为所求圆的极坐标方程。小 结 在极坐标系中,求曲线的极坐标方程与在直角坐标系中求曲线的直角坐标方程的方法是类似的。 在求曲线的极坐标方程时,所取的动点M ( ρ,θ ) 要具有任意性,找出用已知条件表示 ρ,θ 之间的关系式是关键。
