反比例函数复习课件
图片预览



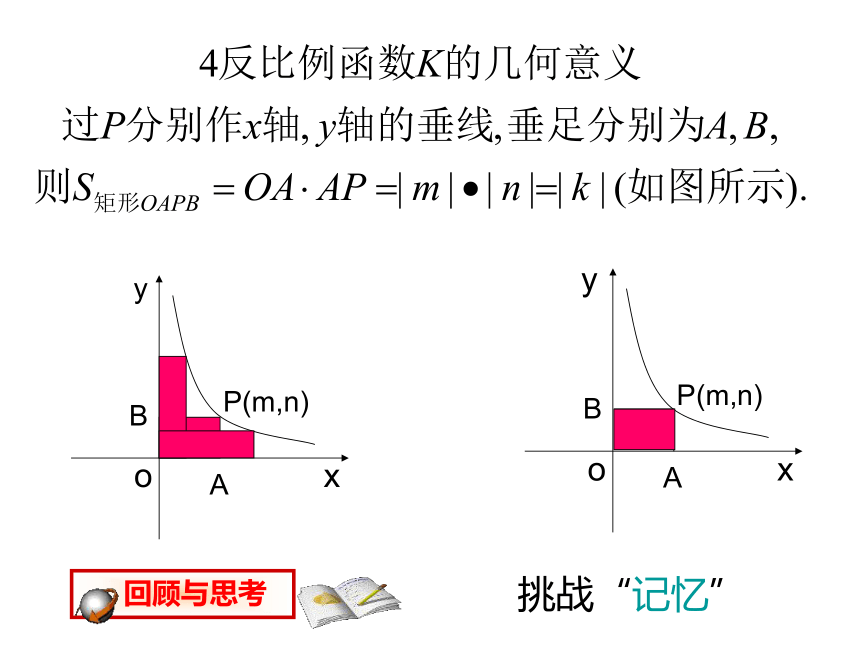
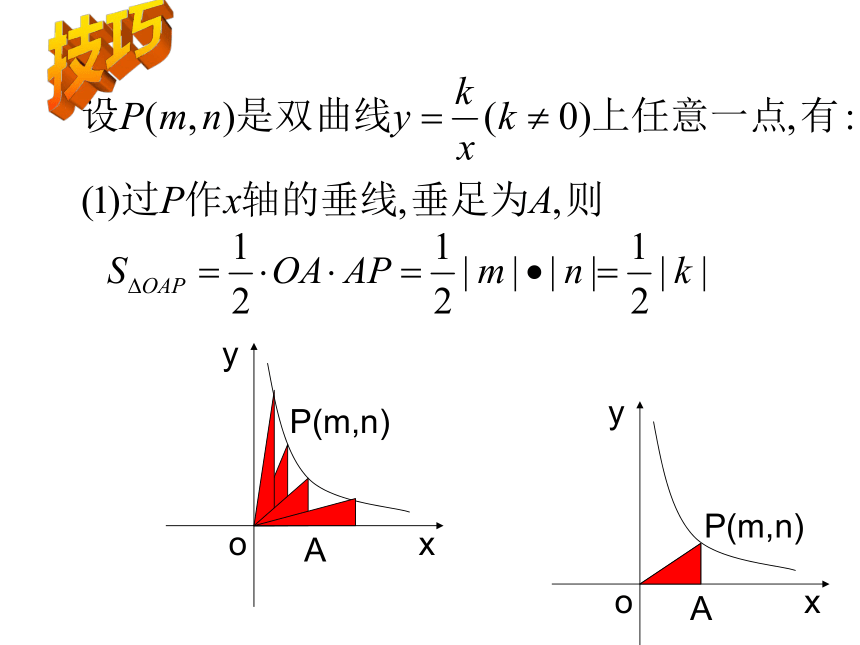



文档简介
课件34张PPT。反比例函数复习课教学目标:
1.通过回顾与思考进一步掌握反比例函数的概念,图象和性质.
2.逐步提高从函数图象中获取信息的能力,建立反比例函数模型并能利用图象解决实际问题,体验数形结合的思想方法.
3.培养学生归纳,整理等能力,发展学生的数学应用能力和形象思维能力.挑战“记忆”我反思——我进步
1反比例函数的概念?表达式? 一般地,如果两个变量x,y之间的关系可以表示成 (k是常数,k≠0)的形式,那么称y是x的反比例函数.
反比例函数的自变量x≠0
也可以写成XY=K(K≠0)的形式.
也可以写成y=kx-1(K≠0)的形式.
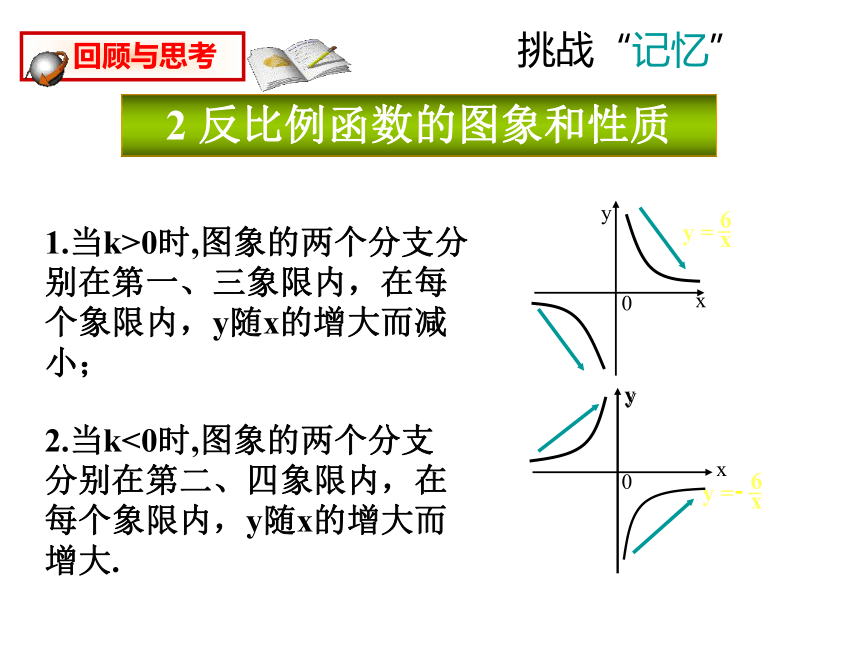
2 反比例函数的图象和性质1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,y随x的增大而减小;2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,y随x的增大而增大.
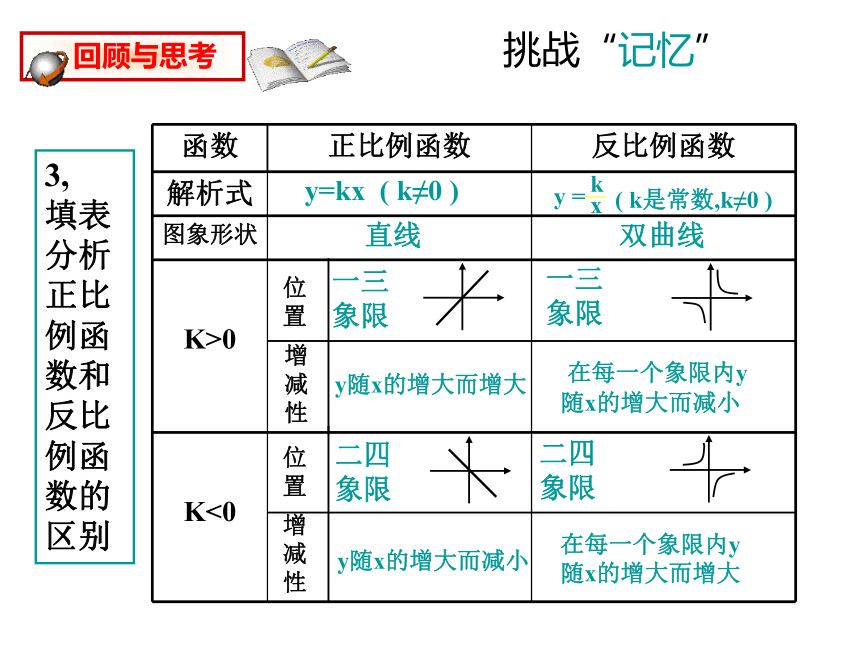
0挑战“记忆”位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 在每一个象限内y随x的增大而减小二四象限二四象限 y随x的增大而减小在每一个象限内y随x的增大而增大
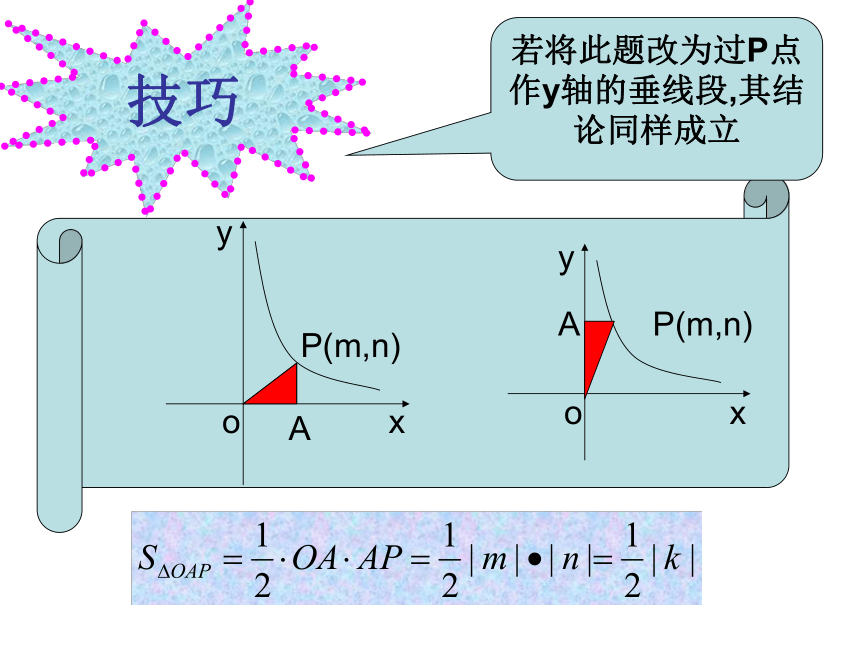
3, 填表分析正比例函数和反比例函数的区别挑战“记忆”挑战“记忆”技巧技巧
若将此题改为过P点作y轴的垂线段,其结论同样成立挑战“记忆”1.反比例函数 的图象是不是轴对称图形?如果是,它有几条对称轴?你能写出对称轴的表达式吗?
y=x y=-x一 透视反比例函数表达式的五种类型1定义型
例1若函数y=(k+1)xk2+3k+1是反比例函数,则此反比例函数的表达式为
解析:由反比例函数的定义,得k2+3k+1=-1且k+1≠0,解得k=-2.故所求反比例的表达式为y=-1/x一.透视反比例函数表达式的五种类型2 一点型
例2,已知反比例函数的图象经过点(-3,1),则该函数的表达式为
解析:设该函数的表达式为y=k/x
∵反比例函数的图象经过点(-3,1)
∴1=k/-3,即k=-3
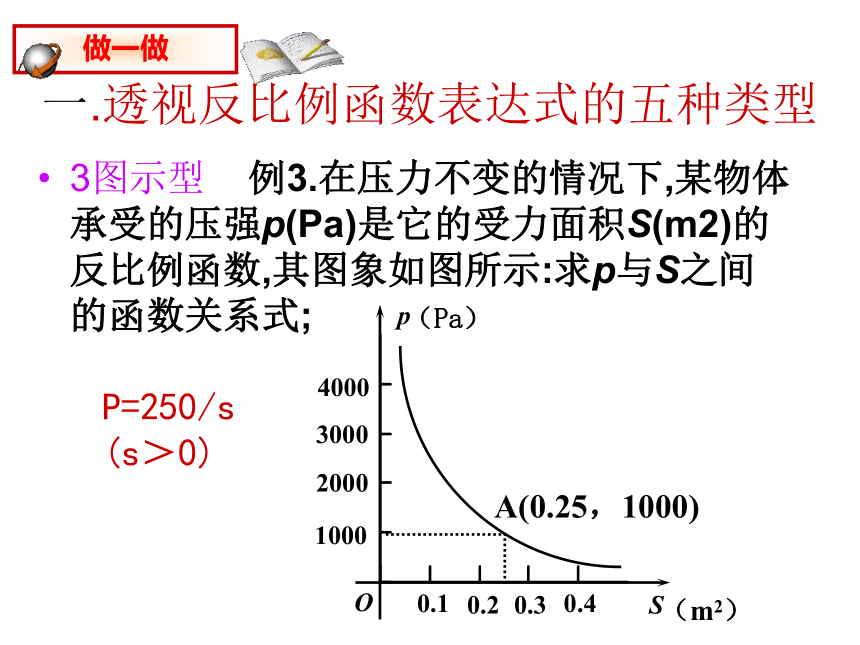
故该函数的表达式为y=-3/x一.透视反比例函数表达式的五种类型3图示型 例3.在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示:求p与S之间的函数关系式;P=250/s(s>0)一.透视反比例函数表达式的五种类型4开放型
例4,写出一个图象位于第二,四象限的反比例函数的解析式 (写出一个符合条件的即可)一 透视反比例函数表达式的五种类型5面积型 如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是 .
二 请“图象”帮忙1人均产量中的数学某村的粮食总产量为a(a为常数),设该村粮食的人均产量为y(吨),人口数为x(人),则y与x之间的函数图象大致是( ). y=a/x (x>0)c精心选一选已知甲,乙两地相距skm,汽车从甲地匀速行驶到乙地.如果汽车每小时耗油量为aL,那么从甲地到乙地的总耗油量y(L)与汽车的行驶速度v(km/h)的函数图象大致是( ).2耗油过程中的数学y=s a/v (s,a是常数,v>0)c在实际问题中
图象就可能只
有一支.3面积计算中的函数知识方法结“网络”已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).2πrh=10π得 h=5/rc 4已知函数y=k/x 的图象如下右图,则y=k x-2 的图象大致是( )xxxxxyyyyyooooo(A)(D)(C)(B)DK>0 , b=-2<0 由k<0可知,两个函数的图象在第二,四象限,故可选(2),(4);再由y=k(x-1)=kx-k得-k>0,即一次函数与y轴的正半轴相交,因此选(2).5观察与发现“慧眼”辩真伪6.已知反比例函数 (k≠0)
当x<0时,y随x的增大而减小,
则一次函数y=kx-k的图象不经过第 象限.k>0k>0 ,-k<0二请“图象”帮忙7.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .y2> y1请“图象”帮忙XY-1y1-2y2o8.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1、y2与y3的大小关系(从大到小)为 .A(-2,y1),B(-1,y2),C(4,y3)y3 >y1>y2请“图象”帮忙9.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .A(x1,y1),B(x2,y2)且x1<0<x2y1 >0>y2请“图象”帮忙xYO12L1ACBDL210,如图 L1是反比例函数y=k/x在第一象限的函数图象,且过点A(2,1),L2与L1关于X轴对称,那么图象L2的函数解析式为 ( ) Y=-2/X(X>0)(2,-1)二 请“图象”帮忙xyY=k1/xY=k2/xY=k3/xABCDEFO11,如图是三个反比例函数y=k1/ x, y=k2/ x, y=k3/ x在X轴上方的图象,由此观察得到k1,k2,k3的大小关系为( )
A. k1>k2>k3 B .k2>k3>k3 C.k3>k2>k1 D.k3>k1>k2C请“图象”帮忙GxyoAC12,如图 ,反比例函数y=2/x的图象与直线y=kx(k>0)相交于A,B两点,AC⊥X轴于点C,则S△AOC=BDF过点B作BD⊥X轴于点D,连接AD,BC,则四边形ADBC的面积为
过点B作BE⊥Y轴于E交AC的延长线于点F,则 △ABF的面积是
144设点A的坐标为(m,n),则点B的坐标为(-m, -n),BF﹦2m,AF﹦2n
S△ABF=1/2 BF AF= 1/2 ×2m×2n=2mn
又点A(m,n)在y=2/x的图象上,所以mn=2 因此S△ABF=2×2=4二 请“图象”帮忙E13,超越自我:二 请“图象”帮忙X(分钟)y(毫克)o6814为了预防流感,学校对教室采用药熏消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例.药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y与x的函数关系式为 ,自变量x的取值范围为 ;药物燃烧后, y与x的函数关系式为 .(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟,学生才能回到室 . (3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?y=3x/40<x≤8y=48/x1.63030二 请“图象”帮忙X(分钟)y(毫克)o68(1)药物燃烧时,y与x的函数关系式为 ,自变量x的取值范围为 ;药物燃烧后, y与x的函数关系式为 .(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟,学生才能回到室 . (3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有 效?为什么?
y=3x/40<x≤8y=48/x1.630303416解:此次消毒有效.因为把y=3分别y=3x/4,y=48/x,求得x=4和x=16,而16-4=12>10,即空气中的含药量不低于3毫克/m3的持续时间为12分钟,大于10分钟的有效时间.二 请“图象”帮忙结束寄语函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
从函数的图象中获取信息的能力是学好数学必需具有的基本素质.祝同学们学习进步!
再见感谢各位老师光临指导!
1.通过回顾与思考进一步掌握反比例函数的概念,图象和性质.
2.逐步提高从函数图象中获取信息的能力,建立反比例函数模型并能利用图象解决实际问题,体验数形结合的思想方法.
3.培养学生归纳,整理等能力,发展学生的数学应用能力和形象思维能力.挑战“记忆”我反思——我进步
1反比例函数的概念?表达式? 一般地,如果两个变量x,y之间的关系可以表示成 (k是常数,k≠0)的形式,那么称y是x的反比例函数.
反比例函数的自变量x≠0
也可以写成XY=K(K≠0)的形式.
也可以写成y=kx-1(K≠0)的形式.
2 反比例函数的图象和性质1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,y随x的增大而减小;2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,y随x的增大而增大.
0挑战“记忆”位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 在每一个象限内y随x的增大而减小二四象限二四象限 y随x的增大而减小在每一个象限内y随x的增大而增大
3, 填表分析正比例函数和反比例函数的区别挑战“记忆”挑战“记忆”技巧技巧
若将此题改为过P点作y轴的垂线段,其结论同样成立挑战“记忆”1.反比例函数 的图象是不是轴对称图形?如果是,它有几条对称轴?你能写出对称轴的表达式吗?
y=x y=-x一 透视反比例函数表达式的五种类型1定义型
例1若函数y=(k+1)xk2+3k+1是反比例函数,则此反比例函数的表达式为
解析:由反比例函数的定义,得k2+3k+1=-1且k+1≠0,解得k=-2.故所求反比例的表达式为y=-1/x一.透视反比例函数表达式的五种类型2 一点型
例2,已知反比例函数的图象经过点(-3,1),则该函数的表达式为
解析:设该函数的表达式为y=k/x
∵反比例函数的图象经过点(-3,1)
∴1=k/-3,即k=-3
故该函数的表达式为y=-3/x一.透视反比例函数表达式的五种类型3图示型 例3.在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示:求p与S之间的函数关系式;P=250/s(s>0)一.透视反比例函数表达式的五种类型4开放型
例4,写出一个图象位于第二,四象限的反比例函数的解析式 (写出一个符合条件的即可)一 透视反比例函数表达式的五种类型5面积型 如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是 .
二 请“图象”帮忙1人均产量中的数学某村的粮食总产量为a(a为常数),设该村粮食的人均产量为y(吨),人口数为x(人),则y与x之间的函数图象大致是( ). y=a/x (x>0)c精心选一选已知甲,乙两地相距skm,汽车从甲地匀速行驶到乙地.如果汽车每小时耗油量为aL,那么从甲地到乙地的总耗油量y(L)与汽车的行驶速度v(km/h)的函数图象大致是( ).2耗油过程中的数学y=s a/v (s,a是常数,v>0)c在实际问题中
图象就可能只
有一支.3面积计算中的函数知识方法结“网络”已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).2πrh=10π得 h=5/rc 4已知函数y=k/x 的图象如下右图,则y=k x-2 的图象大致是( )xxxxxyyyyyooooo(A)(D)(C)(B)DK>0 , b=-2<0 由k<0可知,两个函数的图象在第二,四象限,故可选(2),(4);再由y=k(x-1)=kx-k得-k>0,即一次函数与y轴的正半轴相交,因此选(2).5观察与发现“慧眼”辩真伪6.已知反比例函数 (k≠0)
当x<0时,y随x的增大而减小,
则一次函数y=kx-k的图象不经过第 象限.k>0k>0 ,-k<0二请“图象”帮忙7.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .y2> y1请“图象”帮忙XY-1y1-2y2o8.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1、y2与y3的大小关系(从大到小)为 .A(-2,y1),B(-1,y2),C(4,y3)y3 >y1>y2请“图象”帮忙9.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .A(x1,y1),B(x2,y2)且x1<0<x2y1 >0>y2请“图象”帮忙xYO12L1ACBDL210,如图 L1是反比例函数y=k/x在第一象限的函数图象,且过点A(2,1),L2与L1关于X轴对称,那么图象L2的函数解析式为 ( ) Y=-2/X(X>0)(2,-1)二 请“图象”帮忙xyY=k1/xY=k2/xY=k3/xABCDEFO11,如图是三个反比例函数y=k1/ x, y=k2/ x, y=k3/ x在X轴上方的图象,由此观察得到k1,k2,k3的大小关系为( )
A. k1>k2>k3 B .k2>k3>k3 C.k3>k2>k1 D.k3>k1>k2C请“图象”帮忙GxyoAC12,如图 ,反比例函数y=2/x的图象与直线y=kx(k>0)相交于A,B两点,AC⊥X轴于点C,则S△AOC=BDF过点B作BD⊥X轴于点D,连接AD,BC,则四边形ADBC的面积为
过点B作BE⊥Y轴于E交AC的延长线于点F,则 △ABF的面积是
144设点A的坐标为(m,n),则点B的坐标为(-m, -n),BF﹦2m,AF﹦2n
S△ABF=1/2 BF AF= 1/2 ×2m×2n=2mn
又点A(m,n)在y=2/x的图象上,所以mn=2 因此S△ABF=2×2=4二 请“图象”帮忙E13,超越自我:二 请“图象”帮忙X(分钟)y(毫克)o6814为了预防流感,学校对教室采用药熏消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例.药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y与x的函数关系式为 ,自变量x的取值范围为 ;药物燃烧后, y与x的函数关系式为 .(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟,学生才能回到室 . (3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?y=3x/40<x≤8y=48/x1.63030二 请“图象”帮忙X(分钟)y(毫克)o68(1)药物燃烧时,y与x的函数关系式为 ,自变量x的取值范围为 ;药物燃烧后, y与x的函数关系式为 .(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟,学生才能回到室 . (3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有 效?为什么?
y=3x/40<x≤8y=48/x1.630303416解:此次消毒有效.因为把y=3分别y=3x/4,y=48/x,求得x=4和x=16,而16-4=12>10,即空气中的含药量不低于3毫克/m3的持续时间为12分钟,大于10分钟的有效时间.二 请“图象”帮忙结束寄语函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
从函数的图象中获取信息的能力是学好数学必需具有的基本素质.祝同学们学习进步!
再见感谢各位老师光临指导!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
