寿春中学九年级(上)二次函数与反比例函数测试卷
文档属性
| 名称 | 寿春中学九年级(上)二次函数与反比例函数测试卷 |  | |
| 格式 | rar | ||
| 文件大小 | 84.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-31 20:19:00 | ||
图片预览

文档简介
合肥寿春中学九年级(上)二次函数与反比例函数测试卷
班级 学号 姓名 成绩
一.选择题(每题4分,共40分)
1、下列函数中,是二次函数的是…………………………………………………………………( )
A、 B、 C、 D、
2、已知抛物线的解析式为y=(x-2)2+1,则抛物线与y轴交点的坐标是…………………( )
A、(0,1) B、(2,1) C、(0,-1) D、(0,5)
3、函数的图象与轴有交点,则的取值范围是…………………………( )
A. B. C. D.
4、抛物线y=(x-1)(x+3)的对称轴是直线…………………………………………………………( )
A、x=1 B、x=-1 C、 x=2 D、 x=-2
5、若抛物线y=x2+6x+k的顶点在x轴上,则k等于……………………………………………( )
A、0 B、3 C、6 D、9
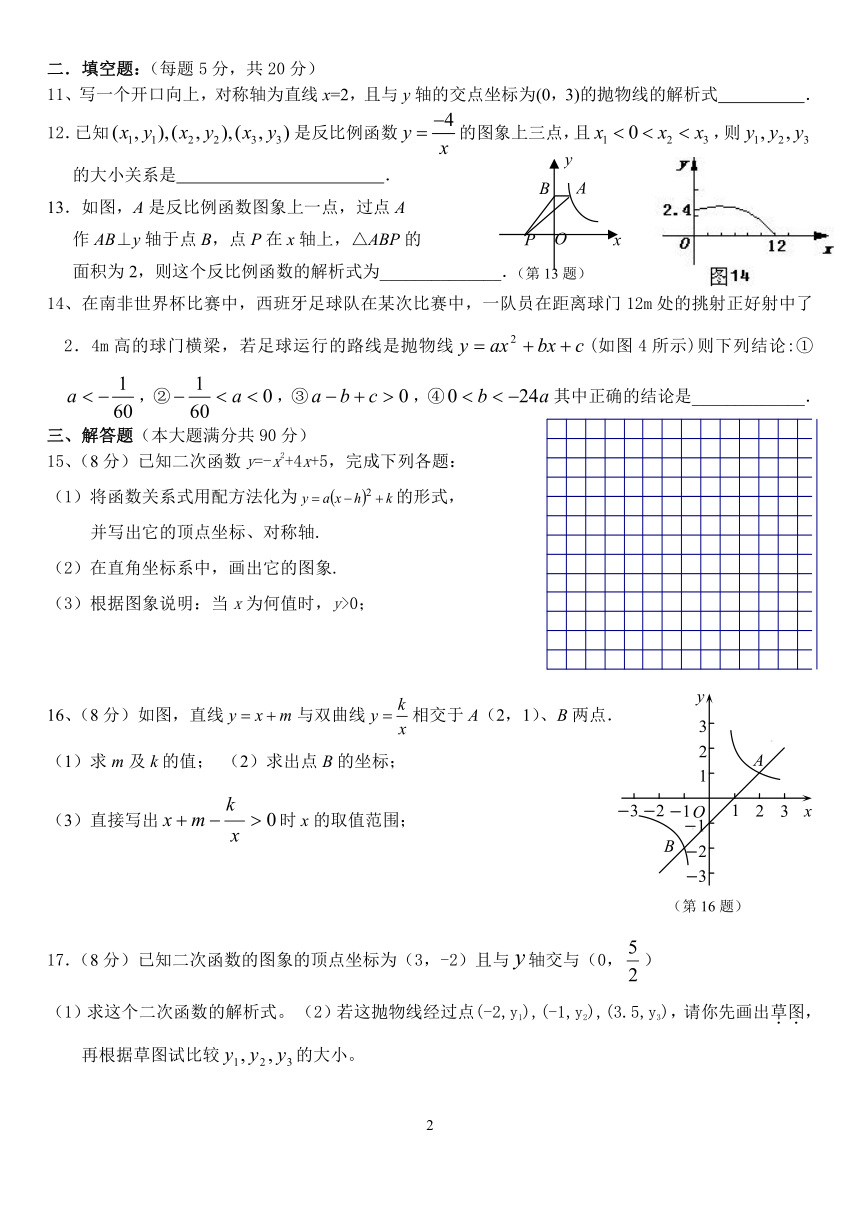
6.反比例函数y=的图象如图所示,则k的值可能是……………… …( )
A.-1 B. C.1 D.2
7、抛物线y=-x2向右平移1个单位,再向上平移2个单位,得到新的图象的二次函数表达式是( )
A、y=-(x-1)2+2 B、 y=-(x+1)2+2 C、y=-(x-1)2-2 D 、y=-(x+1)2-2
8、已知二次函数,
小明利用计算器列出了下表: 那么
方程的一个近似根是…………………………………………………………( )
A.-4.1 B.-4.2 C.-4.3 D.-4.4
9. 抛物线图像如图所示,则一次函数与反比例函数 在同一坐标
系内的图像大致为………………………………………………………………( )
10.如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为,则点D的横坐标最大值为……………………………………………………………………………………………( )
A.-3 B.1 C.5 D.8
二.填空题:(每题5分,共20分)
11、写一个开口向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式 .
12.已知是反比例函数的图象上三点,且,则的大小关系是 .
13.如图,A是反比例函数图象上一点,过点A
作AB⊥y轴于点B,点P在x轴上,△ABP的
面积为2,则这个反比例函数的解析式为______________.
14、在南非世界杯比赛中,西班牙足球队在某次比赛中,一队员在距离球门12m处的挑射正好射中了2.4m高的球门横梁,若足球运行的路线是抛物线(如图4所示)则下列结论:①,②,③,④其中正确的结论是_____________.
三、解答题(本大题满分共90分)
15、(8分)已知二次函数y=-x2+4x+5,完成下列各题:
(1)将函数关系式用配方法化为的形式,
并写出它的顶点坐标、对称轴.
(2)在直角坐标系中,画出它的图象.
(3)根据图象说明:当x为何值时,y>0;
16、(8分)如图,直线与双曲线相交于A(2,1)、B两点.
(1)求m及k的值; (2)求出点B的坐标;
(3)直接写出时x的取值范围;
17.(8分)已知二次函数的图象的顶点坐标为(3,-2)且与轴交与(0,)
(1)求这个二次函数的解析式。 (2)若这抛物线经过点(-2,y1),(-1,y2),(3.5,y3),请你先画出草图,再根据草图试比较的大小。
18.(8分)如图,四边形OABC是面积为4的正方形,函数(x>0)的图象经过点B.
(1)求k的值; (2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、MA′BC.设线段MC′、NA′分别与函数(x>0)的图象交于点E、F,求线段EF所在直线的解析式.
19、(10分)某工厂生产的某种产品按质量分为10个档次。第一档次(最低档次)的产品一天能生产76件,每件利润10元。每提高一个档次,每件利润增加2元,但一天产量减少4件。
1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数解析式;
2)若生产第x档次的产品一天的总利润为1080元,求该产品的质量档次。
20、(10分)二次函数的图象如图所示,根据图象回答:
(1)方程的两个根是 ;
(2)方程ax2+bx+c=4的两个根是 ;
(3)直线y=x+1与抛物线y=ax2+bx+c的交点坐标是 _________.
(4)当x 时, x+1>ax2+bx+c; 当x ____时,x+1< ax2+bx+c
21、(12分)如图,在平面直角坐标系中,正方形AOCB的边长为1,点D在轴的正半轴上,且OD=OB,BD交OC于点E.
(1)求的度数.(2)求过B、O、D三点的抛物线的解析式.(3)求点E的坐标.
22、(12分)甲车在弯路作刹车试验,收集到的数据如下表所示:
速度x(千米/小时) 0 5 10 15 20 25 …
刹车距离y(米) 0 2 6 …
(1)请用上表中的各对数据(x,y)作为点的坐标,在所示的坐 标系中画出甲车刹车距离y(米)与速度x(千米/时)的函数图象,并求函数的解析式.
(2)在一个限速为40千米/时的弯路上,甲、乙两车相向
而行,同时刹车,但还是相撞了.事后测得甲、乙两车的刹车距离分别为12米和10.5米,又知乙车的刹车距离y(米)与速度x(千米/时)满足函数,请你就两车的速度方面分析相撞的原因.
23、(14分)如图,在平面直角坐标系中Rt△AOB的顶点坐标分别,把△绕点逆时针方向旋转°得到△(点转到点的位置),抛物线经过、、三点.
(1)求抛物线的解析式;
(2)若抛物线的顶点为,求△的面积;
(3)在抛物线上是否存在点,使△的面积等于△的面积?若存在,请求出点的坐标;若不存在,请说明理由.
O
A
y
x
1
1
x -4.1 -4.2 -4.3 -4.4
-1.39 -0.76 -0.11 0.56
x
x
x
x
x
(第10题)
O
x
y
(第13题)
A
B
P
x
y
O
A
B
O
x
y
(第16题)
2
1
2
3
-3
-1
-2
1
3
-3
-1
-2
O
y
x
D
E
C
B
A
(第23题)
PAGE
1
班级 学号 姓名 成绩
一.选择题(每题4分,共40分)
1、下列函数中,是二次函数的是…………………………………………………………………( )
A、 B、 C、 D、
2、已知抛物线的解析式为y=(x-2)2+1,则抛物线与y轴交点的坐标是…………………( )
A、(0,1) B、(2,1) C、(0,-1) D、(0,5)
3、函数的图象与轴有交点,则的取值范围是…………………………( )
A. B. C. D.
4、抛物线y=(x-1)(x+3)的对称轴是直线…………………………………………………………( )
A、x=1 B、x=-1 C、 x=2 D、 x=-2
5、若抛物线y=x2+6x+k的顶点在x轴上,则k等于……………………………………………( )
A、0 B、3 C、6 D、9
6.反比例函数y=的图象如图所示,则k的值可能是……………… …( )
A.-1 B. C.1 D.2
7、抛物线y=-x2向右平移1个单位,再向上平移2个单位,得到新的图象的二次函数表达式是( )
A、y=-(x-1)2+2 B、 y=-(x+1)2+2 C、y=-(x-1)2-2 D 、y=-(x+1)2-2
8、已知二次函数,
小明利用计算器列出了下表: 那么
方程的一个近似根是…………………………………………………………( )
A.-4.1 B.-4.2 C.-4.3 D.-4.4
9. 抛物线图像如图所示,则一次函数与反比例函数 在同一坐标
系内的图像大致为………………………………………………………………( )
10.如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为,则点D的横坐标最大值为……………………………………………………………………………………………( )
A.-3 B.1 C.5 D.8
二.填空题:(每题5分,共20分)
11、写一个开口向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式 .
12.已知是反比例函数的图象上三点,且,则的大小关系是 .
13.如图,A是反比例函数图象上一点,过点A
作AB⊥y轴于点B,点P在x轴上,△ABP的
面积为2,则这个反比例函数的解析式为______________.
14、在南非世界杯比赛中,西班牙足球队在某次比赛中,一队员在距离球门12m处的挑射正好射中了2.4m高的球门横梁,若足球运行的路线是抛物线(如图4所示)则下列结论:①,②,③,④其中正确的结论是_____________.
三、解答题(本大题满分共90分)
15、(8分)已知二次函数y=-x2+4x+5,完成下列各题:
(1)将函数关系式用配方法化为的形式,
并写出它的顶点坐标、对称轴.
(2)在直角坐标系中,画出它的图象.
(3)根据图象说明:当x为何值时,y>0;
16、(8分)如图,直线与双曲线相交于A(2,1)、B两点.
(1)求m及k的值; (2)求出点B的坐标;
(3)直接写出时x的取值范围;
17.(8分)已知二次函数的图象的顶点坐标为(3,-2)且与轴交与(0,)
(1)求这个二次函数的解析式。 (2)若这抛物线经过点(-2,y1),(-1,y2),(3.5,y3),请你先画出草图,再根据草图试比较的大小。
18.(8分)如图,四边形OABC是面积为4的正方形,函数(x>0)的图象经过点B.
(1)求k的值; (2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、MA′BC.设线段MC′、NA′分别与函数(x>0)的图象交于点E、F,求线段EF所在直线的解析式.
19、(10分)某工厂生产的某种产品按质量分为10个档次。第一档次(最低档次)的产品一天能生产76件,每件利润10元。每提高一个档次,每件利润增加2元,但一天产量减少4件。
1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数解析式;
2)若生产第x档次的产品一天的总利润为1080元,求该产品的质量档次。
20、(10分)二次函数的图象如图所示,根据图象回答:
(1)方程的两个根是 ;
(2)方程ax2+bx+c=4的两个根是 ;
(3)直线y=x+1与抛物线y=ax2+bx+c的交点坐标是 _________.
(4)当x 时, x+1>ax2+bx+c; 当x ____时,x+1< ax2+bx+c
21、(12分)如图,在平面直角坐标系中,正方形AOCB的边长为1,点D在轴的正半轴上,且OD=OB,BD交OC于点E.
(1)求的度数.(2)求过B、O、D三点的抛物线的解析式.(3)求点E的坐标.
22、(12分)甲车在弯路作刹车试验,收集到的数据如下表所示:
速度x(千米/小时) 0 5 10 15 20 25 …
刹车距离y(米) 0 2 6 …
(1)请用上表中的各对数据(x,y)作为点的坐标,在所示的坐 标系中画出甲车刹车距离y(米)与速度x(千米/时)的函数图象,并求函数的解析式.
(2)在一个限速为40千米/时的弯路上,甲、乙两车相向
而行,同时刹车,但还是相撞了.事后测得甲、乙两车的刹车距离分别为12米和10.5米,又知乙车的刹车距离y(米)与速度x(千米/时)满足函数,请你就两车的速度方面分析相撞的原因.
23、(14分)如图,在平面直角坐标系中Rt△AOB的顶点坐标分别,把△绕点逆时针方向旋转°得到△(点转到点的位置),抛物线经过、、三点.
(1)求抛物线的解析式;
(2)若抛物线的顶点为,求△的面积;
(3)在抛物线上是否存在点,使△的面积等于△的面积?若存在,请求出点的坐标;若不存在,请说明理由.
O
A
y
x
1
1
x -4.1 -4.2 -4.3 -4.4
-1.39 -0.76 -0.11 0.56
x
x
x
x
x
(第10题)
O
x
y
(第13题)
A
B
P
x
y
O
A
B
O
x
y
(第16题)
2
1
2
3
-3
-1
-2
1
3
-3
-1
-2
O
y
x
D
E
C
B
A
(第23题)
PAGE
1
