直角三角形的三边关系(二)
图片预览



文档简介
课件22张PPT。§14.1
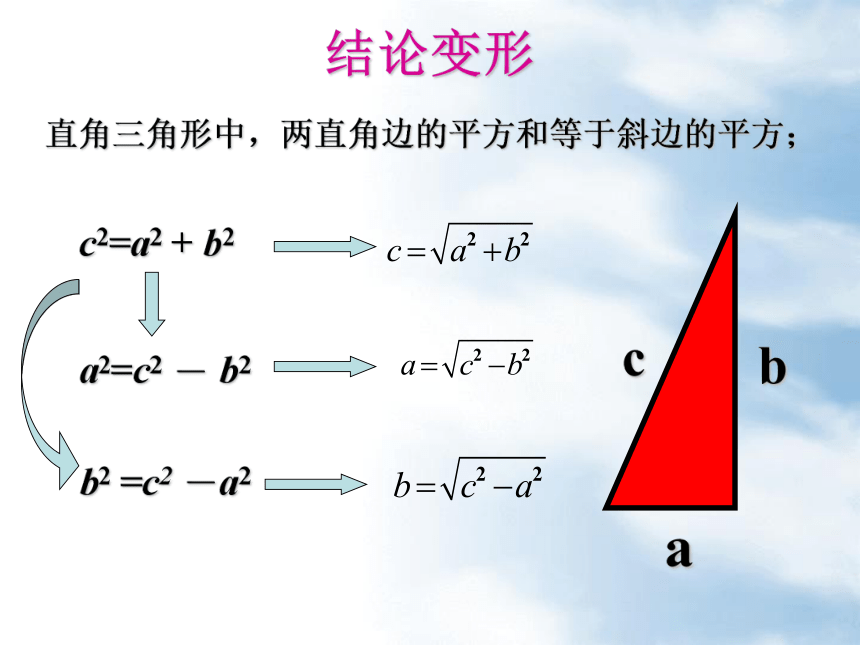
勾股定理的三边关系二 勾股定理 如果直角三角形两直角边分别为a、b,斜边为c,那么 即 直角三角形两直角边的平方和等于斜边的平方.c2=a2 + b2a2=c2 - b2b2 =c2 -a2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 勾股定理曾引起很多人的兴趣,世界上对这个定理的证明方法很多,1940年卢米斯收集了这个定理的370种证明,期中包括大画家达·芬奇和美国总统詹姆士·阿·加菲尔德的证法。到目前为止,已有四百多种证法.
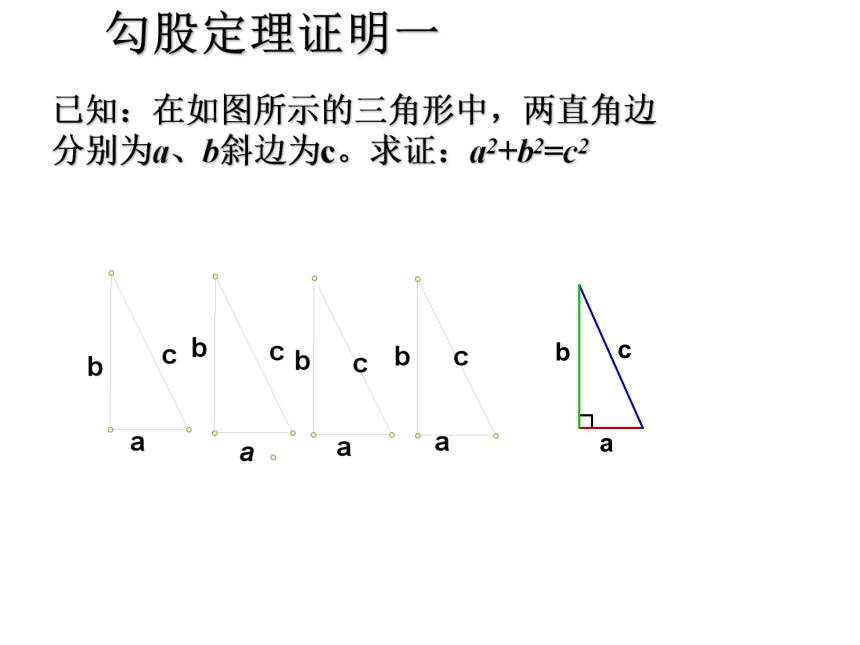
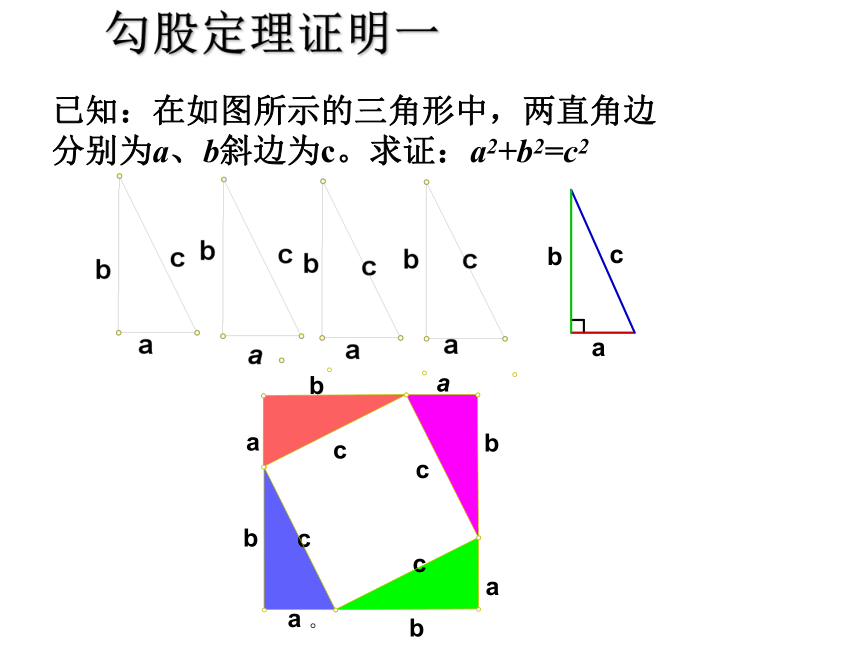
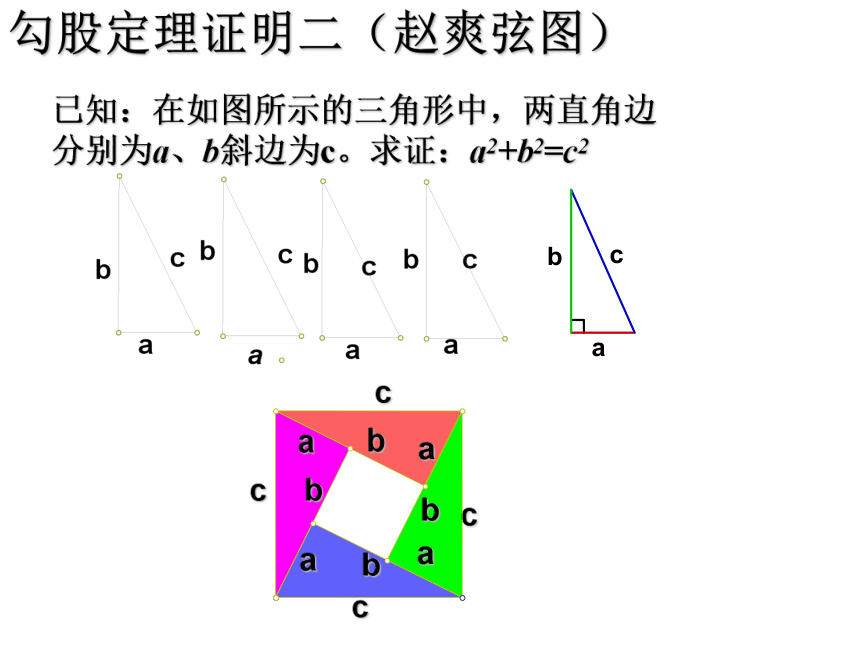
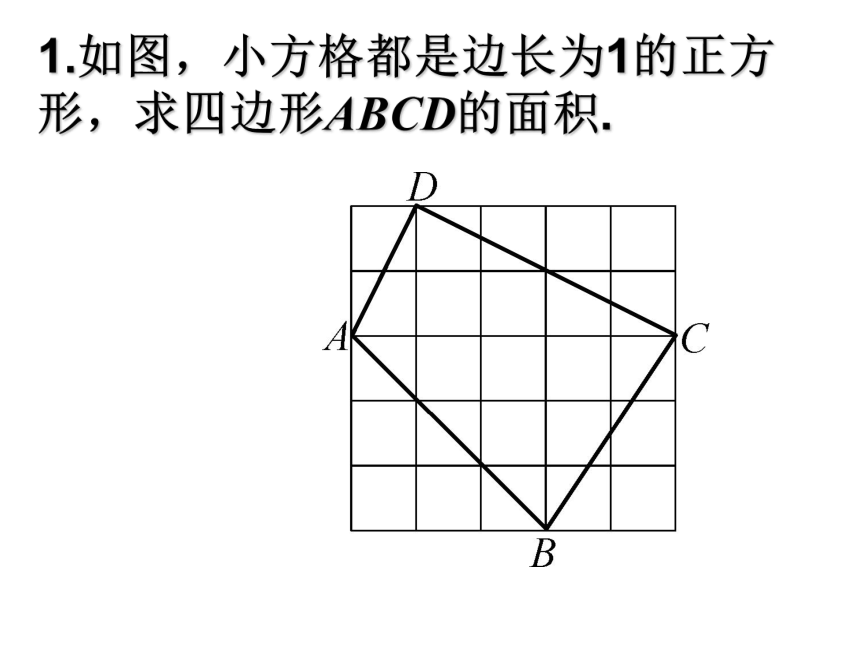
勾股定理证明一已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明一已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明二(赵爽弦图)已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2如图,小方格都是边长为1的正方
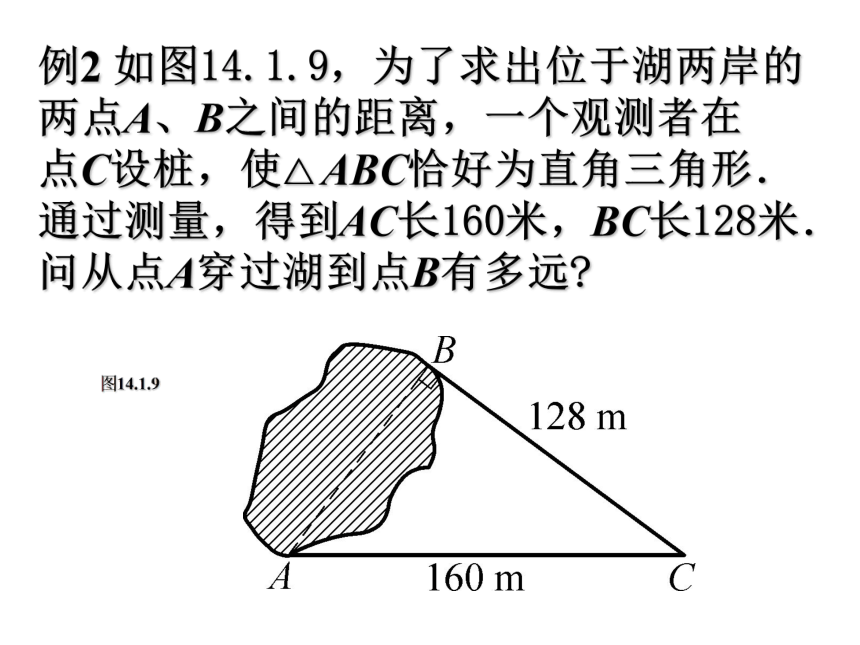
形,求四边形ABCD的面积.例2 如图14.1.9,为了求出位于湖两岸的
两点A、B之间的距离,一个观测者在
点C设桩,使△ ABC恰好为直角三角形.
通过测量,得到AC长160米,BC长128米.
问从点A穿过湖到点B有多远?
图14.1.91.假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏点B的直线距离是多少千米?C 在Rt△ABC中,∠ACB=90°AC=6,BC=8,根据勾股定理,得AB ===10(千米)答:登陆点A到宝藏点B的直线距离是10千米。解:过点B作BC⊥AC于C例 有一张直角三角形纸片,两直角边AC=6cm,
BC=8cm, 将△ABC折叠, 使点B与点A重合,
折痕为DE, 求CD的长.例.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8cm,AD=10cm,
(1)求CF的长;ABCDEF810106x8-x48-x(2)求CE的长美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 证明三:有趣的总统证法伽菲尔德证法
画家的证法达· 芬奇(Leonardo Da Vinci 1452-1519 ).文艺复兴时期卓越的代表人物.
他不仅是一位天才的画家,并且是大数学家、科学家、力学家和工程师.
第一次在数学上使用加减(+、-)符号. 参考:http://yinhe2000.nease.net方法四方法五:下面据传是当年毕达哥拉斯发现勾股定理时做出的证明。 将4个全等的直角三角形拼成边长为(a+b)的正方形ABCD,使中间留下边长c的一个正方形洞.画出正方形ABCD.移动三角形至图2所示的位置中,于是留下了边长分别为a与b的两个正方形洞.则图1和图2中的白色部分面积必定相等,所以c2=a2+b2图1图2 练 习1、图1-1-1是某校的长方形水泥操场,如果一学生要从A角走到C角,至少走( )
A、140 m B、120m
C、100m D、90mCC2、小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高度为( )
A、8 m B、10m C、12m D、14m例1、已知△ABC中, ∠C=90°,BC= a ,
AC= b ,AB=c
已知: a=1, b=2, 求 c;
已知: a =15 , c =17, 求 b;
(3)已知:c=34 , a : b = 8 : 15,求 a ,b.
例
题
分
析1. 求斜边长17厘米、一条直角边长15厘米的
直角三角形的面积.
解: 设另一条直角边长是 x 厘米.
由勾股定理得:
152 + x2 = 172而 x2 = 172 - 152= 289 – 225
= 64∴ x=8 直角三角形的面积是:
(平方厘米)1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=144想一想 小丁的妈妈买了一部34英寸(86厘米)的电视机。小丁量了电视机的屏幕后,发现屏幕只有70厘米长和50厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?想一想:∴售货员没搞错荧屏对角线大约为86厘米∵702+502=7400862=7396 例.甲、乙两位探险者到沙漠进行探险.某日早晨8∶00甲先出发,他以6千米/时的速度向东行走.1时后乙出发,他以5千米/时的速度向北行进.上午10∶00,甲、乙两人相距多远?
勾股定理的三边关系二 勾股定理 如果直角三角形两直角边分别为a、b,斜边为c,那么 即 直角三角形两直角边的平方和等于斜边的平方.c2=a2 + b2a2=c2 - b2b2 =c2 -a2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 勾股定理曾引起很多人的兴趣,世界上对这个定理的证明方法很多,1940年卢米斯收集了这个定理的370种证明,期中包括大画家达·芬奇和美国总统詹姆士·阿·加菲尔德的证法。到目前为止,已有四百多种证法.
勾股定理证明一已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明一已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明二(赵爽弦图)已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2如图,小方格都是边长为1的正方
形,求四边形ABCD的面积.例2 如图14.1.9,为了求出位于湖两岸的
两点A、B之间的距离,一个观测者在
点C设桩,使△ ABC恰好为直角三角形.
通过测量,得到AC长160米,BC长128米.
问从点A穿过湖到点B有多远?
图14.1.91.假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏点B的直线距离是多少千米?C 在Rt△ABC中,∠ACB=90°AC=6,BC=8,根据勾股定理,得AB ===10(千米)答:登陆点A到宝藏点B的直线距离是10千米。解:过点B作BC⊥AC于C例 有一张直角三角形纸片,两直角边AC=6cm,
BC=8cm, 将△ABC折叠, 使点B与点A重合,
折痕为DE, 求CD的长.例.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8cm,AD=10cm,
(1)求CF的长;ABCDEF810106x8-x48-x(2)求CE的长美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 证明三:有趣的总统证法伽菲尔德证法
画家的证法达· 芬奇(Leonardo Da Vinci 1452-1519 ).文艺复兴时期卓越的代表人物.
他不仅是一位天才的画家,并且是大数学家、科学家、力学家和工程师.
第一次在数学上使用加减(+、-)符号. 参考:http://yinhe2000.nease.net方法四方法五:下面据传是当年毕达哥拉斯发现勾股定理时做出的证明。 将4个全等的直角三角形拼成边长为(a+b)的正方形ABCD,使中间留下边长c的一个正方形洞.画出正方形ABCD.移动三角形至图2所示的位置中,于是留下了边长分别为a与b的两个正方形洞.则图1和图2中的白色部分面积必定相等,所以c2=a2+b2图1图2 练 习1、图1-1-1是某校的长方形水泥操场,如果一学生要从A角走到C角,至少走( )
A、140 m B、120m
C、100m D、90mCC2、小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高度为( )
A、8 m B、10m C、12m D、14m例1、已知△ABC中, ∠C=90°,BC= a ,
AC= b ,AB=c
已知: a=1, b=2, 求 c;
已知: a =15 , c =17, 求 b;
(3)已知:c=34 , a : b = 8 : 15,求 a ,b.
例
题
分
析1. 求斜边长17厘米、一条直角边长15厘米的
直角三角形的面积.
解: 设另一条直角边长是 x 厘米.
由勾股定理得:
152 + x2 = 172而 x2 = 172 - 152= 289 – 225
= 64∴ x=8 直角三角形的面积是:
(平方厘米)1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=144想一想 小丁的妈妈买了一部34英寸(86厘米)的电视机。小丁量了电视机的屏幕后,发现屏幕只有70厘米长和50厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?想一想:∴售货员没搞错荧屏对角线大约为86厘米∵702+502=7400862=7396 例.甲、乙两位探险者到沙漠进行探险.某日早晨8∶00甲先出发,他以6千米/时的速度向东行走.1时后乙出发,他以5千米/时的速度向北行进.上午10∶00,甲、乙两人相距多远?
