从数青蛙我们想到了什么
图片预览






文档简介
(共29张PPT)
1 只青蛙1 张嘴,2 只眼睛 4 条腿,扑通1 声跳下水;
2 只青蛙2 张嘴,4 只眼睛8 条腿,扑通2 声跳下水;
3 只青蛙3 张嘴,6 只眼睛12 条腿,扑通3 声跳下水;
n 只青蛙 张嘴, 只眼睛, 条腿,扑
通 声跳下水。
n
2n
4n
n
寻找和探索规律是人类认识自然界和社会的重要环节,找到规律并按规律办事,不仅在数学上而且在人类社会的认识过程中都有非常重要的意义。
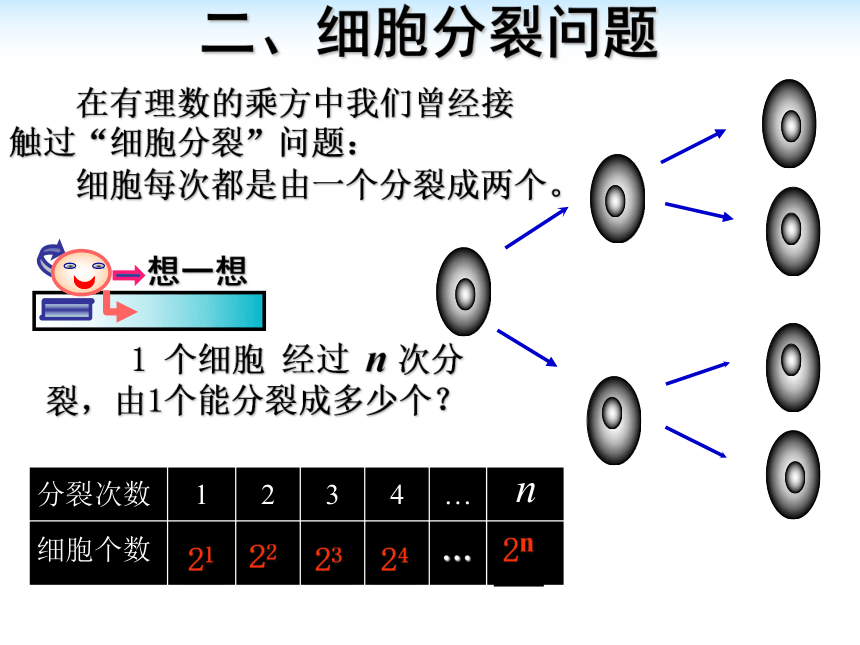
二、细胞分裂问题
细胞每次都是由一个分裂成两个。
在有理数的乘方中我们曾经接触过“细胞分裂”问题:
想一想
1 个细胞 经过 n 次分裂,由1个能分裂成多少个?
分裂次数 1 2 3 4 … n
细胞个数
2
4
8
16
21
22
23
24
2n
…
模 型 “迁移”
你能否找到其它的类似的实际问题,使它与这个问题的条件与结论都对应相同吗?
议 一 议
〖模型1〗
将一根足够长的线段对折,求对折 n 次后线段的总条数。
( 2n条)
〖模型2〗
将一张白纸连续折叠,对折 n 次后的白纸总层数。
( 2n层)
三、折 纸 问 题
将一张白纸对折一次,如图所示折成两层,同时出现一条折痕;如果继续对折,使新折痕与上次的折痕保持平行,想一想,连续对折6次后可以折成多少层,出现几条折痕呢?
如果对折 10 次呢?
如果对折 n 次呢?
对折次数 1 2 3 4 … n
纸张层数
折痕数
2
4
8
16
21
22
23
24
2n
…
1
3
7
15
…
2n-1
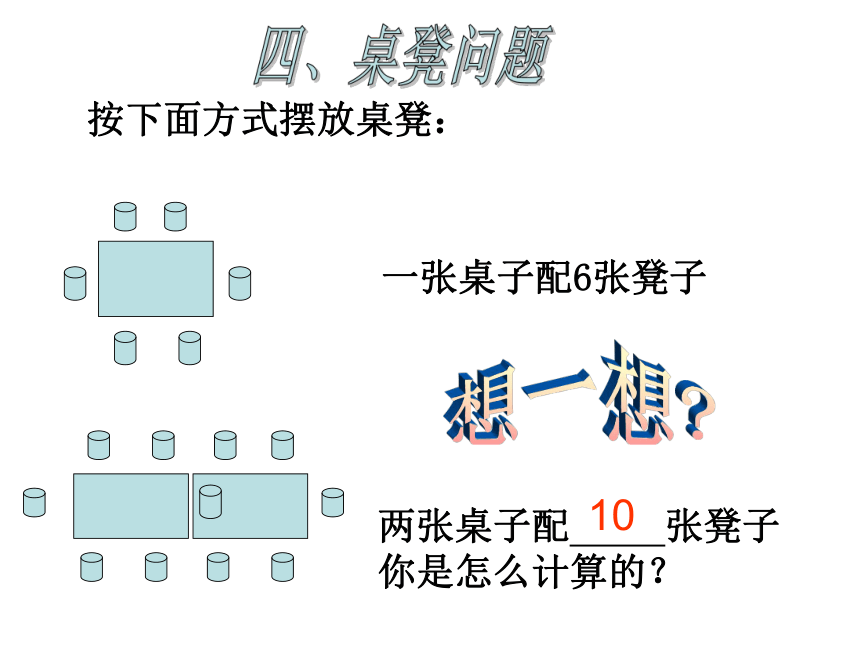
按下面方式摆放桌凳:
一张桌子配6张凳子
两张桌子配 张凳子
你是怎么计算的?
10
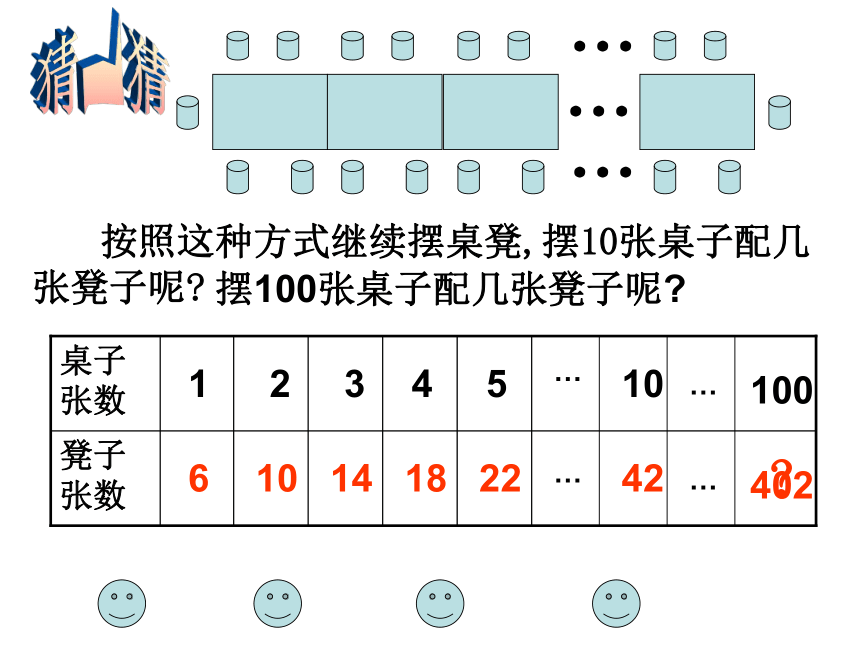
按照这种方式继续摆桌凳,摆10张桌子配几
张凳子呢
…
…
…
摆100张桌子配几张凳子呢
1
6
2
10
3
14
4
18
5
22
凳子张数
桌子张数
10
42
…
…
…
…
100
402
?
规律: 一张桌子配6张凳子,每多一张桌子,桌子与桌子连接处少两张凳子。
6n-2(n-1)
…
规律:除第一张桌子配6张凳子,每多一张桌子,多4张凳子。
6+4(n-1)
…
…
…
规律:左右两边的两张桌子各配5张凳子,中间的桌子各配4张凳子。
4(n-2)+2×5
…
…
…
规律:每张桌子前后各4根凳子,左右各加一张凳子。
4n+2
…
…
…
按照上面桌凳的摆放方式,
寻找到的规律来完成下面表格:
桌子数 2 3 4 5 n
凳子数
10
14
18
22
4 n+2
…
…
3n+1
5n+2
火柴根数
火柴根数
1、用火柴棍拼接成如图所示的图形,请问拼接n 个这样的图形要多少根火柴?
n个
相信你一定能行的!
2、瓷砖拼图
4n+2
n块灰色瓷砖
白瓷砖块数
如图拼接瓷砖,如果用了n块灰色瓷砖,需要多少块白瓷砖
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
五、日 历 中 的 数 字 规 律
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
日历中每一横行相邻两个数之间有什麽关系?
答:右边的数比左边的数大1。
如果左边的数用a表示,则右边的数为 .
a+1
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
日历中每一竖列相邻两个数之间有什麽关系?
答:下边的数比上边的数大7。
如果上边的数用a表示,则下边的数为 .
a+7
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
从日历中任意框出3×3九个数,如果中间的一个数用a表示,你能根据刚才观察到的规律用含a的代数式表示出其余的几个数吗
a
a-8
a-7
a-6
a-1
a+1
a+6
a+7
a+8
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
(2)这个关系对其他这样的方框成立吗
(3)能不能用含字母的代数式表示这个规律呢
解:若用a表示中间这个数,则这9个数的和为___ .
9a
日 一 二 三 四 五 六
从日历中任意框出3×3九个数,这9个数之和可能为153吗 如果可能,请问这九个日期分别是几号?如果不可能,请说明理由.
日 一 二 三 四 五 六
9 10 11
16 17 18
23 24 25
从日历中任意框出3×3九个数,这9个数之和可能为153吗 如果可能,请问这九个日期分别是几号?如果不可能,请说明理由.
1、探索规律即根据题目的条件(包括有规律算式、图表、图形等信息),从简单或特殊情况入手,进行归纳,并大胆猜想探索,得出结论,再通过具体验证而获得规律的过程。
现阶段,虽然我们不能在理论上加以证明许多猜想,但我们可通过特例初步获得验证。
2、探索规律的一般步骤和方法
特殊入手
一般结论
个例验证
探索
观察思考分析交流
六、小结
寻找和探索规律是人类认识自然界和人类社会的重要环节,找到规律并按规律办事,不仅在数学上而且在人类社会的认识过程中都有非常重要的意义。
某校小食堂餐厅为长方形,
要安排70人同时就餐,请设计
一种桌椅摆放方案,使没有剩余桌椅(要求选用下列图中摆放方式)。请画出你满意的设计图。
1 只青蛙1 张嘴,2 只眼睛 4 条腿,扑通1 声跳下水;
2 只青蛙2 张嘴,4 只眼睛8 条腿,扑通2 声跳下水;
3 只青蛙3 张嘴,6 只眼睛12 条腿,扑通3 声跳下水;
n 只青蛙 张嘴, 只眼睛, 条腿,扑
通 声跳下水。
n
2n
4n
n
寻找和探索规律是人类认识自然界和社会的重要环节,找到规律并按规律办事,不仅在数学上而且在人类社会的认识过程中都有非常重要的意义。
二、细胞分裂问题
细胞每次都是由一个分裂成两个。
在有理数的乘方中我们曾经接触过“细胞分裂”问题:
想一想
1 个细胞 经过 n 次分裂,由1个能分裂成多少个?
分裂次数 1 2 3 4 … n
细胞个数
2
4
8
16
21
22
23
24
2n
…
模 型 “迁移”
你能否找到其它的类似的实际问题,使它与这个问题的条件与结论都对应相同吗?
议 一 议
〖模型1〗
将一根足够长的线段对折,求对折 n 次后线段的总条数。
( 2n条)
〖模型2〗
将一张白纸连续折叠,对折 n 次后的白纸总层数。
( 2n层)
三、折 纸 问 题
将一张白纸对折一次,如图所示折成两层,同时出现一条折痕;如果继续对折,使新折痕与上次的折痕保持平行,想一想,连续对折6次后可以折成多少层,出现几条折痕呢?
如果对折 10 次呢?
如果对折 n 次呢?
对折次数 1 2 3 4 … n
纸张层数
折痕数
2
4
8
16
21
22
23
24
2n
…
1
3
7
15
…
2n-1
按下面方式摆放桌凳:
一张桌子配6张凳子
两张桌子配 张凳子
你是怎么计算的?
10
按照这种方式继续摆桌凳,摆10张桌子配几
张凳子呢
…
…
…
摆100张桌子配几张凳子呢
1
6
2
10
3
14
4
18
5
22
凳子张数
桌子张数
10
42
…
…
…
…
100
402
?
规律: 一张桌子配6张凳子,每多一张桌子,桌子与桌子连接处少两张凳子。
6n-2(n-1)
…
规律:除第一张桌子配6张凳子,每多一张桌子,多4张凳子。
6+4(n-1)
…
…
…
规律:左右两边的两张桌子各配5张凳子,中间的桌子各配4张凳子。
4(n-2)+2×5
…
…
…
规律:每张桌子前后各4根凳子,左右各加一张凳子。
4n+2
…
…
…
按照上面桌凳的摆放方式,
寻找到的规律来完成下面表格:
桌子数 2 3 4 5 n
凳子数
10
14
18
22
4 n+2
…
…
3n+1
5n+2
火柴根数
火柴根数
1、用火柴棍拼接成如图所示的图形,请问拼接n 个这样的图形要多少根火柴?
n个
相信你一定能行的!
2、瓷砖拼图
4n+2
n块灰色瓷砖
白瓷砖块数
如图拼接瓷砖,如果用了n块灰色瓷砖,需要多少块白瓷砖
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
五、日 历 中 的 数 字 规 律
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
日历中每一横行相邻两个数之间有什麽关系?
答:右边的数比左边的数大1。
如果左边的数用a表示,则右边的数为 .
a+1
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
日历中每一竖列相邻两个数之间有什麽关系?
答:下边的数比上边的数大7。
如果上边的数用a表示,则下边的数为 .
a+7
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
从日历中任意框出3×3九个数,如果中间的一个数用a表示,你能根据刚才观察到的规律用含a的代数式表示出其余的几个数吗
a
a-8
a-7
a-6
a-1
a+1
a+6
a+7
a+8
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系
日 一 二 三 四 五 六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
(2)这个关系对其他这样的方框成立吗
(3)能不能用含字母的代数式表示这个规律呢
解:若用a表示中间这个数,则这9个数的和为___ .
9a
日 一 二 三 四 五 六
从日历中任意框出3×3九个数,这9个数之和可能为153吗 如果可能,请问这九个日期分别是几号?如果不可能,请说明理由.
日 一 二 三 四 五 六
9 10 11
16 17 18
23 24 25
从日历中任意框出3×3九个数,这9个数之和可能为153吗 如果可能,请问这九个日期分别是几号?如果不可能,请说明理由.
1、探索规律即根据题目的条件(包括有规律算式、图表、图形等信息),从简单或特殊情况入手,进行归纳,并大胆猜想探索,得出结论,再通过具体验证而获得规律的过程。
现阶段,虽然我们不能在理论上加以证明许多猜想,但我们可通过特例初步获得验证。
2、探索规律的一般步骤和方法
特殊入手
一般结论
个例验证
探索
观察思考分析交流
六、小结
寻找和探索规律是人类认识自然界和人类社会的重要环节,找到规律并按规律办事,不仅在数学上而且在人类社会的认识过程中都有非常重要的意义。
某校小食堂餐厅为长方形,
要安排70人同时就餐,请设计
一种桌椅摆放方案,使没有剩余桌椅(要求选用下列图中摆放方式)。请画出你满意的设计图。
